👨🏫 본 글은 칸 아카데미의 수업을 듣고 정리한 글 입니다.
- A more formal understanding of functions
- Vector transformations\
- Linear tranformation
- Matrix vector product as linear transformation
- Linear transformation as matrix vectors products
A more formal understanding of functions
🎈 이번 시간에는 함수에 대해 학습합니다.
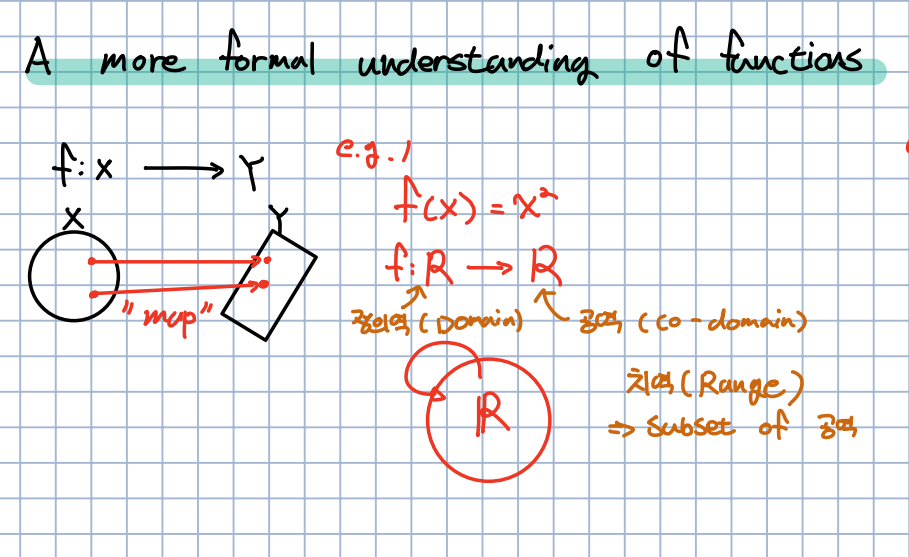
🎈 사실 대부분은 아는 내용이기 때문에 간단하게만 언급하고 넘어가겠습니다. 함수는 기본적으로 정의역, 공역 그리고 치역(공역의 부분집합)으로 이뤄져 있습니다.
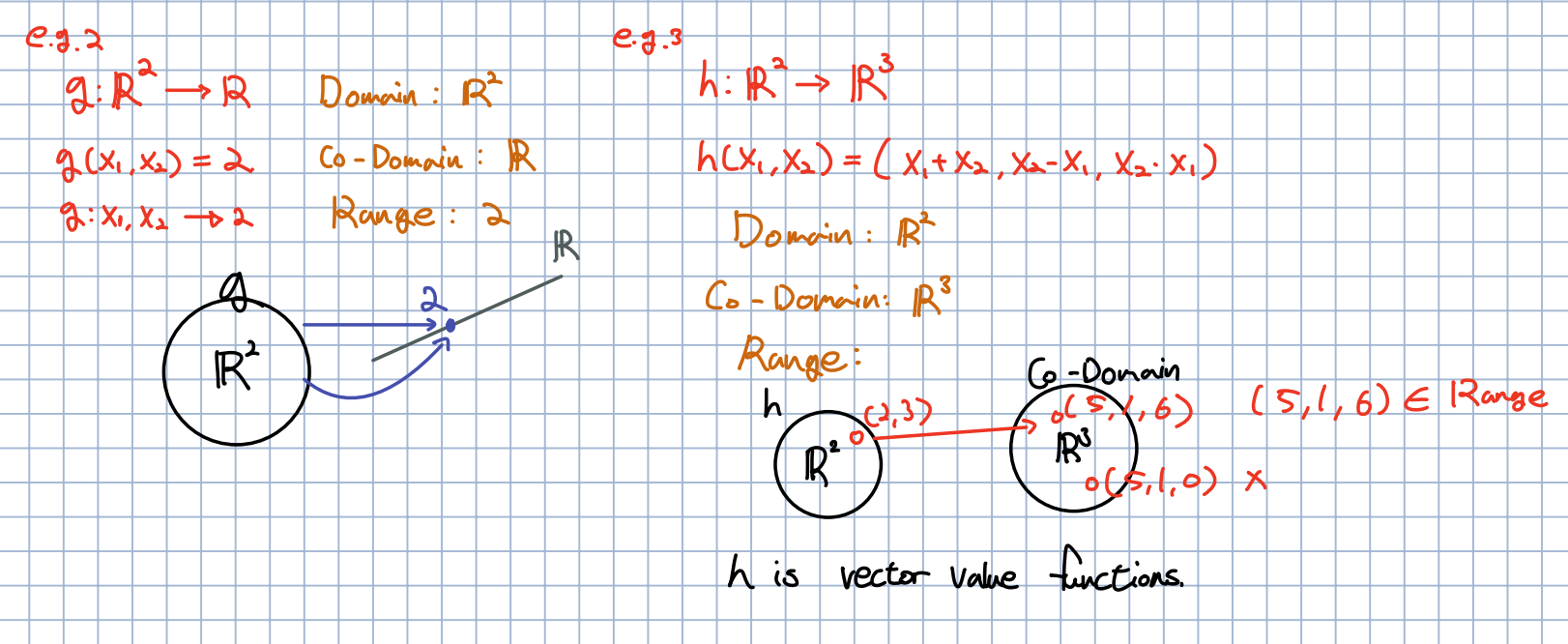
🎈 벡터 공간에서도 같은 이름으로 불리웁니다. 유일하게 다른 점은 다차원일 때의 함수를 vector value functions 이라고 부르는 것 입니다.
Vector transformations
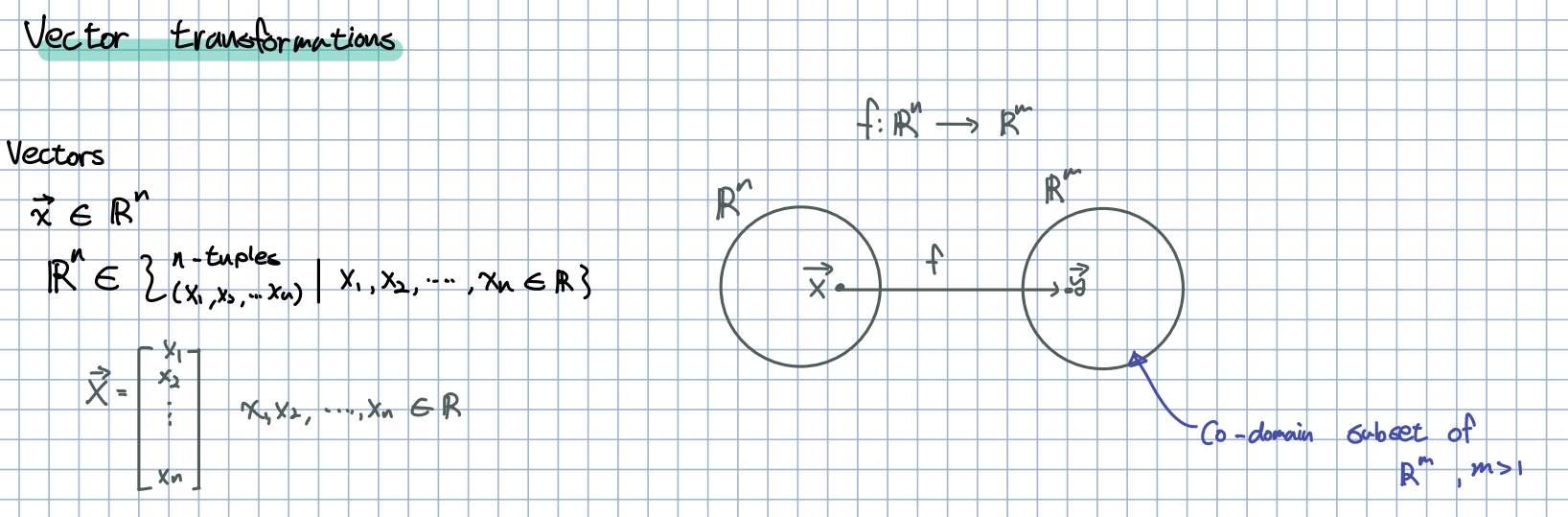
🎈 위는 벡터에 대한 함수를 말해주고 있습니다. 앞서서 한 내용의 또 다른 예시라고 말할 수 있습니다.

🎈 -> 으로 변환하는 함수에 대해 살펴보겠습니다. 이는 3차원 공간에서 2차원 공간으로 변환하는데, 벡터공간에서 우리는 이것을 Transformation(변환)이라고 불렀습니다. 그리고 변환은 함수와 같은 역활을 수행합니다. 단지 다차원의 공간일 뿐 역활을 똑같습니다.
Linear tranformation
🎈 이번 시간에는 선형 변환에 대해 학습합니다. AI를 공부하고 있는 저로썬 매우 중요한 개념이라고 생각됩니다.
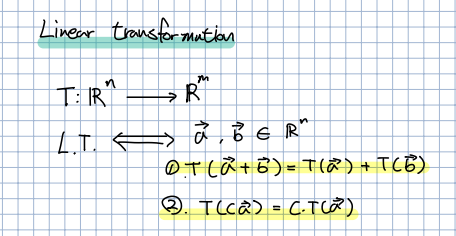
🎈 선형 변환이란 단순히 -> 으로 변환시키는 것은 아닙니다. 2가지의 필요충분조건을 만족해야합니다. 이는 "선형성"이라는 의미와 동일합니다. 위의 2가지 조건을 만족해야지만 이를 선형변환이라고 부를 수 있습니다.

🎈 위는 간단한 선형변환의 예시입니다. 위의 예제를 통해 가 선형변환을 만족하다는 것을 알 수 있습니다. 반례에 대해선 따로 필기하지 않았지만, 제곱이나 지수등등이 포함되어 있으면 만족하지 않습니다.
Matrix vector product as linear transformation
🎈 이번 강의에서는 행령곱 연산이 Linear Transformation임을 증명하는 수업입니다.
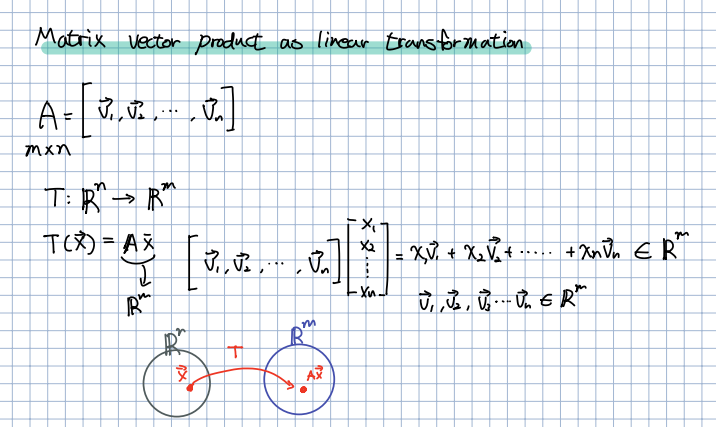
🎈 의 행렬 는 의 열벡터들로 이루어진 행렬이라고 정의합니다.
🎈 선형 변환 = 라고 정의할때 과연 이 함수는 선형변환의 정의를 만족하는지를 확인해보겠습니다.

🎈 선형 변환의 필요충분조건에는 2가지가 존재합니다. 가산성과 동차성을 만족해야합니다. 위의 두 과정은 바로 2개의 조건에 대해 만족하는 증명하는 과정입니다. 결과적으로는 만족하다는 것을 알 수 있습니다. 다시 이야기 하면 행렬곱은 선형 변환이라고 말할 수 있습니다.
Linear transformation as matrix vectors products
🎈 이번 시간에는 단위 행렬과 선형 변환의 관계를 학습합니다.

🎈 먼저 단위행렬()에 대해 정의합니다. 단위 행렬은 대각성분이 모두 1인 행렬을 의미합니다. 또한 임의의 벡터와의 product 연산 시 해가 임의의 벡터라는 매우 중요한 성질을 가지고 있습니다(일반적으로 1이라고 생각할 수 있습니다).
🎈 단위 행렬의 열벡터를 ... 를 standard basis for (표준기반벡터)라고 부릅니다. 그렇다면 우리는 임의의 들을 단위 행렬과의 선형 결합으로 표현할 수 있습니다.
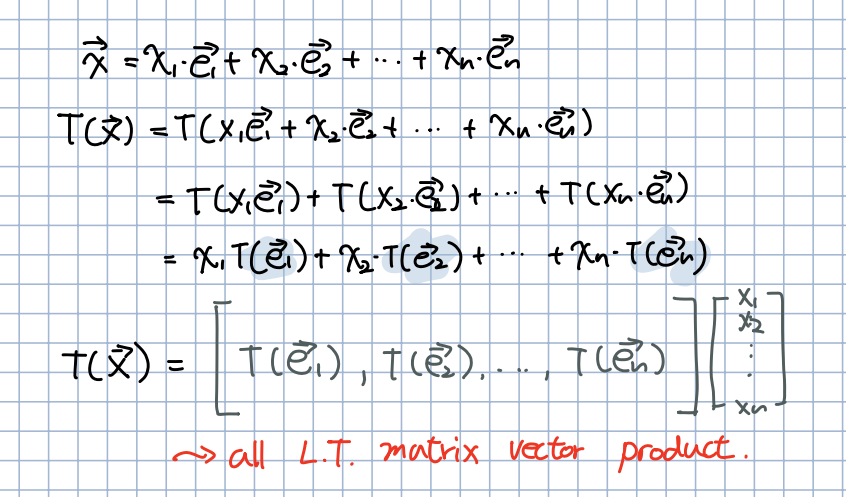
🎈 단위 벡터의 선형결합으로 이루어진 를 선형변환한다면, 선형변환의 필요충분조건을 사용해 선형변환의 곱으로 이루어진 단위벡터와 의 product연산을 확인 할 수 있습니다.
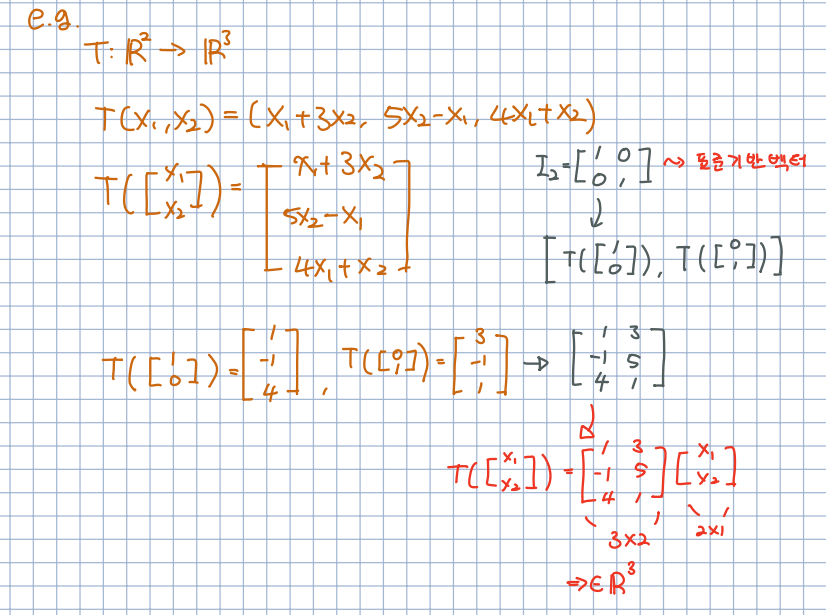
🎈 이러한 단위백터의 특징을 사용하면 선형변환의 식을 더욱 보기 쉽게 표현할 수 있습니다.
