👨‍🏫 본 리뷰는 cs231n-2017 강의를 바탕으로 진행했습니다.

Syllabus
Youtube Link

Backpropagation

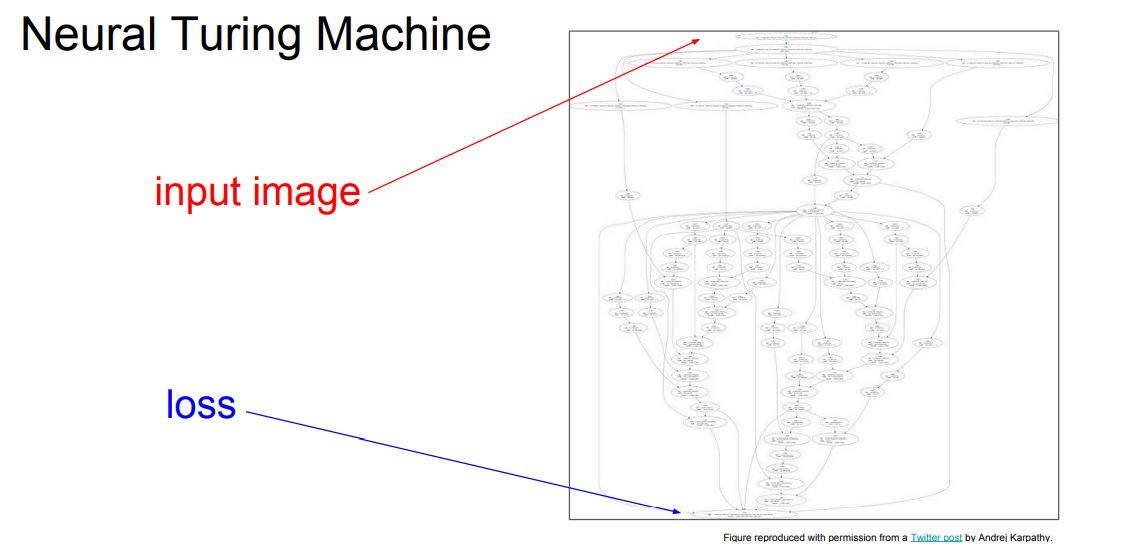
📌 전 강의들에서 다양한 Loss function과 Reqularzation 그리고 Optimazation에 대해서 학습했습니다. 이번 시간에는 역전파(Backpropagation)에 대해 학습하도록 하겠습니다.

📌 위의 그림은 우리가 지금까지 배웠던 Neural Network의 구조를 더욱 깊이한, 조금 더 실제 딥러닝 네트워크에 가까운 그림입니다. input image부터 loss까지 연산 깊이가 너무나도 깊습니다. 일반적으로 input image에서 loss까지의 연산을 순전파라고 합니다. 역전파는 이름 그대로 반대로 하는 연산입니다.

📌 역전파가 왜 필요할까요? 우리는 gradient를 통해 optimization을 해야합니다. gradient 계산을 하기 위해선 당연하게도 미분 값이 필요합니다. 하지만 위의 사진을 볼 수 있듯이 loss를 구한 후 다시 각각의 미분 값을 구하는건 너무나도 비효율적입니다. 그래서 우린 연쇄법칙(Chain Rule)을 이용한 역전파 연산을 통해 효율적으로 미분 값을 계산 할 수 있습니다.

📌 위의 각각의 $x$, $y$, $z$와 간단한 연산을 사용한 역전파 예제입니다. 초록색으로 있는 부분은 순전파 연산의 결과입니다. 우리는 이제부터 역전파 연산을 진행합니다. 먼저 $\partial f\over\partial f$ 자기 자신을 미분합니다. 당연히 결과는 1 입니다.

📌 다음으로 $\partial f\over\partial z$로 미분합니다. 위의 reference에서 친절하게 $q$(=3)라고 알려줍니다.

📌 다음으로 $\partial f\over\partial q$로 미분합니다. 역시나 reference에서 친절하게 $z$(=-4)라고 알려줍니다.

📌 이제부터 연쇄법칙(chain rule)을 사용해 연산을 진행합니다. 우리가 계산하고자 하는 미분 연산은 $\partial f\over\partial y$ 입니다. 우리는 위의 사진의 Chain rule을 사용해 연산합니다. Chain rule을 사용하는 이유는 우리는 앞선 계산에서의 미분 값을 알기 때문에 자기 주변의 local에 대한 미분만을 계산한 후 연산하면 되기 때문입니다. $+$ 연산에 대한 미분은 1이기 때문에 그대로 -4가 나옵니다. 나머지 $x$ 또한 동일한 방법으로 진행됩니다.

📌 위의 사진과 같이 "local gradient"만 알 수 있다면, 앞선(upstream)의 미분 값으로 Chain rule을 사용해 쉽게 미분 연산을 진행할 수 있습니다. 우리는 순전파 연산에서 각각의 값만 저장해 놓는다면 역전파 연산을 통해 쉽게 grediant를 계산할 수 있습니다.

📌 위의 사진은 sigmode function(non-linear)을 사용한 조금 더 복잡한 역전파 계산입니다. 하나씩 천천히 연산을 진행하면 각각의 값을 계산할 수 있습니다.

Q. What is a max gate ?

📌 위의 max gate는 어떤 역활을 할까요? 위의 사진에서는 gradient router 라고 표현합니다. 순전파로 진행되는 max 연산을 생각해보면 max값을 제외만 나머지 값은 연산에 영향을 주지 않습니다. 그렇기에 역전파 과정에서도 영향을 준 노드에게만 흘러갑니다.

Q. What is a mul gate ?

📌 위의 mul gate는 gradient switcher라고 표현합니다. 역전파 흐름을 잘 보면 각각의 반대의 값을 곱한 값이 흐르는 것을 볼 수 있습니다.

Q. What is the size Jacobain matrix?

📌 사실 우린 스칼라 값을 다루는 것이아니라, 백터 연산을 합니다. 우린 자코비안 행렬을 사용해 실제로 연산을 진행합니다.(자코비안 행렬에 관련 링크 입니다.) 4096개의 vector를 input 넣으면 [4096 x 4096]의 행렬을 이루고 있을겁니다.

📌 지금부터는 벡터를 사용한 예제에 대해 학습할 것입니다. 벡터에 대한 순전파 연산을 진행합니다. 그리고 우리는 L2 Norm을 사용했기에 $\partial f\over\partial q_i$ = $2q_i$ 결과를 얻을 수 있습니다.

📌 이어서 역전파 연산을 진행합니다. W에 대한 미분 연산을 진행합니다. $\triangledown wf = 2q*x^T$ 의 연산을 진행합니다. 각각의 연산을 수행해보면 $0.088 = 0.2* 0.44$, $0.176 = 0.4* 0.44$, $0.104 = 0.2* 0.52$, $0.208 = 0.4* 0.52$ 연산을 수행합니다. 또한 gradient와 가중치의 shape은 항상 일치해야합니다.

📌 $x$에 대한 미분 연산을 또한 진행합니다. $\triangledown xf = 2W^T*q$ 의 연산을 수행합니다. 각각의 연산을 진행해보면 $-0.112=0.1*0.44 - 0.3*0.52$, $0.636=0.5*0.44 - 0.8*0.52$ 연산을 수행합니다.

📌 Multiply Gate 예시 코드입니다. forward시 각각의 변수를 따로 저장합니다. backward시 저장한 변수를 사용해 연산을 진행합니다.