Kaggle

https://www.kaggle.com/competitions/optiver-realized-volatility-prediction

Code From

https://www.kaggle.com/competitions/optiver-realized-volatility-prediction/discussion/274970

Overview

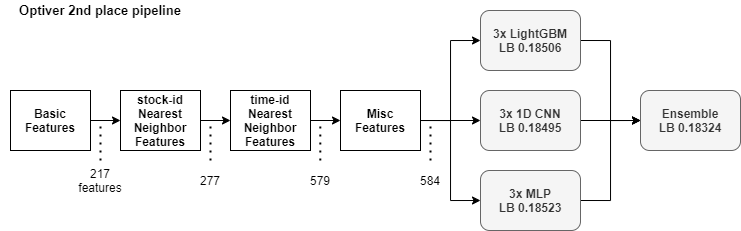
Feature Engineering

book data와 trade data를 하나의 Dataframe으로 합치는 과정
두 dataset에서 하나의 time_id를 기준으로, 각각의 파생된 데이터를 생성 후, 하나의 Dataframe으로 합침

하나의 time_id의 seconds_in_bucket의 개수가 각각 다르므로,
count, log_return, sum, mean, std, realized_volatility의 특성으로 함축시킴

Basic Features

book data (호가 정보)

• time_id

• seconds_in_bucket

• bid_price1

• ask_price1

• bid_price2

• ask_price2

• bid_size1

• ask_size1

• bid_size2

• ask_size2

trade data (거래 정보)

• time_id

• seconds_in_bucket

• price

• size : 거래량

• order_count : 거래 주문 수?

Derived Feature

From Book data

• book.seconds_in_bucket.count
• book.wap1
• book.wap2
• book.log_return1
• book.log_return2
• book.log_return_ask1
• book.log_return_ask2
• book.log_return_bid1
• book.log_return_bid2
• book.wap_balance : abs(wap1 - wap2)
• book.price_spread
• book.bid_spread
• book.ask_spread
• book.total_volume
• book.volume_imbalance

• book_450
  ... 위와 동일
• book_300
  ... 위와 동일
• book_150
  ... 위와 동일

From Trade data

• trade.log_return.realized_volatility

• trade.seconds_in_bucket.count

• trade.size.sum

• trade.order_count.mean

• trade_450
  ... 위와 동일
  

• trade_300
  ... 위와 동일

• trade_150
  ... 위와 동일

• tick_size

Question

기존 정보에서 파생된 데이터들 또한 결국 수학 수식에 의해 결정된 것이기에 Derived Feature가 유의미한가??

450 300 150 3개만 나눈 이유는??

Answer

=> count, log_return, sum, mean, std, realized_volatility의 특성으로 함축시킴

=> 이미 전체 데이터에 포함 되어 있고, 너무 과거의 데이터는 큰 의미가 없기 때문에??

Nearest-Neighbor Features

GBDT 모델에 직접으로 들어가는 Feature는 아니지만, Nearest-Neighbor Features를 추가하기 위해 tau feature를 생성

• price : 0.01 / df['tick_size']
  time id의 변화 마다 tick size(ask2 - ask1) 의 변화의 역수?
• vol : df['book.log_return1.realized_volatility']
• trade.tau : np.sqrt(1 / df['trade.seconds_in_bucket.count'])
• trade.size.sum : df['book.total_volume.sum']

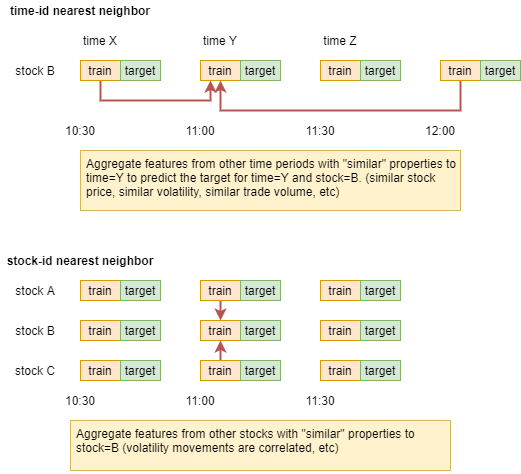
Build Nearest Neighbors

Logic

index='time_id', columns='stock_id', values='feature_col'인
pivot table에서 각 80개 Neighbors Search

• Pivot table의 Nan 값은 기준 열의 평균 값으로 치환
• 모든 Pivot table은 min max scaling이 적용
• Pivot table이 time_id 기준이므로, stock_id 기준으로 계산 시
  Transpose 필요

Price

time_price_c
Metric : Canberra

time_price_m
Metric : Mahalanobis (공적분)

stock_price_l1 (min max scaling 후, transpose)
Metric : minkowski (Default)

Volatility

time_vol_l1
Metric : minkowski (Default)

stock_vol_l1 (min max scaling 후, transpose)
Metric : minkowski (Default)

Size (Volume)

time_size_m
Metric : Canberra

time_size_c
Metric : Mahalanobis (공적분)

Question

Canberra, Mahalanobis, minkowski 각각의 방법이 시계열 분석에 어떤 의미가 있는지 알 필요가 있을 것 같음.

calculate_rank_correraltion

지난 번 미팅 때, 확인한 Rank correraltion은 Top 5의 Rank 만 비교한 것이고, Top 10개로 늘려서 확인해 본 결과 상관계수가 더 줄어들었음.

위에서 추출한 특성들이 큰 상관관계가 없다는 것은 모델 학습에 이점이라고 생각이 가능하나, 해당 상관관계는 Rank 값을 나열한 Table로 correraltion은 계산한 것이기에 상관계수가 낮게 나오는 것이 당연하다고 생각함.

Logic

neighbors table을 쭉 펼친 후 (3833 x 10) -> (38330) 각 테이블마다의 상관계수 계산

그렇다면 찾아낸 Nearest-Neighbor Features들을 어떻게 dataframe의 특성으로 추출해 낼 것인가??

Aggregate Features With Neighbors

Rank NORMALIZATION

default : high value high rank
시계열 데이터에서는 특정 특징이 시간이 지남에 따라 크게 변하는 경우
변동이 큰 특징을 상대적인 순위로 변환해 특징 값의 절대적인 크기가 아닌, 해당 시간 단위에서의 상대적인 위치와 비교 가능한 정보로 변환

LSTM이나 Advanced된 모델을 사용하게 되면 Rank Scaling이 큰 의미가 있을지는 의문

make_nearest_neighbor_feature

위에서 말한 "그렇다면 찾아낸 Nearest-Neighbor Features들을 어떻게 dataframe의 특성으로 추출해 낼 것인가??" 에 대한 답

해당 과정은 크게 두 가지인 rearrange와 make_nn_feature 과정으로 나뉜다.

Rearrange 과정은 knn에서 추출한 neighbor index를 토대로 feature_pivot (pivot table)를 Rearrange 하는 과정인데,
전체적인 값은 같지만 feature_value (pivot table) 내부 값의 위치만 달라진다. 이러한 방식으로 80개의 feature_pivot [3833,112]를 가진
feature_value [80,3833,112]를 생성한다.

make_nn_feature 과정은 80개의 table 중 n개의 table를 sum, mean, std 등의 값으로 추출해 하나의 특성 추출한다.

Misc Features

Log Scaling

miscellaneous Features = 잡다한 특징

skew correction for NN : 거래량은 일정하지 않고 크게 튀는 성질을 가지고 있어 log scaling을 하였음.

cols_to_log = [
    'trade.size.sum',
    'trade_150.size.sum',
    'trade_300.size.sum',
    'trade_450.size.sum',
    'volume_imbalance'
]

EMA Realized_Volatility

'book.log_return1.realized_volatility'를 window 3~10의 size로 이동평균 Feature를 생성

EMA 이긴 한데, 주변과 비슷한 값과 맞추어 평균화하는 작업으로 큰 의미가 있어보이지는 않고, time order가 맞추어지지 않은 상황에서 한 EMA라 전처리 시간만 낭비되는 것 같다고 생각함.