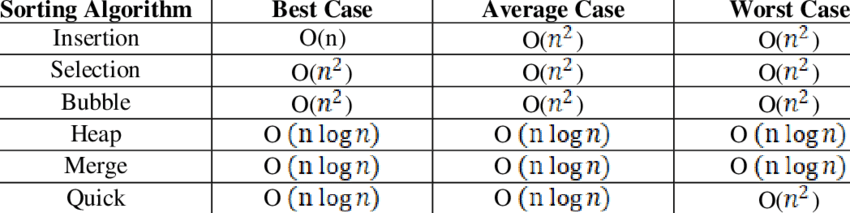
Sorting Algorithms | Time Complexity, Recurrence relation

Bubble Sort

Recurrence Relation

$T(n) = T(n-1) + \Theta(n)$

Insertion Sort

Recurrence Relation

Worst

$T(n) = T(n-1) + \Theta(n)$

Best

$T(n) = T(n-1) + \Theta(1)$

Selection Sort

Recurrence Relation

All Case

$T(n) = T(n-1) + \Theta(n)$

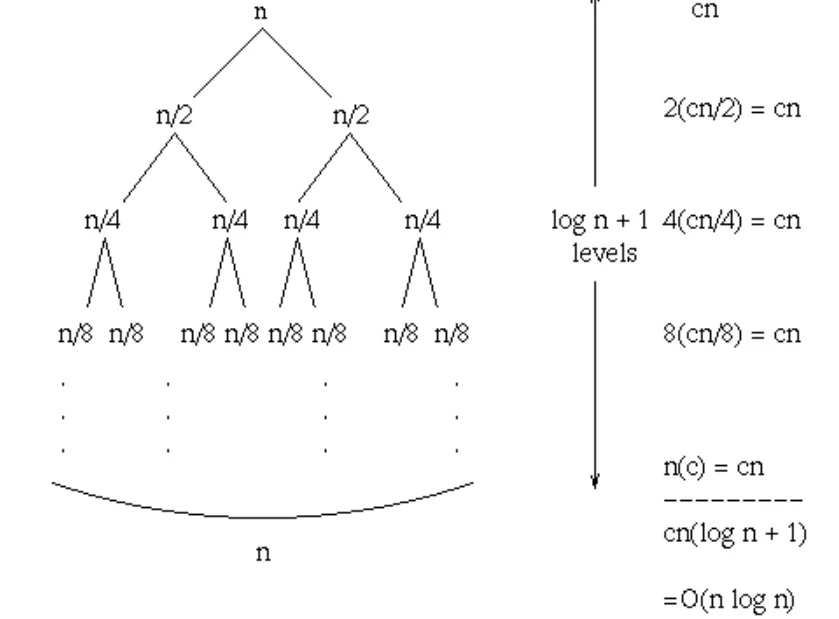
Merge Sort

Recurrence Relation

All Case

$T(n) = 2T\left(\frac{n}{2}\right) + \Theta(n)$

Heap Sort

Recurrence Relation

All Case

$T(n) = T(n-1) + \Theta(\log n)$

Quick Sort

Recurrence Relation

Average / Best

$T(n) = 2T\left(\frac{n}{2}\right) + \Theta(n)$

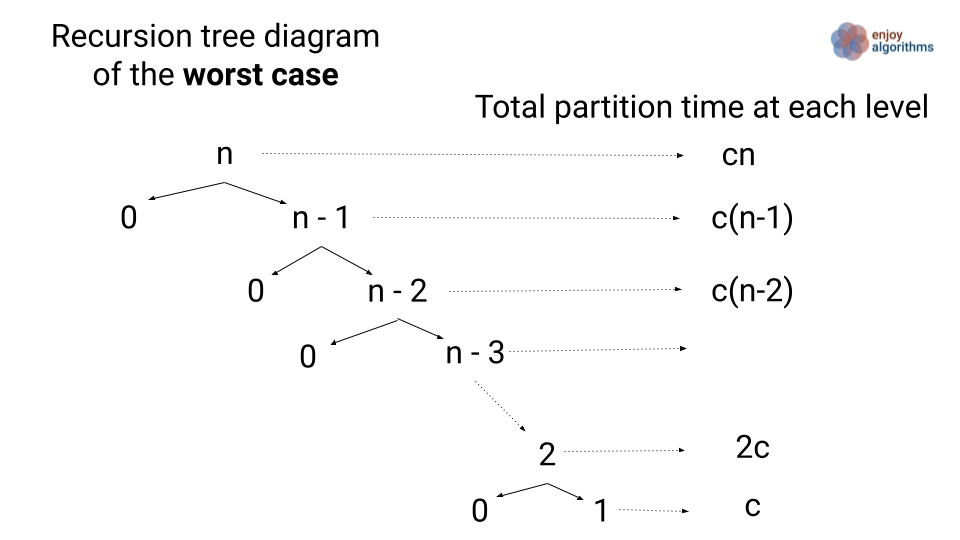
Worst

$T(n) = T(n-1) + \Theta(n)$