5.7 Application to Differential Equations

6.1 Inner Product, Lengh, and Orthogonality

• 내적 의미
• 벡터 성질 4가지
• 벡터 길이
• 벡터 간 거리
• 직교 벡터 성질
• 피타고라스 정리
• Orthogonal Complements
• Nul A

Refer

6.2 Orthogonal Sets

• Orthogonal Sets
• Orthogonal basis
• Orthogonal Projection
• Orthonormal Sets
• U^T * U = I

6.3 Orthogonal Projection

• Orthogonal Decomposition - Orthonormal basis : projwY = UU^Ty

Refer

6.4 The Gram-Schmidt Process

• Gram-Schmidt process
• Orthonormal basis
• QR Factorization of Matrices

Refer

6.5 Least-Squares Probelms

• 25 (True) : the normal equations always provide a reliable method for computing least-squares solutions.
  Normal Equation은 항상 해가 있기 때문

• 26 (True) :
  

• 27

Refer

6.6

Refer

6.7

Refer

7.1

7.2

• x=0을 제외한 모든 Q(x)가 양수이면 positive definite
• x=0을 제외한 모든 Q(x)가 음수이면 negative definite
• Q(x)가 양수와 음수 모두 지니고 있으면 indefinite
• 모든 x에 대해 Q(x)가 0이상이면 positive semidefinite
• 모든 x에 대해 Q(x)가 0 이하이면 negative semidefinite

7.3

7.4

Misstakes

• 백터, Matrix 연산 실수

• the least squares error는 예측 값과 실제 값의 수직거리 합
  

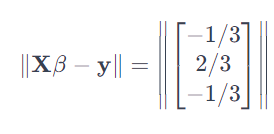
• Spectral Decomposition of A
  $A = \lambda_1 \mathbf{v}_1 \mathbf{v}_1^\top + \lambda_2 \mathbf{v}_2 \mathbf{v}_2^\top$

• indefinite , positive finite, negative finite

• Q(x) 에서의 최댓값은 Eigen Value 이고, 최댓값에서의 백터는 Vector의 음수 양수 둘 다