1.9

The Matrix of a Linear Transformation

• onto : R^n -> R^m 했을 때, R^n이 R^m 상에 꽉 차야함
• one to one

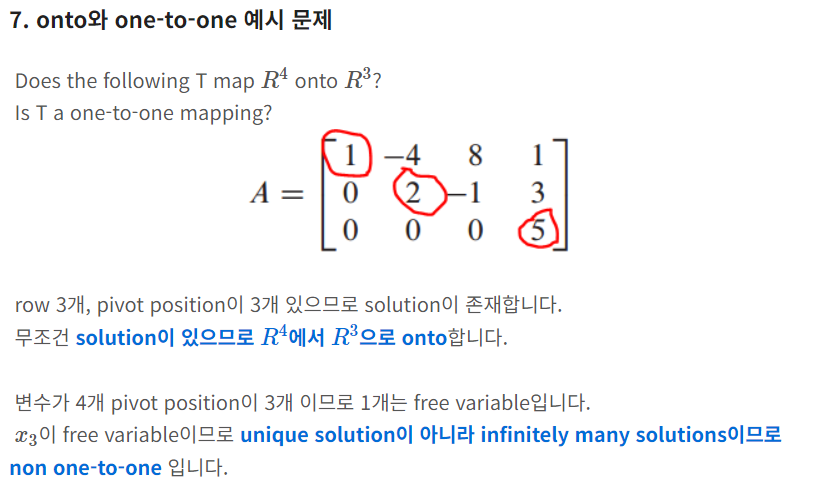
onto 판단 문제

T (m x n)에서 pivot의 개수가 이미지의 Rank와 동일해야 함 -> 이미지에서의 해가 존재

one to one 판단 문제

free variable이 있음 -> Ax = b를 만족하는 x가 여러 개 -> not one to one

2.3

Characterizations of Invertible Matirces

• 역행렬 이론 (역행렬 만족 조건들)
• invertible 정의
• T가 invertible이면 A(standard matrix)도 invertible

주어진 행렬이 Invertible 한지 판단

• Ax = 0이 trivialsolution 만을 가져 independent
• n개의 pivot을 가지는지 (one-to-one)
• A는 solution이 있으므로 A는 R공간에 span (onto)

2.4

Partitioned Matrices

• 분할 행렬 or 블록 행렬 - Partitioned Matrix or Block Matrix
• 분할 행렬의 덧셈과 스칼라 곱 - Addition and Scalar Multiplication
• 분할 행렬의 곱 - Multiplication of Partitioned Matrix
• AB의 열-행 확장 - Column-Row Expansion of AB
• 분할 행렬의 역행렬 - Inverses of Partitioned Matrix

분할행렬 사용해 역행렬 구하기

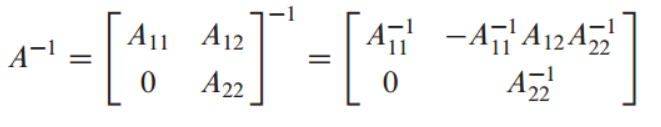
2.5

Matrix Factorizations

• Factorization, decomposition
• LU 분해 - LU decomposition (공식 !!)
• LU 분해의 유용성
• LU 분해 문제

주어진 행렬 A -> LU 분해

직렬 병렬 회로 문제

2.7

Applications to Computer Graphics

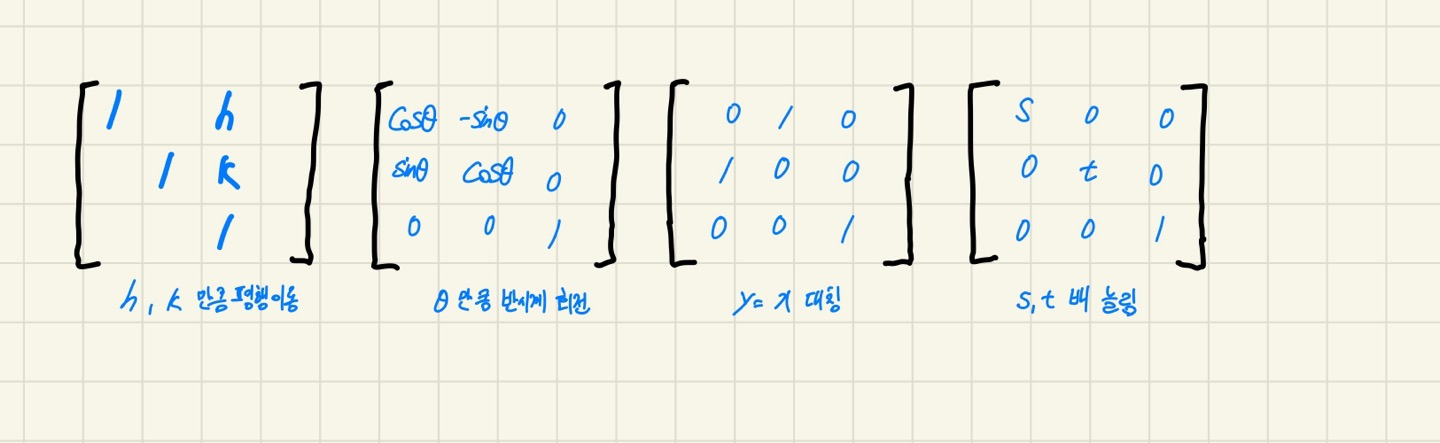
평행이동, 회전, 대칭이동, scale 문제

2.8

Subspaces of Rn

• Rn 공간에서의 부분공간 H 정의 조건
• 열 공간 - Column Space
• null space
• 부분공간에서 기저 - Basis for a Subspace
• Rn 공간에서 표준 기저 - Standard Basis for Rn

열 공간 A에 b가 존재하는지 문제

• Ax = b 의 해가 있는지만 찾으면 됨 (consistent)

영 공간에 대한 기저 찾기 문제

• Ax = 0의 solution을 구하고
• general solution으로 표현
  

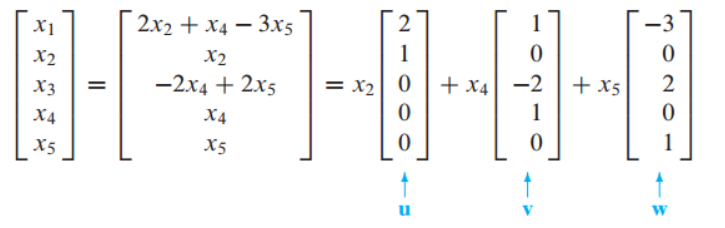
열 공간에 대한 기저 찾기 문제

2.9

Demension & Rank

• 부분공간에서의 기저
• H의 vector는 basis vector의 linear combination으로 표현
• Coordinate Vector
• Demension 정의
• Rank 정의

Coordinate Vector 표현 문제

3.1

Introduction to Determinant

• 행렬식 : determinant (공식!!)
• 여인수 : cofactor
• 여인수 전개 : cofactor expansion
• triangular matrix determinant
• det EA = (detE) (detA)

- cofactor expansion (5x5 matrix 행렬, easy zero)

3.2

Properties of Determinants

• det A = 0이 아니면 A는 invertible
• A^T의 det과 det A는 동일
• det AB = (det A)(det B)

Row Operations 시 det 값 문제 (triangular matrix det 이용)

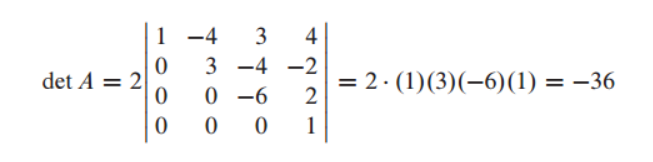
3.3

Cramer's Rule, Volume, Linear Transformations

• 크래머의 법칙 (공식!!)
• 크래머 법칙을 사용한 역행렬 구하기