Join Operation

DB환경에서 조인연산을 구현하는 방법은 크게 3가지로 나눌 수 있다.

• Nested-loop join : 반복문을 돌면서 조인
• Merge join : 테이블을 정렬한 뒤 조인
• Hash join : 해시함수를 사용하여 조인

이 중 Nested-loop join과 Merge join은 버퍼에 최소 3페이지(Table1, Table2, Result)만 할당되어도 사용할 수 있지만, Hash join의 경우 버퍼에 할당된 페이지의 수가 많을 때 사용 가능한 방법이다.

이후 소개할 모든 알고리즘에서는 다음 테이블과 sql문을 예시로 사용한다.

table	student	takes
records	5,000	10,000
blocks	100	400
BF	50	25

select *
from student S, takes T
where S.id = T.id

Nested-loop Join

Nested-loop Join은 릴레이션의 모든 튜플에 대해 모든 조합을 검사하는 방식으로, 이중 반복문을 통해 구현된다.

Nested-loop Join은 외부릴레이션의 모든 레코드에 대해 내부 릴레이션의 모든 블록을 메모리에 올려 확인하기 때문에 비용식은 아래와 같이 계산된다.

Nested-loop Join(Worst case): Cost = n * bs + br (외부 테이블 레코드 수 * 내부 테이블 블록 수 + 외부 테이블 블록 수)
Nested-loop Join(Best case): Cost = bs + br (내부 테이블 블록 수 + 외부 테이블 블록 수)

위의 비용식에서 Best case는 버퍼에 할당됭 페이지 수가 내부테이블의 블록 수 + 2보다 같거나클 때(M >= bs + 2)적용 가능한 방법으로, 내부 테이블의 모든 블록을 버퍼에 올려놓은 상태에서 외부 테이블을 한 블록씩 버퍼에 올리면서 조인을 수행한다. 이때 두 테이블 중 레코드의 수가 더 적은 테이블을 내부 테이블로 사용한다.

앞의 예시에서 Nested-loop Join방식을 채택한다면 비용은 다음과 같다.

• Worst case
  • outer relation이 student일 때 : Cost = 5,000 * 400 + 100 = 2,000,100
  • outer relation이 takes일 때 : Cost = 10,000 * 100 + 400 = 1,000,400
• Best case : Cost = 400 + 100 = 500

이 방법은 모든 레코드를 비교하기 때문에 어떤 조인 조건이든 사용할 수 있다는 장점이 있지만, 비용이 매우 크다는 단점이 있다.

Block Nested-loop Join

Block Nested-loop Join은 Nested-loop Join을 개선시킨 방법으로, 외부 테이블의 모든 레코드에 대해서 반복을 수행하는 것이 아니라, 외부 테이블의 블록에 대해서 내부 테이블을 비교하는 방법이다. 즉, 외부 테이블의 각 블록에 대해서 내부 테이블의 블록을 한번씩만 검사하는 방법이다.

슈도코드상으로는 총 4중 반복문이 돌기 때문에 더 비효율적으로 보이지만, DB의 관점에서 레코드당 블록 I/O가 발생하던게 블록당 I/O가 발생하는 것으로 줄어들었기 때문에 좀 더 적은 비용으로 작업을 처리할 수 있다.

Block Nested-loop Join의 비용식은 Worst case와 Best case 각각 다음과 같이 계산된다. 이전 방법과 동일하게 Worst case는 버퍼에 3개의 블록만 할당된 경우이고, Best case는 버퍼에 내부테이블 전체를 올려서 연산을 수행하는 경우이다.

Block Nested-loop Join(Worst case): Cost = br * bs + br (외부 테이블 블록 수 * 내부 테이블 블록 수 + 외부 테이블 블록 수)
Block Nested-loop Join(Best case): Cost = bs + br (내부 테이블 블록 수 + 외부 테이블 블록 수)

이 식을 좀 더 일반화하면 다음과 같이 작성할 수 있다.

Block Nested-loop Join: Cost = x * bs + br = ceil(br / (M-2)) * bs + br (내부 테이블 스캔 횟수 + 외부 테이블 스캔 횟수)

식을 해석하면, 내부 테이블의 스캔 횟수는 내부 테이블의 블록 수에 x를 곱해서 구할 수 있는데, x는 버퍼에 한번에 올라올 수 있는 블록의 수로, 외부 테이블의 전체 블록수(br)에서 버퍼에 할당된 페이지 수(M)중 내부 테이블과 결과 페이지를 제외한 만큼(M-2)을 나눠서 구할 수 있다.(x = br / M-2)

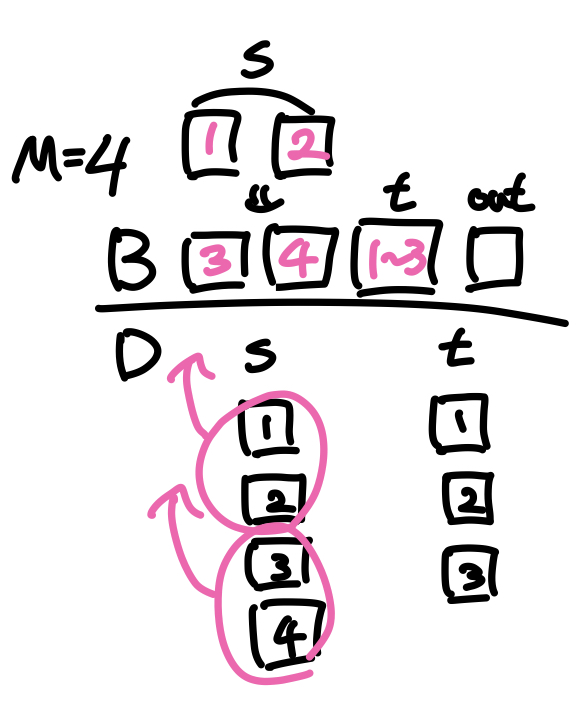
즉, (Block) Nested-loop join방식의 비용은 내부 테이블을 스캔하는 횟수와 외부 테이블을 스캔하는 횟수의 합으로 구할 수 있는데, 일반 Nested-loop의 경우 x = n(외부 테이블의 레코드 수)인 경우이고, Block Nested-loop방식은 x = ceil(br / M-2)(한번에 올릴 수 있는 블록 수)인 경우이다.

앞의 예시에서 Block Nested-loop Join방식을 채택한다면 비용은 다음과 같다.

• Worst case
  • outer relation이 student일 때 : Cost = 100 * 400 + 100 = 40,100
  • outer relation이 takes일 때 : Cost = 400 * 100 + 400 = 40,400
• Best case : Cost = 400 + 100 = 500

Indexed Nested-loop Join

Nested-loop Join에서 내부 테이블 전체를 스캔하는 것 대신 인덱스를 사용하면 비용을 조금 더 줄일 수 있는데, 이를 Indexed Nested-loop Join이라고 한다.

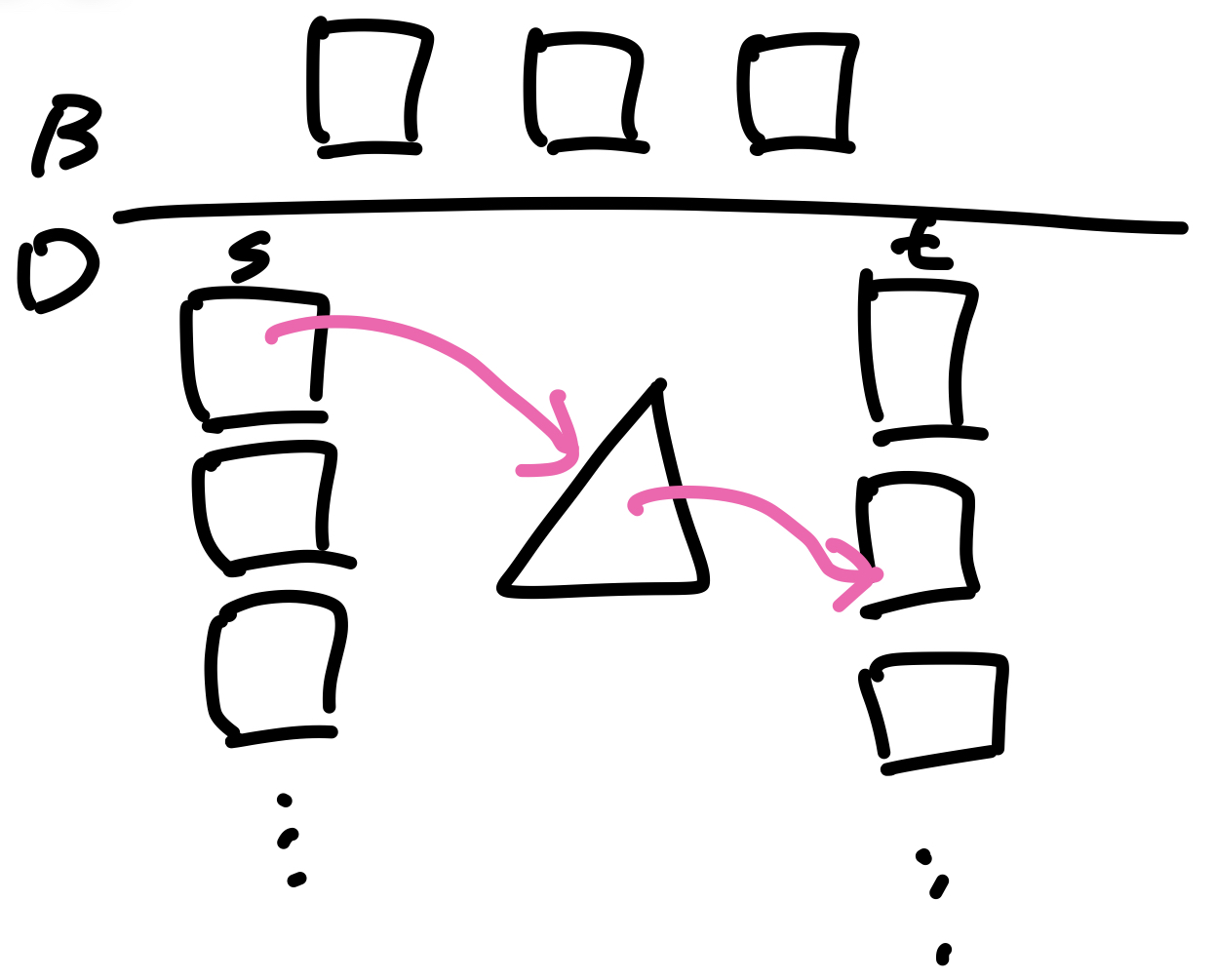
이 방법은 내부 테이블의 attribute에 인덱스를 설정하여 인덱스를 통해 조건에 맞는 레코드를 찾은 뒤 해당 블록만 버퍼에 올려 작업하는 방법으로, 비용식은 다음과 같다.

Indexed Nested-loop Join: Cost = n * c + br (외부 테이블 레코드 수 * 레코드당 인덱스 탐색 및 결과 블록 I/O횟수 + 외부 테이블 블록 수)

위 식에서 n * c는 내부 테이블의 블록을 I/O하는 횟수로 n은 외부 테이블의 레코드 수, c는 레코드당 인덱스를 탐색하고 결과로 나온 블록을 I/O하는 횟수이다.

인덱스로 B+트리를 사용하고 트리의 높이가 4일 때, student와 takes를 조인하는 비용은 다음과 같다.

• Cost = 5000 * 5 + 100 = 25,100 (5 = 4(트리 높이) + 1(평균 결과 블록))

Merge Join

(Sort)Merge Join은 두 테이블이 join attirbute에 대해 정렬이 되어있다는 가정하에 출발한다. 만약 정렬이 되어있지 않다면 두 테이블을 정렬하고, 두 테이블의 맨 첫 레코드부터 포인터를 하나씩 이동하며 레코드를 비교하면서, join attribute값이 같은 레코드들을 결과 페이지로 복사하는 방식으로 조인 연산을 수행한다. 이때, 양쪽 테이블이 같은 컬럼을 기준으로 정렬되어있기 때문에 전체 테이블을 한번씩 스캔하는 것 만으로도 연산이 가능하다.(one pass join)

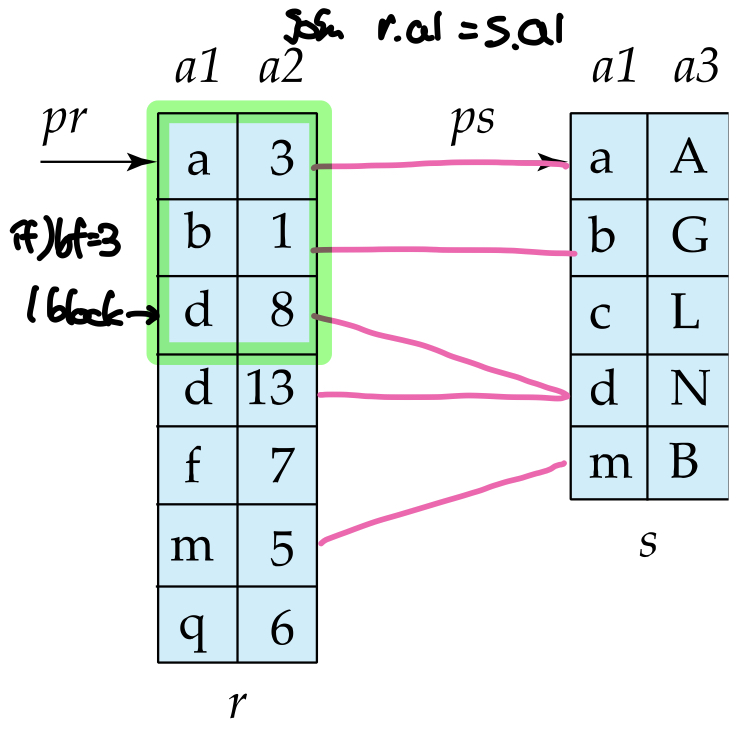
Merge Join은 양쪽 테이블을 한번씩 스캔하면 연산이 끝나기 때문에 비용은 두 테이블의 블록 수의 합이 된다. 하지만 테이블이 정렬되지 않은 경우 두 테이블을 정렬하는 비용까지 포함되기 때문에 최종적인 비용식은 아래와 같다.

Merge Join(Sorted) : Cost = br + bs + Sorting Cost (외부 테이블 블록 수 + 내부 테이블 블록 수 + 정렬 비용)

여기에서 정렬 알고리즘은 External Sorting을 사용하는데, 정렬을 중간연산으로 사용하기 때문에 결과를 디스크에 쓰는 작업을 포함하여 비용식을 계산한다.

• Sorting Cost = 2b(ceil(logM-1(b/M)) + 1)

또한 두 테이블 모두 정렬되어야 하기 때문에 각 테이블에 대한 정렬비용이 추가된다.

Merge Join에서는 외부정렬을 사용하기 때문에 버퍼 페이지의 수에 따라 비용이 달라진다. 위의 예시의 조인 비용을 계산하면 다음과 같다.

• Merge join cost(M = 3)
  = takes table sorting cost + student table sorting cost + join cost
  = 2 * 400(log2(400 / 3) + 1) + 2 * 100(log2(100 / 3) + 1) + (100 + 400)
  = 7200 + 1400 + 500
  = 9100

• Merge join cost(M = 25)
  = takes table sorting cost + student table sorting cost + join cost
  = 2 * 400(log24(400 / 3) + 1) + 2 * 100(log24(100 / 3) + 1) + (100 + 400)
  = 1600 + 400 + 500
  = 2500

두 경우 모두 조인에 사용되는 비용은 500으로 같지만 버퍼에 할당된 페이지의 수가 많을수록 정렬에 드는 비용이 줄어들어 전체 조인비용이 줄어든다.

앞의 Nested-loop Join과는 다르게 Merge join은 s.id = t.id 꼴의 equi-join만 지원한다는 단점이 있다. 하지만 대부분의 조인 연산이 equi join에 의해 이루어지기 때문에 큰 단점은 아니다.

Hash Join

Hash Join은 equi-join연산에 대해 버퍼에 할당된 페이지의 수가 많아 비교적 넉넉한 메모리 공간을 사용할 수 있을 때 쓰는 조인 방법으로, 전체 레코드를 해시함수를 통해 파티션으로 나누고, 각 파티션에 대해 조인 연산을 수행한다.

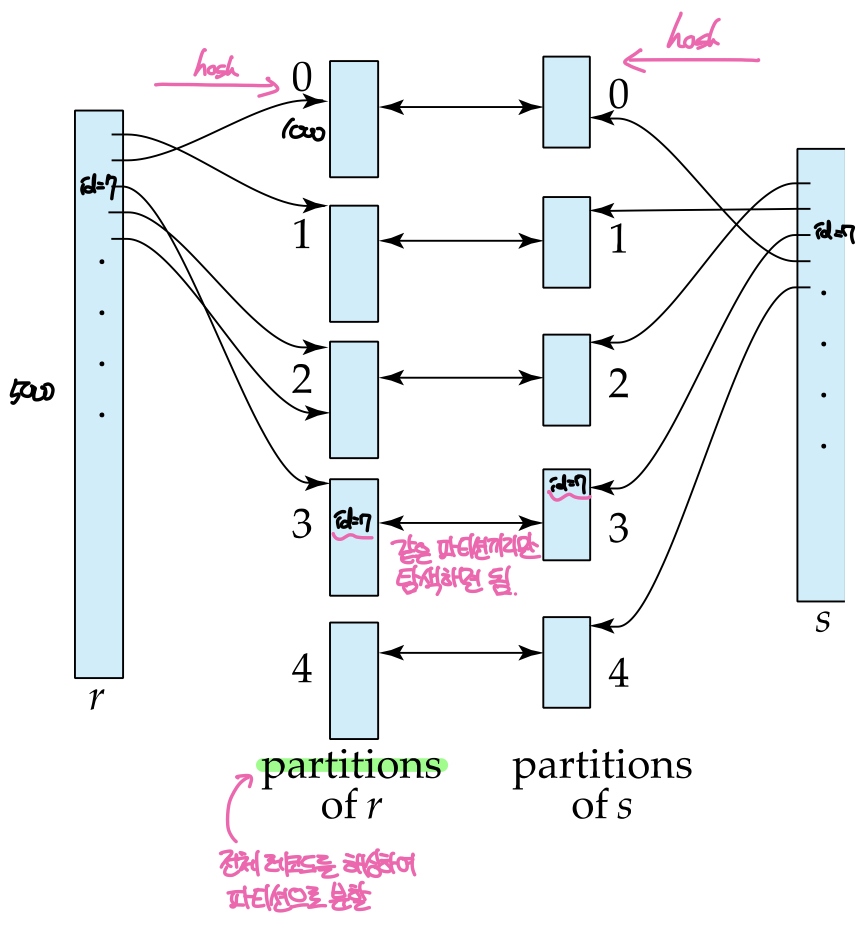
그림과 같이 양쪽 테이블을 같은 해시함수를 사용하여 파티션으로 분할하면 조인 키값이 같은 레코드는 같은 번호의 파티션으로 매핑되므로 같은 파티션끼리만 비교하면 매칭되는 쌍을 찾을 수 있다.

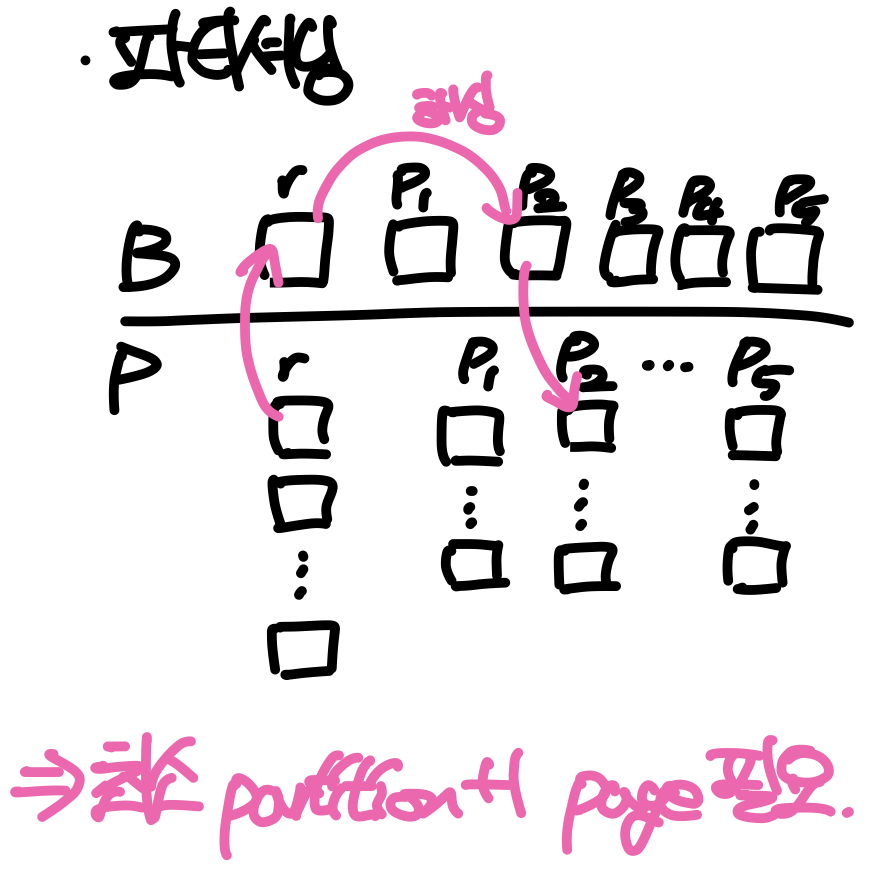
파티셔닝을 위해서는 버퍼에 최소 파티션 수 + 1개 만큼의 페이지가 필요하다. 버퍼의 1페이지는 원본 테이블의 블록을 올리는 데 사용되고, 나머지 페이지들은 각 파티션에 저장될 레코드를 보관한다. 전체 파티셔닝 과정은 다음과 같다. 먼저 원본 테이블에서 1블록을 버퍼로 올린 뒤 각 레코드를 해싱하여 각 파티션으로 분배하고 다음 블록을 올린다. 만약 파티션 페이지가 가득 찼다면 해당 페이지를 디스크에 쓰고 페이지를 비운다. 만약 파티셔닝시 버퍼에 페이지가 부족하다면 여러 단계에 거쳐 파티셔닝을 수행 할 수도 있지만, 기본적으로 해시조인은 버퍼에 할당된 페이지의 수가 넉넉할 때 사용하는 방법이므로 여기서는 고려하지 않는다.

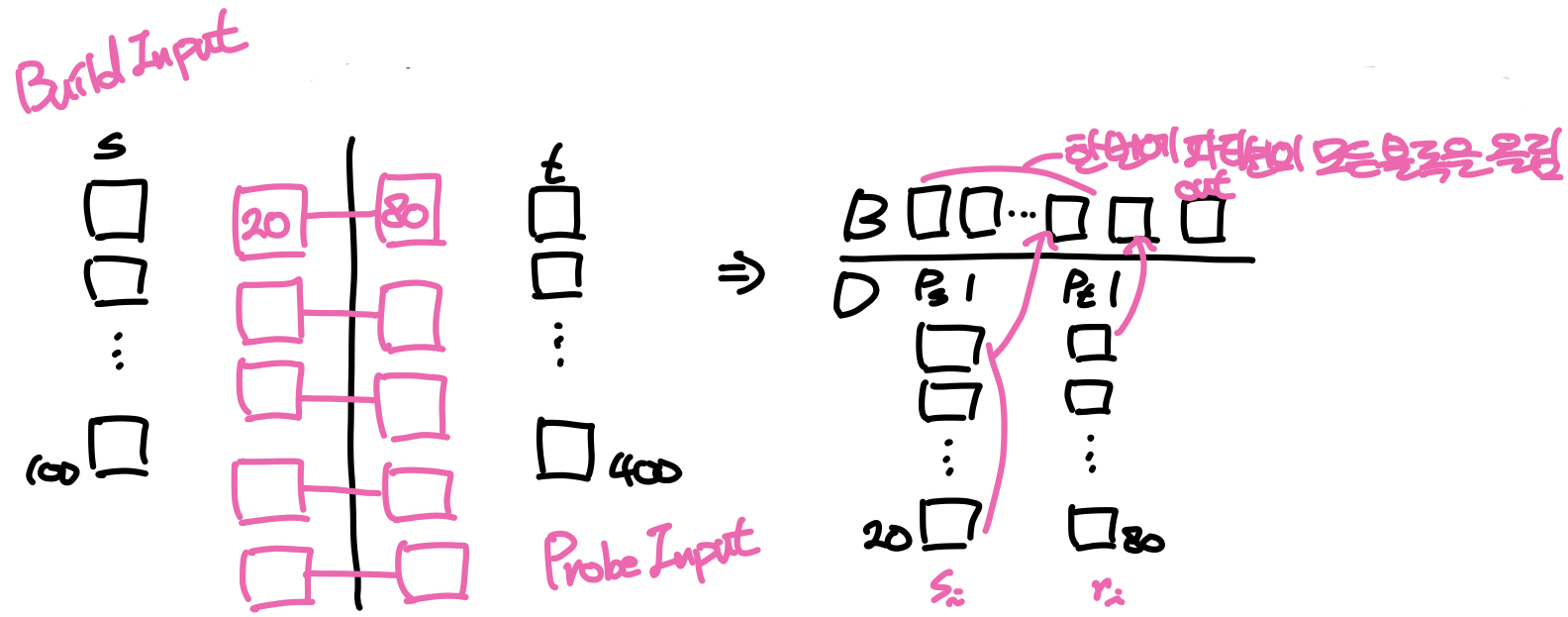
파티셔닝이 완료되었으면 본격적인 조인 연산을 위해 버퍼에 한 파티션의 블록 수 + 2만큼의 페이지를 할당하고 한쪽 파티션의 모든 블록을 버퍼로 올린다. 버퍼의 나머지 두 블록은 각각 반대편 파티션 블록을 올리고 조인 결과를 기록하기 위한 용도로 사용된다. 이때 파티션 전체가 올라오는 쪽의 테이블을 build input이라 하고, 반대쪽을 probe input이라 한다. 즉, build input의 한 파티션 전체를 버퍼에 올리고 probe input의 파티션을 한블록씩 버퍼에 올리면서 비교연산을 수행하고 결과값을 output page에 기록하는 방식으로 조인 연산이 이루어진다. 따라서 버퍼에 필요한 페이지수는 엄밀히 따지면 Build input의 한 파티션에 속한 블록 수 + 2로 볼 수 있다.

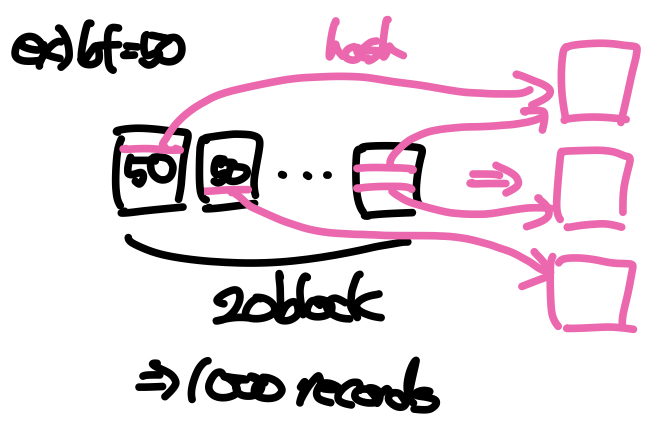
조인과정에서 probe input의 블록이 버퍼에 올라오면 각 레코드마다 미리 버퍼에 올라와 있는 build input의 파티션에서 조건에 맞는 레코드를 찾아야 한다. 이때 모든 페이지를 탐색하면 전체 조인연산의 비용이 증가하기 때문에 버퍼에 올라온 build input파티션에 대해 in-memory hash index를 만들어 레코드를 탐색하는 속도를 높인다. 이때 인 메모리 해시인덱스를 구성하기 위해 사용하는 해시함수는 파티셔닝에 사용되는 것과는 별개의 것이다.

해시 조인을 요약하자면 모든 블록을 읽어서 파티션을 나눈 뒤 디스크에 쓰고 다시 모든 파티션을 읽어서 조인하는 알고리즘이다. 따라서 각 과정에서 대략적으로는 전체 블록 수만큼의 I/O가 발생하기 때문에, 해시 조인의 비용식은 다음과 같이 작성할 수 있다.

Hash Join : Cost = 3(br + bs) (파티셔닝(2 * I/O) + 조인(1 * I/O))

이때 해싱으로 인해 원본 테이블의 블록 수보다 추가되는 블록(fragmentation)이 생길 수 있는데, 식에서는 무시하고 계산하였다. 또한 버퍼에는 충분한 양의 페이지가 할당되었다고 가정하였다.

student와 takes를 해시조인 알고리즘을 통해 조인하면 비용은 다음과 같이 계산할 수 있다.

• Cost = 3(100 + 400) = 1500
  • build input : students, # of partitions = 5, # of blocks in each partition = 20
  • probe input : takes, # of partitions = 5, # of blocks in each partition = 80
  • # of buffer pages = 22

만약 위의 예시에서 파티션의 수를 10개로 설정하였다면, build input의 파티션당 블록수가 10개로 줄어들게 되어 버퍼에 최소 12페이지만 할당되어도 해시조인 연산을 수행할 수 있다.