Query Processing
사용자는 데이터베이스를 사용하기 위해 DBMS에 Query를 전달하고, DBMS는 이를 받아 해석하여 사용자가 주문한 작업을 수행하는데, 이 과정을 Query Processing(질의 처리)이라고 한다. 대부분의 DBMS는 SQL쿼리를 사용하는데, SQL을 사용하면 사용자의 입장에서 DBMS에게 자신이 원하는 데이터만 알려주고 데이터를 조회하거나 처리하는 방법은 DBMS가 알아서 선택한다. 따라서 SQL을 선언적 질의어라고도 한다.
DBMS의 질의 처리는 크게 3단계로 구성된다.
- Parsing, Translation : 쿼리문을 파싱하고 관계대수 식으로 변환하는 작업
- Optimization : 질의 최적화
- Evaluation : 최적화된 관계대수식을 보고 작업을 수행하여 결과를 도출하는 작업
좀 더 구체적인 과정은 아래 그림과 같다.
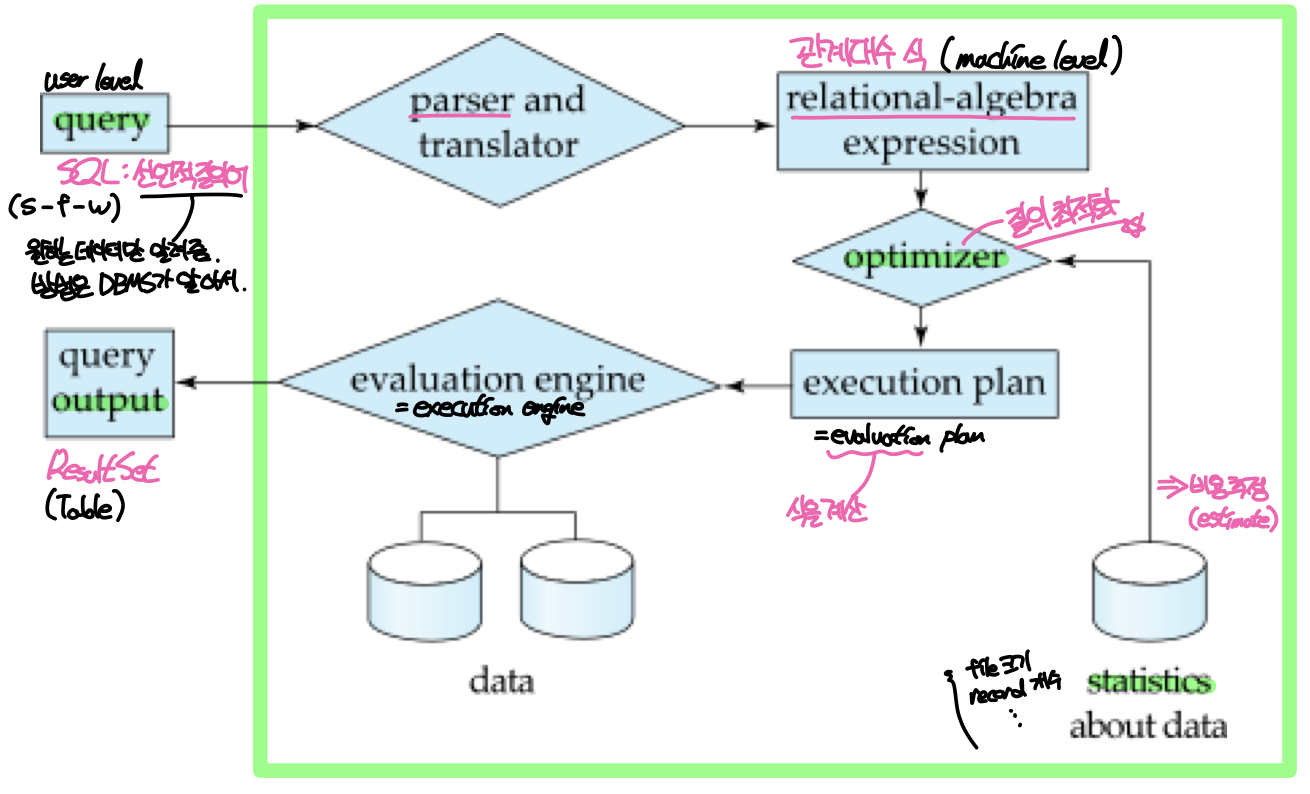
먼저 사용자는 DBMS에게 쿼리문을 전송한다. DBMS는 이 쿼리를 받아 파싱하고 해석하여 관계대수 식으로 변환한다. 그런데 같은 쿼리문이라도 관계대수 식으로 변환하는 과정에서 여러 경우의 수가 나올 수 있기 때문에 DBMS는 데이터에 대한 통계자료(파일의 크기, 레코드의 수 등)들을 통해 각각의 질의에 대한 비용을 추정(estimate)하여 가장 적은 비용으로 원하는 데이터를 도출할 수 있는 질의를 선택한다. 그 후 최적화된 식을 계산(evaluate)하고 실행하여 디스크에서 데이터를 찾고, output으로 사용자에게 ResultSet을 반환한다.
관계대수
관계대수란 질의를 어떻게 처리할 것인지를 명시하는 언어로 DBMS의 질의 처리과정에서 사용되는 중간 처리 언어이다. 관계대수는 릴레이션을 대상으로 연산을 수행하며, 기존 릴레이션들로부터 새로운 릴레이션을 만들어낸다는 특징이 있다.
관계 연산자는 관계대수 식을 만드는 연산자로 대표적으로 아래와 같은 종류가 있다.
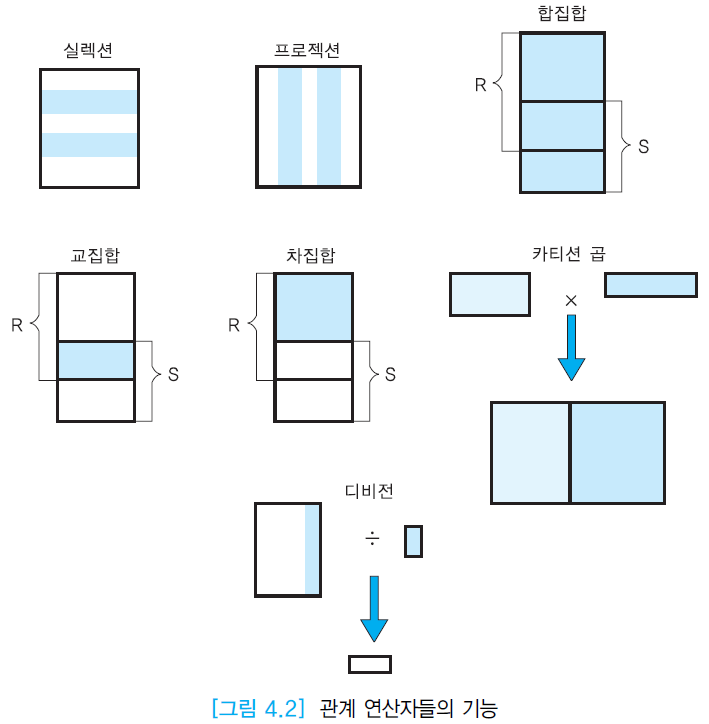
- Selection(σ) : 한 릴레이션(테이블)에서 조건(Predicate)을 만족하는 튜플들을 선택(row). σ<predicate>(R)
- Projection(π) : 한 릴레이션(테이블)에서 attribute들을 선택(column). π<attributes>(R)
- Join(⋈) : 두 릴레이션(테이블)에서 공통 속성을 중심으로 연관된 튜플을 결합하여 새로운 릴레이션을 생성. R⋈R.ai θ S.bjS
- R, S는 릴레이션 이름, R.ai, S.bj는 공통속성, θ는 조인조건이다.
- Division(÷) : 두 릴레이션 R, S에서 S가 R의 부분집합일때 S의 모든 속성을 가진 R의 튜플. R ÷ S
Query Optimization
관계대수 식은 동일한 결과를 내는 여러개의 식으로 표현될 수 있다. 예를 들어 select salary from instructor where salary < 75,000 이라는 쿼리문이 주어졌을 때 이를 관계대수 식으로 나타내면 σsalary<75000(πsalary(instructor)) 라고 식을 세울 수 있지만 selection연산을 먼저 수행해서 πsalary(σsalary<75000(instructor)) 으로도 나타낼 수 있다. 전자의 식은 먼저 salary column을 project하고 그 중에서 값이 75,000보다 작은 레코드를 select하는 방법이고, 후자는 먼저 salary값이 75,000보다 작은 레코드를 selec한 뒤 salary column을 project하는 방식이다. 최종적으로는 두 식 모두 같은 결과를 도출한다.
또한 각각의 관계대수 연산자는 다양한 알고리즘으로 구현될 수 있다. 예를 들면 위의 쿼리문에 중복을 제거하는 distinct 키워드가 추가되었다고 하면 projection과정에서 해싱 알고리즘을 사용할 수도 있고, 정렬을 통해 중복을 제거할 수도 있다. 따라서 같은 관계대수 식이라도 각 연산자가 사용하는 알고리즘에 따라 다른 방식으로 동작할 수 있기 때문에 각 연산자에 어노테이션으로 사용하는 알고리즘의 종류를 표시하여 구분하고, 이를 evaluation plan이라고 한다.
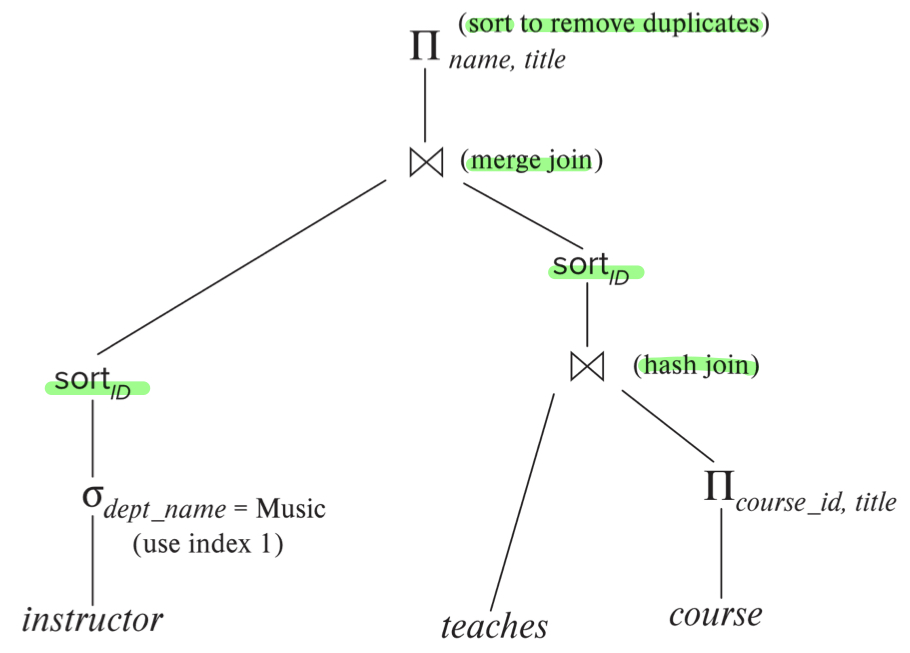
evaluation plan에는 각 연산자에 어떤 알고리즘이 사용되었는지와 전체 연산자가 어떤 순서로 실행되는지에 대한 정보가 담겨있다. 하나의 쿼리는 여러개의 동등한 evaluation plan으로 나타낼 수 있는데, 그 중 가장 비용이 적은 것을 선택하는 것이 바로 질의 최적화이다. 이때 각 plan의 비용은 실행하기 전까지는 알 수 없기 때문에 데이터베이스에 저장된 통계자료(각 릴레이션의 튜플 수, 튜플의 크기 등)를 활용하여 추정(estinated)한 것을 사용한다.
Query cost
쿼리 비용은 응답시간(response time)과 자원 소비량(resource comsumption)을 바탕으로 측정된다. 응답시간은 사용자가 쿼리를 전송한 순간부터 결과를 받기까지 걸리는 시간으로 응답시간이 높을수록 비용이 크다고 볼 수 있다. 하지만 응답시간은 추정하기 어렵기 때문에 비용을 추정할 때 잘 사용하지 않는다. 자원소비량에는 I/O횟수, CPU time, 통신시간등이 포함되는데 그중 I/O에 사용되는 시간이 가장 크기 때문에 다른 요소들은 무시하고 I/O횟수만 고려한다.
비용추정을 위해 I/O횟수를 계산할 때 주의할 점은 plan의 최종 결과를 디스크에 쓰는 작업은 포함하지 않는다. 한정된 버퍼공간으로 인해 plan을 실행할 때에는 중간결과를 디스크에 쓰고 다음 작업을 이어가야 한다. 따라서 엄밀히 따진다면 최종결과를 쓰는 작업 역시 비용에 들어가야 하지만, 비교하는 모든 plan의 최종 결과는 같기 때문에 이를 디스크에 쓰는 작업은 모든 plan에서 동일하므로 비용에 포함하는 것은 무의미하다.
또한 각 plan을 수행할 때 원하는 블록이 이미 버퍼에 올라와있거나 할당된 버퍼의 크기가 다르다면 성능에 영향을 줄 수 있다. 하지만 이런 경우들은 예측하기에는 어려우므로 비용을 추정할 때에는 Worst case만 고려하여 모든 데이터는 디스크에 있고 제공되는 버퍼는 최소한의 크기만 주어진다고 가정해야 한다.
Selection 알고리즘
Selection연산(σ) 테이블에서 조건에 맞는 레코드를 찾는 연산으로, 파일을 전체를 탐색하는 방법과 인덱스를 사용하여 탐색하는 방법이 있다.
Equality
σid = 1 과 같은 specific selection연산을 처리하는 방법은 다음과 같다.
Linear File Scan
테이블의 모든 레코드를 순차적으로 탐색하여 원하는 값을 찾는 방법으로 파일의 모든 디스크 블록을 하나씩 메모리 버퍼로 올리면서 조건에 맞는 값을 찾는다. 이때 버퍼에는 디스크 블록을 올릴 공간과 연산 결과를 저장할 공간이 필요하므로 최소 2페이지가 할당된다. 이때 비용 Cost는 테이블의 레코드가 포함된 블록 개수 b와 같다.
Linear Search : Cost = b (테이블의 블록 개수)
만약 selection의 조건이 PK에 대한 것이라면 해당 레코드를 찾은 뒤에는 탐색을 중지하기 때문에 평균적인 비용은 b/2가 된다.
Linear Search Equality on Key : (Average case) Cost = b/2 (테이블의 블록 개수 / 2 : best case = 1, worst case = b)
Linear Search 알고리즘은 다른 알고리즘 보다 느릴 수 있지만 selection의 조건, 레코드의 순서 및 인덱스의 유무에 관계없이 항상 적용할 수 있는 방법이다.
Index Scan
인덱스를 사용한 탐색 알고리즘으로, selection의 조건은 반드시 인덱스의 search key에 대한 것이어야 한다.
Clustering index, Equality in key
집중 인덱스를 사용하고 selection의 조건이 키 컬럼에 대한 equality일때, B+트리를 탐색하여 레코드의 위치를 찾은 뒤 레코드가 포함된 블록을 버퍼로 올린다. 이때 비용은 B+트리의 각 노드 블록을 버퍼에 올리는 작업과 레코드가 포함된 블록을 올리는 작업의 합으로 계산한다.
Clustering index, Equality in key : Cost = h + 1 (B+트리의 높이 + 레코드가 포함된 블록 I/O)
Clustering index, Equality in non-key
집중 인덱스를 사용하지만 키가 아닌 컬럼에 대한 equality조건인 경우로, 복수개의 레코드가 결과로 나올 수 있다. 이 경우 B+트리를 탐색하여 조건에 맞는 레코드의 시작위치를 찾은 뒤 레코드가 포함된 모든 블록을 버퍼로 가져온다. 이 때 집중 인덱스를 사용하므로 조건에 맞는 레코드들은 연속된 블록에 모여있다.
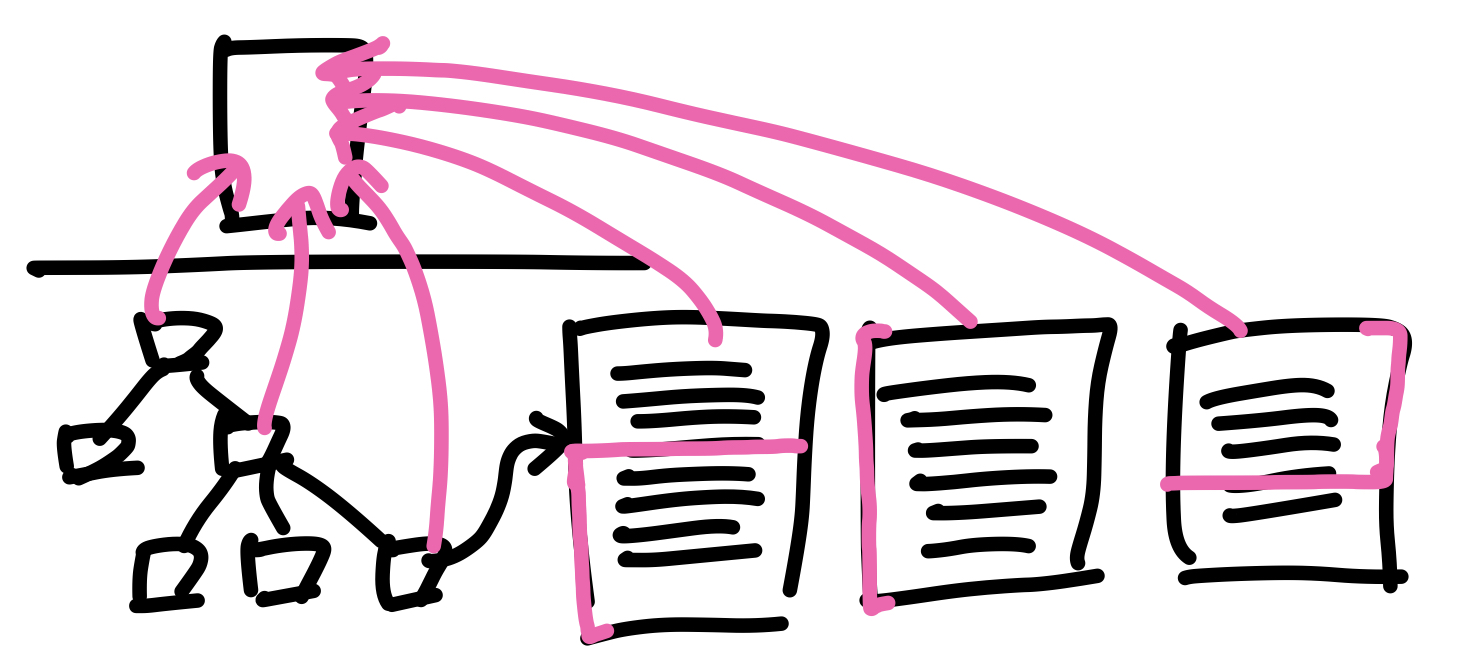
Clustering index, Equality in non-key : Cost = h + b (B+트리의 높이 + 레코드가 포함된 블록 개수)
Secondary index, Equality
비 집중 인덱스를 사용하는 경우 테이블에 저장된 레코드의 순서는 인덱스가 정렬된 순서와 다르기 때문에 인덱스의 leaf node에는 각 레코드로의 포인터가 존재한다. 만약 search key가 후보키라면(레코드가 유일하다면) B+트리를 탐색한 뒤 해당 레코드 블록을 가져오면 되고, 만약 후보키가 아니라면(유일하지 않다면) 여러개의 레코드가 존재할 수 있기 때문에 B+트리를 탐색하고 leaf node가 가리키는 모든 포인터의 블록을 가져온다. 최악의 경우 모든 레코드가 서로 다른 블록에 존재할 수 있는데, 이 경우에는 트리의 높이 + 레코드의 수 만큼의 I/O작업이 필요하다. 따라서 비 집중 인덱스의 경우 특정 상황에서는 인덱스를 사용하지 않는 것이 더 빠를 수 있다.
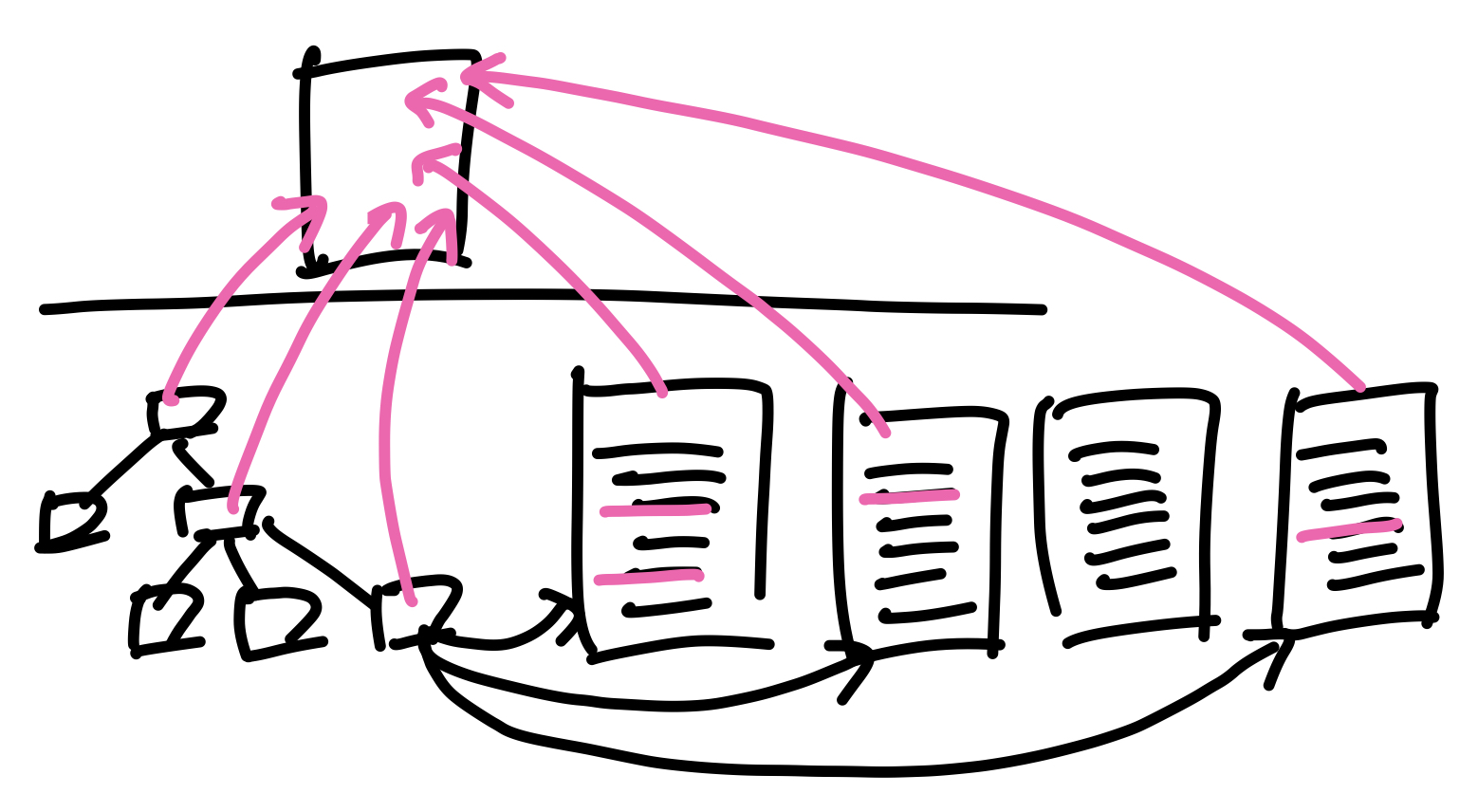
Secondary index, Equality in key : Cost = h + 1 (B+트리의 높이 + 레코드가 포함된 블록 I/O)
Secondary index, Equality in non-key : Cost = h + n (B+트리의 높이 + 레코드가 포함된 블록 개수, n >= b)
Comparisons
σid >= 1, σid <= 10 과 같은 range selection연산을 처리하는 방법은 다음과 같다.
Linear File Scan
Equality조건을 처리하는 경우와 같이 모든 파일을 순차적으로 탐색하므로 비용은 테이블의 모든 블록 수와 같다.
Linear File Scan : Cost = b (테이블의 블록 개수)
Index Scan
Clustering index, Comparison
>= 조건의 경우, 먼저 조건을 만족하는 첫번째 레코드를 인덱스에서 찾는다. 집중 인덱스를 사용하기 때문에 레코드가 정렬되어 있으므로 찾은 레코드의 뒤에 있는 레코드들은 모두 조건을 만족하므로 테이블의 마지막까지 탐색하며 블록을 버퍼로 가져온다.
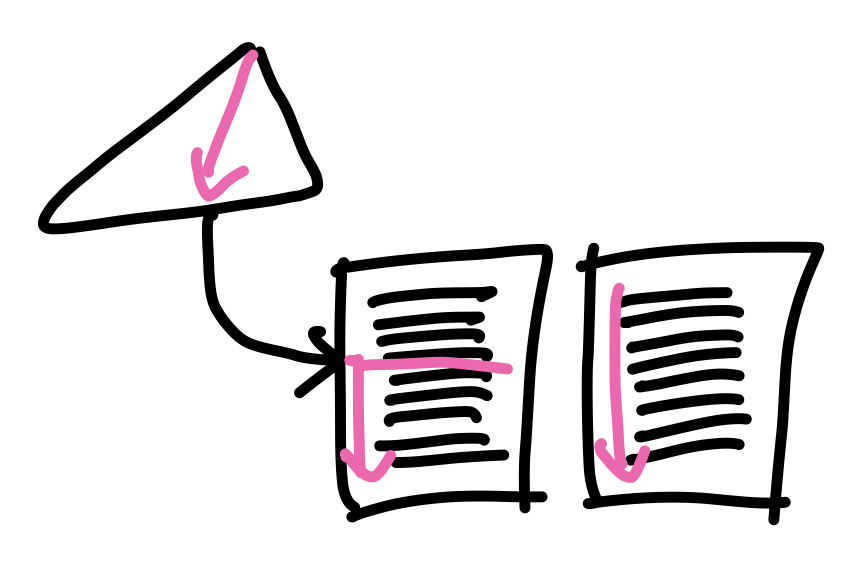
<= 조건의 경우, 집중 인덱스를 사용하기 때문에 레코드가 정렬되어 있으므로 처음부터 조건을 만족하지 않는 레코드가 나올 때까지 탐색하면서 블록을 가져온다. 이 경우는 인덱스를 사용하지 않고 단순히 파일을 스캔하는 것 만으로도 가능하기 때문에 인덱스를 사용하는 것이 오히려 더 비용이 크다.
Clustering index, Comparison : Cost = h + b (B+트리의 높이 + 레코드가 포함된 블록 개수)
Secondary index, Comparison
비 집중 인덱스의 경우 인덱스의 정렬 순서와 레코드의 정렬 순서가 같지 않기 때문에 각 leaf node가 가리키는 포인터를 통해 레코드에 접근해야 한다.
>= 조건의 경우, 인덱스에서 조건을 만족하는 엔트리를 찾은 뒤, leaf node를 따라 인덱스의 마지막까지 이동하면서 각 노드가 가리키는 블록을 가져온다. 집중 인덱스와 달리 인접한 노드의 레코드가 서로 다른 블록에 있을 수 있기 때문에 조건에 맞는 레코드를 일일히 탐색해야 한다.
<= 조건의 경우도 위와 비슷하게 leaf node를 따라 이동하면서 각 노드가 가리키는 블록을 버퍼로 가져오는데, 이 때 인덱스를 탐색하는 범위는 인덱스의 첫번째 leaf node부터 조건을 만족하지 않는 노드가 나올 때 까지이다. 최악의 경우 모든 레코드가 서로 다른 블록에 있을 수 있는데, 이 경우 파일 스캔이 더 효율적일 수 있다.
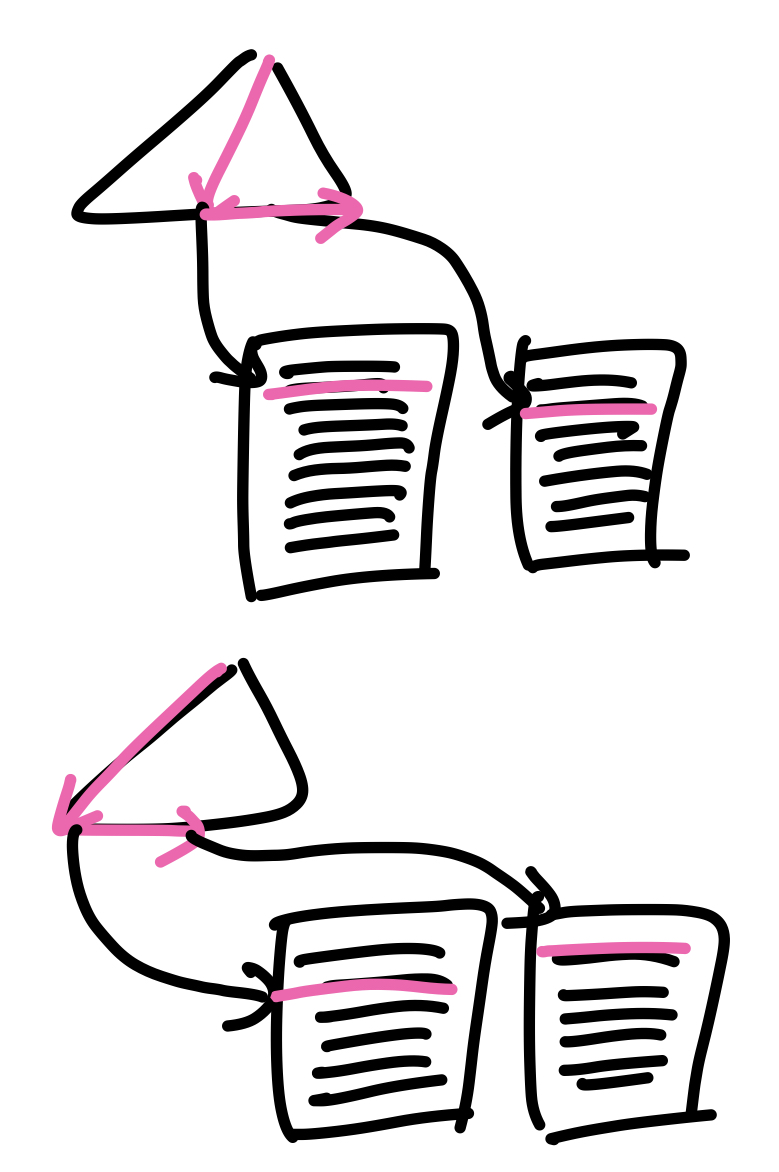
Secondary index, Comparison : Cost = h + n (B+트리의 높이 + 레코드가 포함된 블록 개수, n >= b)
Sorting 알고리즘
External Sorting
릴레이션의 모든 데이터가 메모리에 올라올 수 있는 경우 퀵정렬 등과 같은 Internal sorting알고리즘을 사용하여 정렬할 수 있다. 하지만 일반적으로 데이터베이스 환경에서 모든 데이터가 메모리에 올라오는 경우는 극히 드물다. 따라서 데이터가 디스크에 있는 상태로 정렬하는 알고리즘이 필요한데, 이때 사용하는 것이 External sorting알고리즘이다.
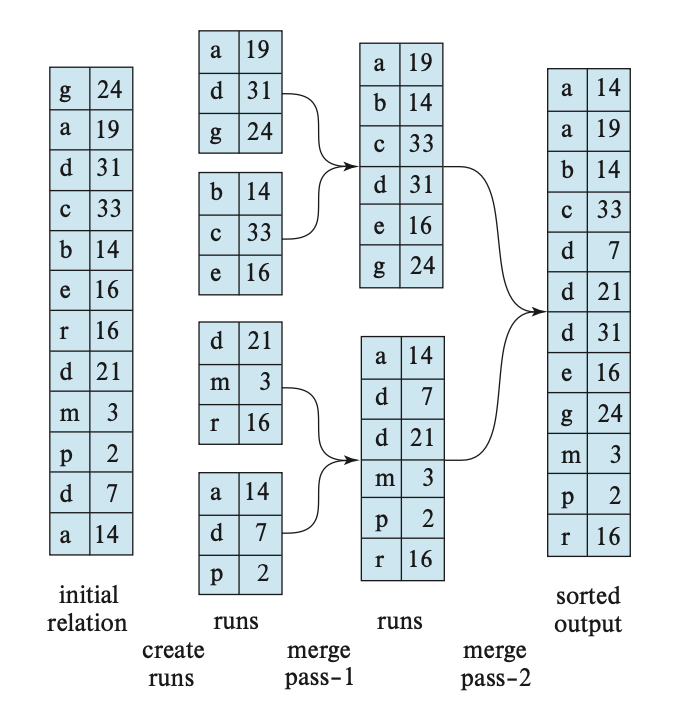
External sorting의 기본 동작방식은 "데이터를 메모리에 올릴 수 있는 단위로 나눈 뒤 각각에 대해 Internal sorting후 병합하여 디스크에 기록하는 것"이다. 여기에서 전체 데이터를 메모리에 올릴 수 있는 단위로 나눈 것을 Run이라 한다. External sorting은 크게 초기 런 생성 -> 정렬 -> 병합 3단계를 반복하여 최종적으로 1개의 런이 남을 때까지 수행된다.
초기 런 생성 및 정렬
정렬을 위한 런을 만들기 위해 디스크에 있는 릴레이션에서 버퍼에 M개의 블록을 올린 뒤, 메모리에 올라온 블록들을 정렬한다. 이때 버퍼에는 결과를 기록하기 위한 1개의 페이지(output buffer page)가 추가로 필요하다. 위의 예시에서는 3개의 레코드 블록[(g,24), (a,19), (d,31)]을 버퍼로 올린 뒤 정렬하여 초기 런을 만들고 디스크에 기록하였다. 이 과정을 테이블의 모든 데이터에 대해 반복하여 최종적으로 초기 런의 개수 N을 얻는다.
런 병합
초기 런을 만든 이후, 각 런에서 한 블록씩 버퍼로 올린 뒤 버퍼에 올라온 블록들을 정렬하여 병합한다.
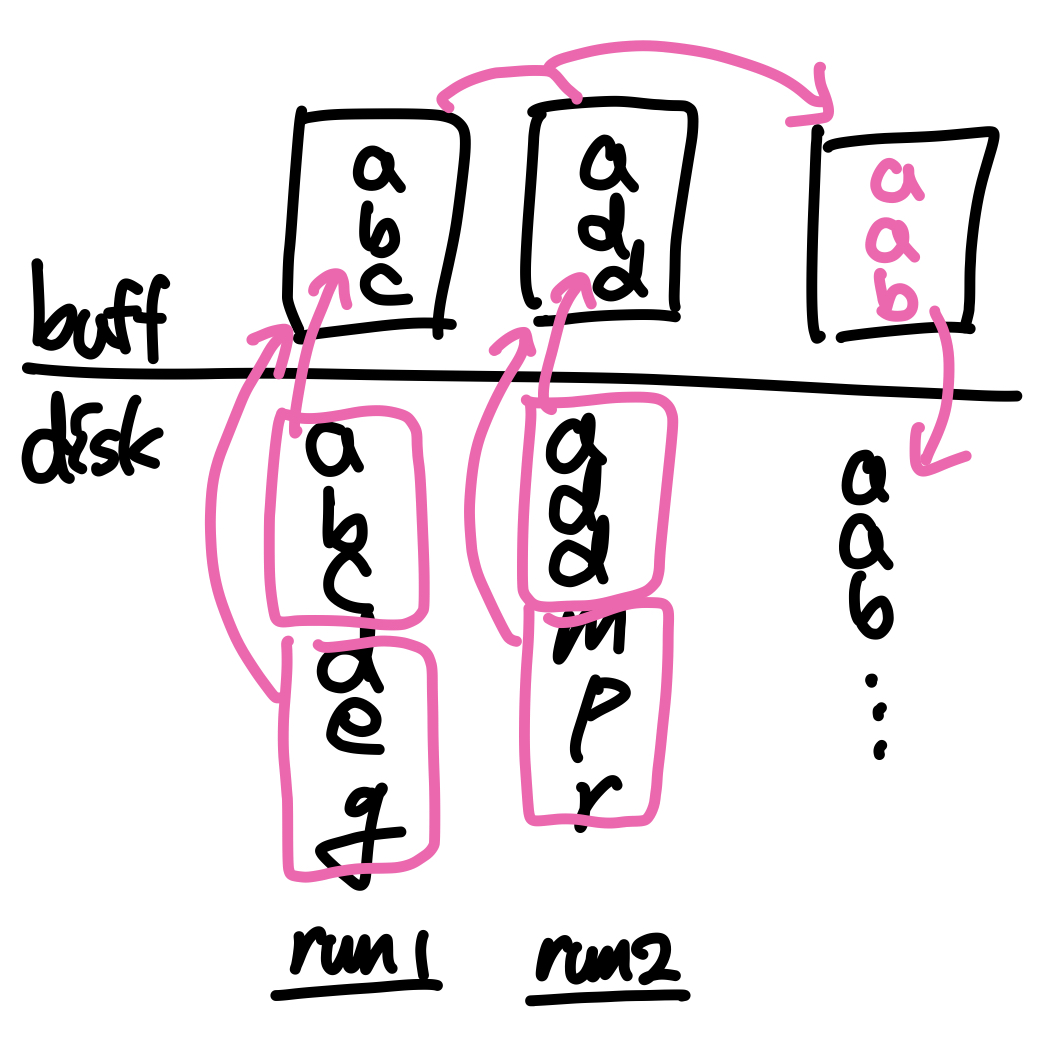
런을 병합하는 과정은 다음과 같다.
- 각 블록에 포인터를 하나씩 두고 값을 비교해가며 가장 작은 값을 output buffer page에 복사하고 해당 블록의 포인터를 하나 증가시킨다.
- 이후 output buffer page가 가득차게 되면 결과를 디스크에 저장하고 페이지를 비운 뒤 병합을 계속 진행한다.
- 만약 어떤 블록의 모든 레코드를 탐색했다면 해당 런의 다음 블록을 로드한 뒤 병합을 이어나간다.
이후 모든 런을 병합했다면 다음 단계의 런을 로드하여 같은 과정을 반복한다. 이때 버퍼에 할당된 페이지의 수 M과 디스크에 있는 런의 개수 N에 따라 병합 방법이 달라진다.
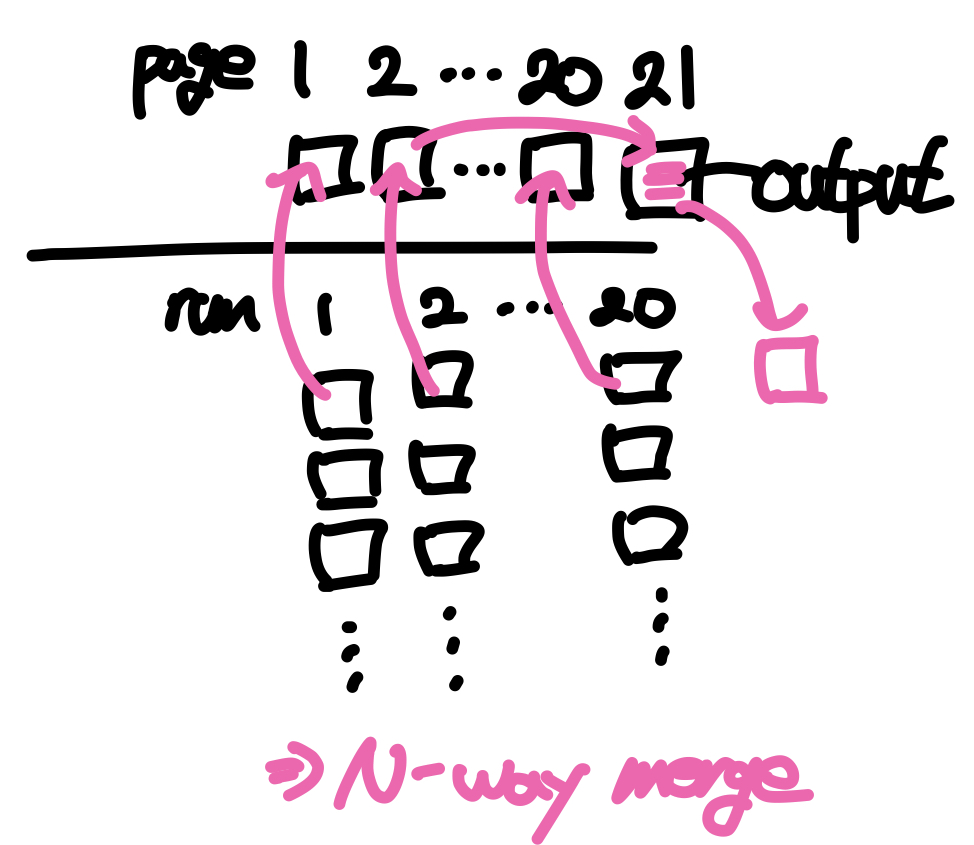
버퍼의 페이지 수가 런의 수보다 많은 경우(M > N) N-way merge를 수행하게 되는데, 모든 런에서 한 블록씩 버퍼에 올리고 결과를 output beffer page로 복사하여 디스크에 저장한다. 이 경우에는 병합의 결과로 1개의 런이 나오기 때문에 정렬이 끝이 난다.
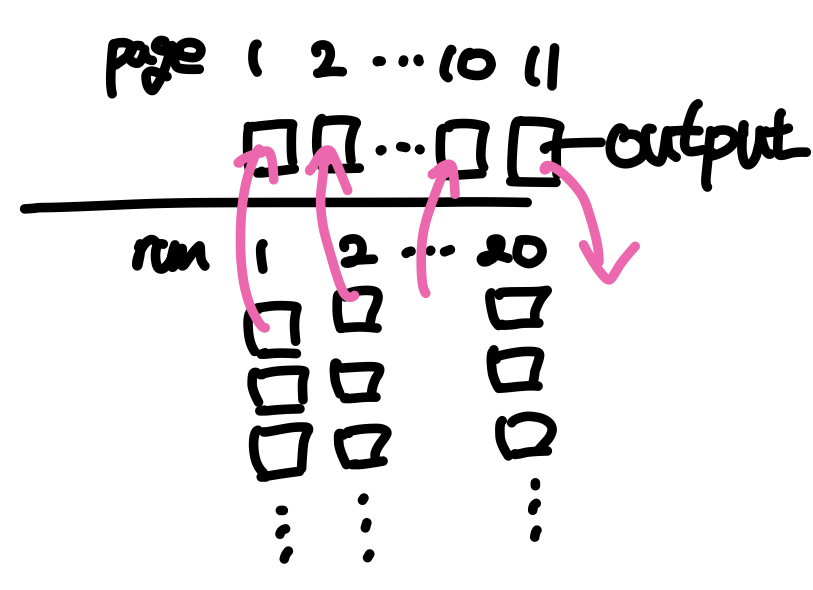
반면, 버퍼의 페이지 수가 런의 수보다 작거나 같은 경우(M <= N) (M-1)-way merge를 수행한다. 이 경우, 버퍼의 전체 페이지 중에서 하나는 output beffer page로 사용하고 나머지 페이지의 개수(M-1)만큼의 런에서 블록을 하나씩 올려 병합을 수행하게 된다. 이때 M-1은 N보다 작기 때문에 병합이 한번에 끝나지 않아 여러개의 런이 만들어지게 된다. 따라서 전체 데이터를 정렬할 때까지 여러번의 병합과정을 거치게 되는데, 각각의 병합과정을 merge-pass라고 한다.
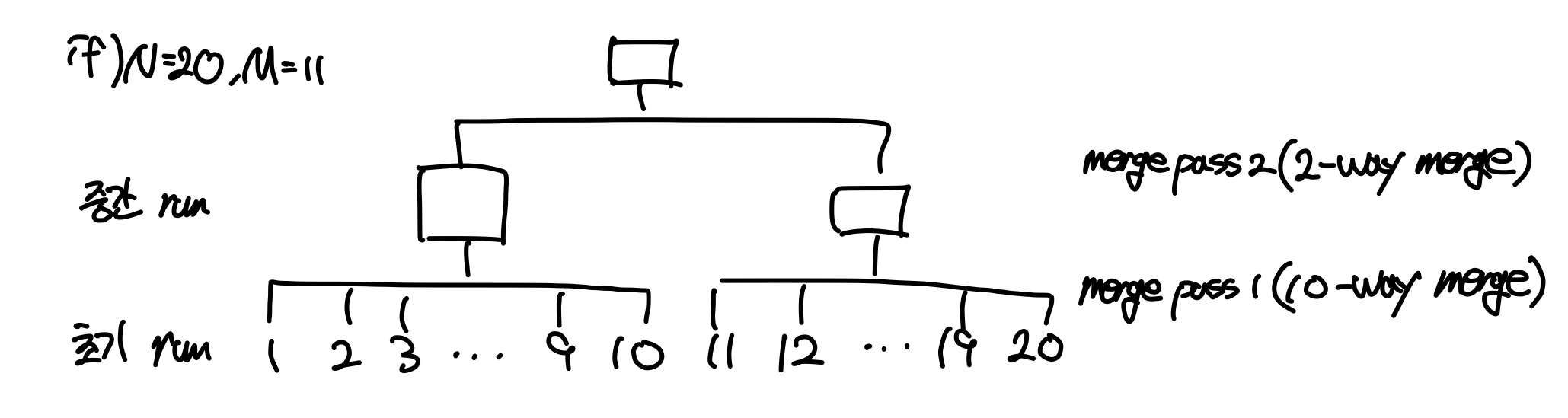
위의 예시는 초기 런이 20개이고 버퍼에 할당된 페이지가 11개인 상황에서 External sorting을 수행하는 과정으로, merge-pass 1에서 한번에 10개의 런을 병합하여 총 2개의 중간 런을 만들고, 이후 merge-pass 2에서 두 런을 병합하여 최종 결과를 도출한다.
Cost
External Sorting의 비용은 다음과 같은 식으로 계산할 수 있다.
External Sorting(중간 연산) : Cost = 2b(ceil(logM-1(b/M))) + 2b = 2b(ceil(logM-1(b/M)) + 1)
External Sorting(최종 연산) : Cost = 2b(ceil(logM-1(b/M)) + 1) - b = b(2 * ceil(logM-1(b/M)) + 1)
b는 릴레이션에 있는 전체 블록의 수이고, M은 버퍼에 할당된 페이지의 수이다.
식을 해석하자면, 먼저 b/M은 릴레이션의 전체 블록 수를 버퍼 페이지 수로 나눈 것으로 초기 런의 수를 의미한다. 또한 각 merge-pass당 M-1개의 런이 병합되므로 초기 런의 수를 밑이 M-1인 로그를 통해 전체 Merge-pass의 횟수를 구한다. 그리고 여기에 곱해지는 2b는 각 merge-pass당 I/O의 횟수로 1번의 merge-pass과정에서는 전체 릴레이션의 모든 블록들이 메모리로 read되고 병합된 결과가 디스크로 write되어야 하므로 merge-pass당 2b만큼의 I/O가 발생하게 된다.
중간 연산 식에서 마지막에 더해지는 2b는 초기 런을 만들기 위한 I/O의 횟수로 초기 런을 만들 때 전체 블록을 메모리로 올리고 결과로 만들어진 런을 디스크에 쓰는 작업이 필요하다. 이때, 최종 연산의 비용 식에서는 b를 한번 빼주는데, 이는 최종 결과를 디스크에 wtire하는 비용으로 중간 결과에서와 달리 최종결과를 디스크에 쓰는 작업은 비용에 포함하지 않기 때문에 b만큼의 I/O횟수를 빼서 식을 완성한다.
전체 식의 의미를 정리하면 아래와 같다.
- b/M : 초기 런의 수
- logM-1(b/M) : Merge-pass의 횟수
- *2b : 각 merge-pass당 I/O의 횟수
- +2b : 초기 런을 만들기 위한 I/O의 횟수
- (최종 연산) -b : 최종 결과를 디스크에 wtire하는 비용
