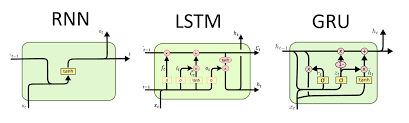
RNN(Recurrent Neural Network) 순환 신경
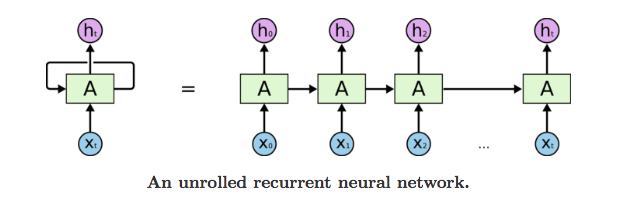
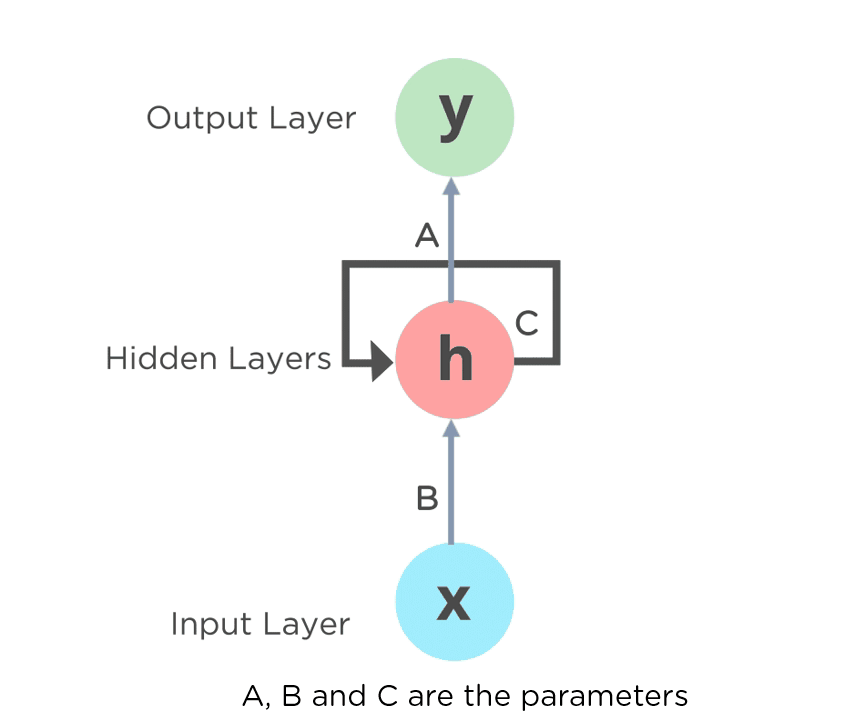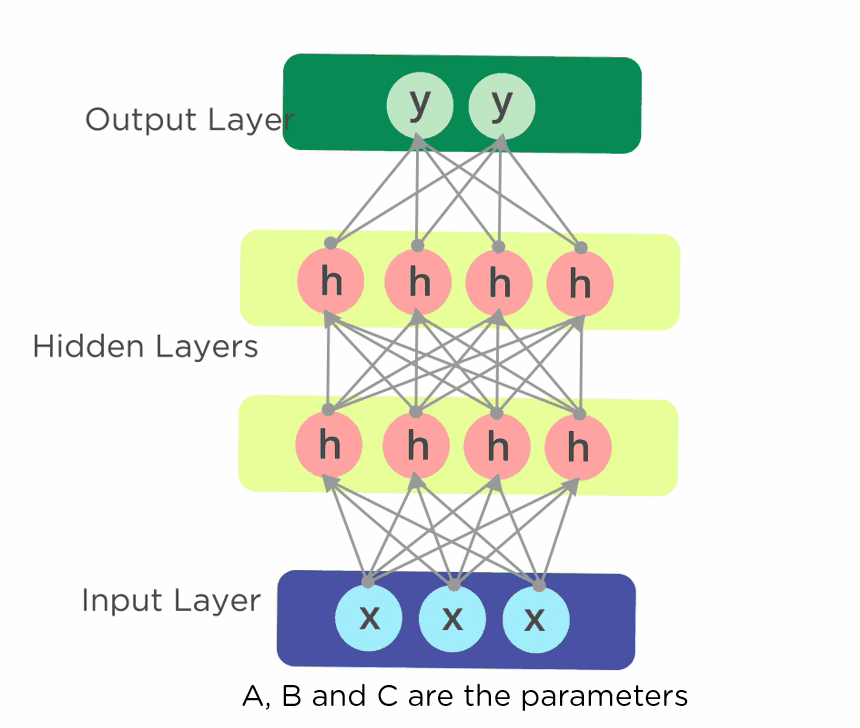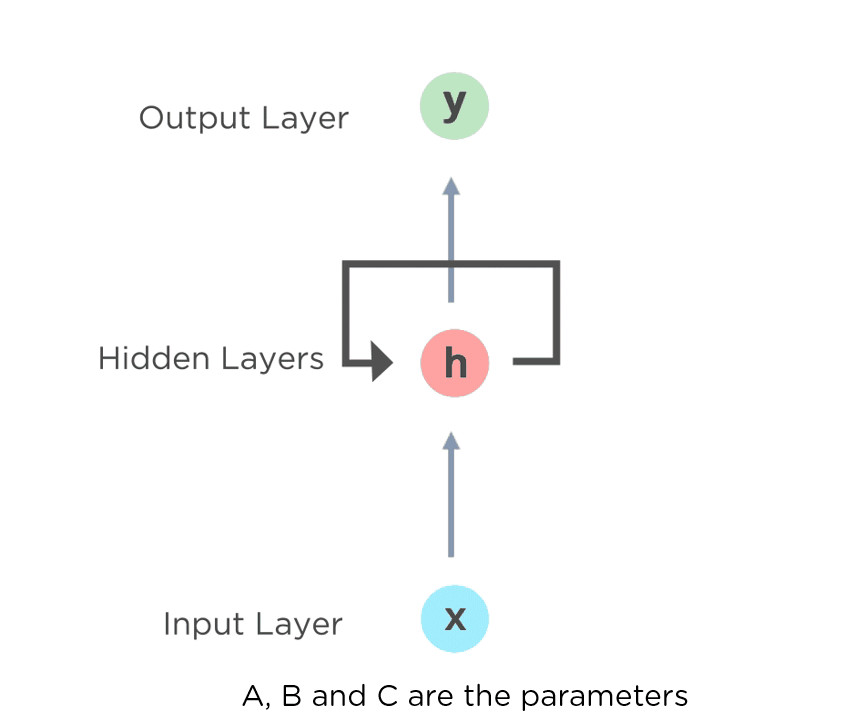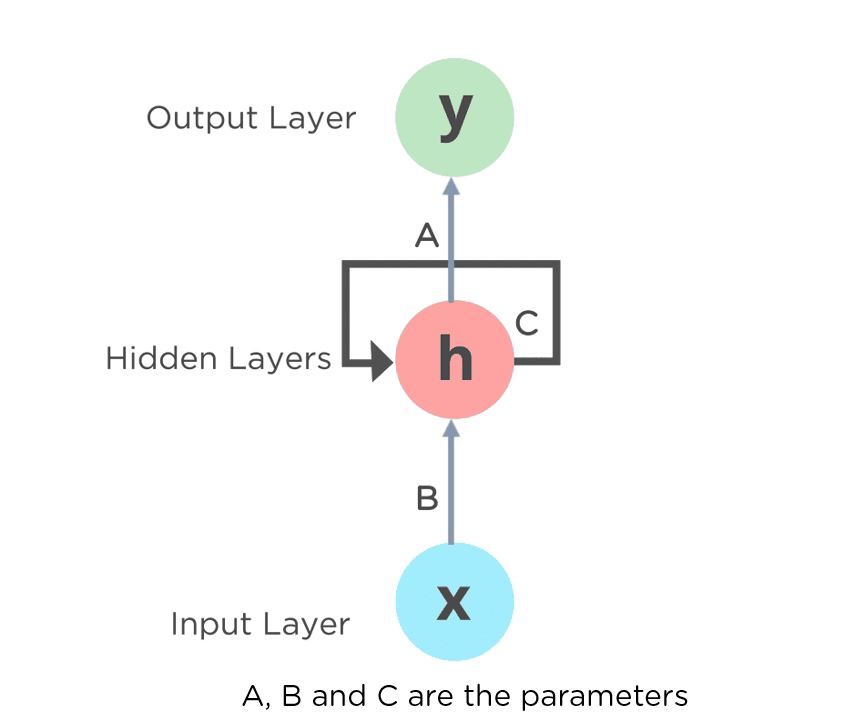
위의 오른쪽 그림에서 펼처진 순환구조는 평소에 보던 신경망과 대조해서 보면 다른 Layer의 노드처럼 보일 수 있지만 실제로 같은 계층이다.
여기서 ht는 이전 출력(ht-1)을 기초해 계산된다. 위 그림처럼 RNN에서 뻗어나가는 값이 달라보이지만 실제로 출력이 분기하는(같은 값을 가지는) 형태이다.
RNN에서는 가중치가 2개 존재하는데 하나는 입력을 출력 h로 변환하기 위한 가중치 Wx이고, 다른하나는 출력으로 변환하기 위한 가중치 Wh이다.
여기서 순환신경망은 가중치를 모든 단계에서 공유한다.
가중치 공유를 통한 장점
- 순차 구조를 포착할 수 있다.
- 가변 길이 데이터를 처리하기 쉽다.
- 파라미터 수가 절약되고 정규화 효과가 생긴다.
BPTT(backpropagation through time ) - 시간펼침 역전파
먼저 한 계층에 위와 같이 4개의 노드가 있다고 할 때 Loss값은 각 단계의 손실 L1, L2, L3, L4 가 나올 것이다. 이때 회귀문제라면 MSE, 분류 문제라면 Cross Entropy를 사용한다.
위 식은 전체 손실함수를 나타낸 수식이다. BPTT의 순서를 살펴 보면
- 전체 손실함수 → y4 → h4 → x4,h3 → x3,h2→ x2,h1 → x1,h0 순서로 진행된다.
- 이때 가중치는 공유되기 때문에 같은 가중치가 업데이트 된다.
- 전체 손실함수 → y3 →h3 → x3,h2→ x2,h1 → x1,h0 이 과정은 y1까지 반복한다.i
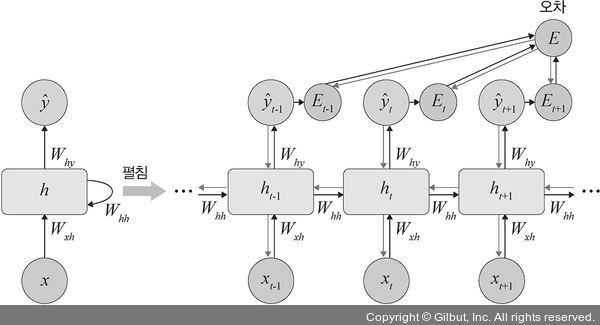
단점 :
- 시계열 데이터에서 시간적으로 멀리 떨어진, 장기 의존 관계를 잘 할습할 수 없다. → BPTT에서 기울기 소실 혹은 기울기 폭발이 발생한다.
LSTM(Long-Short Term Memory)
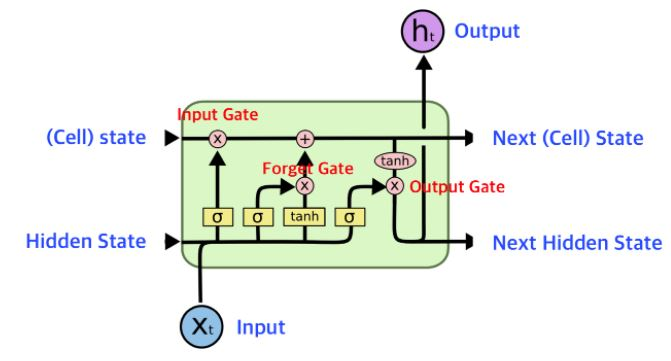
Cell state : 장기기억 H(Hidden state) : 단기기억 x : 입력값
기존 RNN의 문제에서 별도의 C경로를 두어 가중치 행렬곱 연산을 없앤 것이 특징이다. 이를 통해 순방향 흐름과 역방향 흐름이 원활해지면서 장기 의존성 문제와 그레디언트 소실 문제가 완화된다.
반면 H경로에는 행렬곱 연산을 남겨둬 순차 데이터를 처리하는 뉴련 연산을 가능하게 한다.
forget gate - 망각 게이트
장기 기억을 지속할지 잊을지 판단한다. 잊어도 되는 장기 기억은 망각 게이트를 통과하지 못한다.
gate gate - 기억 게이트
장기 기억을 새롭게 갱신하기 위해 망각 게이트를 통과한 장기 기억에 입력 게이트를 통과한 새로운 기억을 더한다.
input gate - 입력 게이트
새로운 사건으로 형성된 기억 중 장기 기억으로 전환해야 할 기억을 선택한다.
output gate - 출력 게이트
갱신된 장기 기억에서 갱신된 단기 기억에 필요한 기역을 선택한다.
cell state 연산
hidden state 연산
LSTM에서 그래디언트 소실이 생기지 않는 이유
장기기억인 cell state의 미분을 보면 알 수 있다.
위의 식에서 미분을 해보면
forget gate의 곱으로 만들어진다. 즉 연속적으로 W를 곱하지 않으므로 그레디언트 소실 발생가능성이 작아지게 된다.
GRU
GRU는 LSTM 장점을 유지하면서 게이트구조를 단순하게 만들었다.
cell state 대신 hidden state에 장단기 기억을 모두 넣었다.
r (reset gate) : 새로운 사건이 발생했을 때 기억을 새롭게 형성하기 위해 장기 기억과 단기 기억에서 필요한 부분을 선택한다.
z (update gate) : 기억을 갱신하기 위해 기존 기억과 새롭게 형성된 기억의 가중치 평균을 계산하는 기중치 역할
새로운 기억 생산
갱신된 기억 ht 계산
갱신된 기억인 은닉상태 ht는 이전상태 ht-1와 새로운 사건으로 형성된 기억의 가중평균으로 계산한다.
GRU는 LSTM에 비해 파라미터가 줄었지만 성능은 비슷하다.