신경망 학습 : 모델의 파라미터 값을 결정한다는 의미 → 모델 파라미터는 뉴런의 가중치와 편향
학습 : 훈련 데이터로부터 가중치 매개변수의 최적값을 자동으로 획득하는 것
손실함수 (Loss Function, Cost Function) : 알고리즘이 예측한 값과 실제 정답의 차이를 비교하기 위한 함수 → 최적화(Optimization)를 위해 최소화 하는 적이 목적인 함수
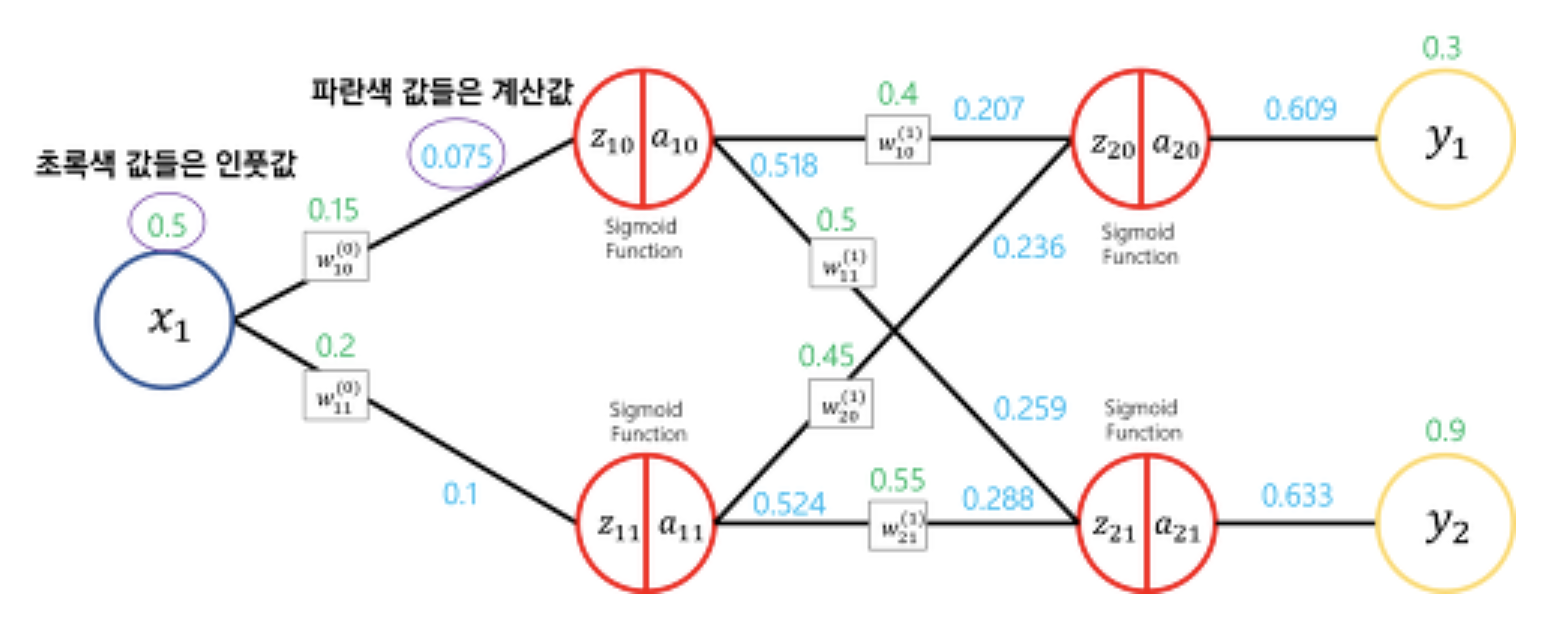
Image Reference : https://wooono.tistory.com/216
위 그림의 수식을 먼저 정리하면
위의 두 개 수식 정리 : z 는 직전 Layer n에서 m으로 가는 방향을 가질때 1번 Layer m번 째 Node를 표현한 식. → 직전 Node의 웨이트와 값의 곱과 전체 시그마로 표현 가능
밑에 Activation Function은 활성화 함수로 분류에는Sigmoid 와 Softmax 함수를 사용함. 이때 a를 다음 Node로 향하는 Weight(w)와 곱할 x값이라고 생각
위의 3개 수식 정리 : 직전 레이어 2에서 마지막 한개의 Node로 가는 것을 표현. 마지막 Node에는 Activation Function을 적용하는 것 이 아닌 Identity function을 사용해서 표현
마지막 식은 Loss function을 나타낸 식
최적화(Optimization) : 최적의 파라미터를 찾는 방법 (근사적으로 함수의 해를 찾음), Loss를 최소화 하는 해를 구함.
회귀 문제를 예로 보면 타깃과 예측값의 오차를 최소화하는 파라미터를 찾는 것
파라미터 : 수학과 통계학에서 어떠한 시스템이나 함수의 특정한 성질을 나타내는 변수.
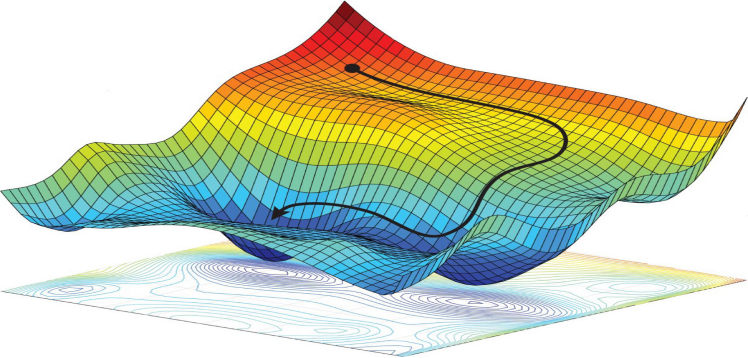
Image Reference : https://darkpgmr.tistory.com/149
최적화의 원리 : 현재 위치에서 함수값이 감소 하는 방향으로 조금씩 파라미터 값을 이동해 나가는 것. 가장 중요한 문제는 Local minima 문제와 어느 방향으로 내려갈 것인지, 얼마 만큼 이동할 것인지이다. Global minima에 다다르는 것이 최종 목표
최적화 알고리즘
SGD Momentum
- 특징 : 최적해에 진행하는 소곧에 관성을 주어 안장점에서 학습이 안되는 문제 해결
- 단점 : overshotting (최소점을 지나치게 되는 문제 발생)
AdaGrad
- 특징 : 학습률의 적응적 조절 - 가파른 곳에서는 천천히(학습률 낮음), 완만한 곳에서 빠르게 (학습률 높음)
- 단점 : 경사가 가파른 곳에서 학습이 시작되면 학습률이 급격히 감소해 중단될 수 있다.
RMSProp
- 특징 : 최근경로의 곡면 변화량에 따라 학습률 적응적 조절
- 단점 : 학습초기 경로가 편향됨 -
Adam
- 특징 : 진행하던 속도의 관성과 동시에 곡면 변화량에 적응적 학습률을 갖는 알고리즘, 초기 가중치 편향(학습률이 급격하게 올르는 것) 을 해결함.
