Fourier Transform

1. Fourier Transform

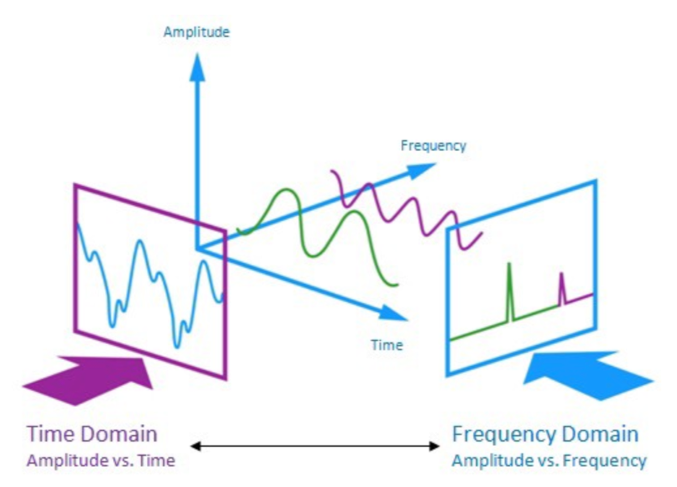
Fourier Transform 이란 입력신호(audio signal)를 sin, cos의 주기함수 성분으로 분해하는 것을 뜻한다.

여기서 주기함수 성분들은 각각 고유의 frequency(주파수)와 amplitude(강도)를 갖고 있다.

위에 그림을 보면 두 개의 simple wave(단순파)가 time domain에서 complex wave(복합파)로 표현되고 있다. 여기에 Fourier Transform을 실시하면 주파수 도메인에서 두개의 주파수 성분으로 분해할 수 있다.

(1) $f(x) = ∫^{∞}_{-∞}F(k)e^{jiπkx}dx$ : inverse FT
(2) $F(k) = ∫^{∞}_{-∞}f(x)e^{-jiπkx}dk$ : FT

(1) 입력신호 $f(x)$를 모든 가능한 주파수(k)의 주기함수들 $e^{jiπkx}$의 일차결합으로 표현한 것이다.
(2) $f(x)$를 주기함수 성분으로 분해했을 때의 계수 $F(k)$.
입력신호 $f(x)$를 기저함수로 분해했을 때의 계수 $F(k)$는 $f(x)$와 기저함수의 내적(dot product)으로 계산될 수 있다.

($f(x)$: 입력신호, $e^{jiπkx}$: 주기함수 성분, $F(k)$: 해당 주기함수의 강도(amplitude))

** $F(k)$를 구하는 방식은 선형대수학(linear algebra)을 통해 이해해볼 수 있다. linear algebra에서는 어떤 벡터 공간을 생성할 수 있는 일차독립인 벡터들의 집합을 기저(basis)라고 한다. 벡터공간 V = a1v1 + a2v2 + a3v3 + .. + anvn 와 같이 기저 벡터들의 일차결합으로 표현될 수 있다.
만일 기저벡터들이 서로 수직 vi・vj = 0 (=orthogonal)인 단위벡터라면 일차결합 계수 ai는 ai=v・vi=(a1v1+a2v2+..+anvn)vi로 손쉽게 계산할 수 있다.

2. Discrete Fourier Transform(DFT)

이산 푸리에 변환은 특정 도메인(예컨대 시간)의 이산 신호(discrete signal)를 다른 도메인(예컨대 주파수)의 이산 신호로 변환하는 과정이다. 여기에서 이산이란 연속(continuous)과 반대되는 말로써 신호의 값이 연속적이지 않고 띄엄띄엄 있어서 이것들을 제외한 시간이나 주파수에서는 값이 0인 것을 뜻한다/

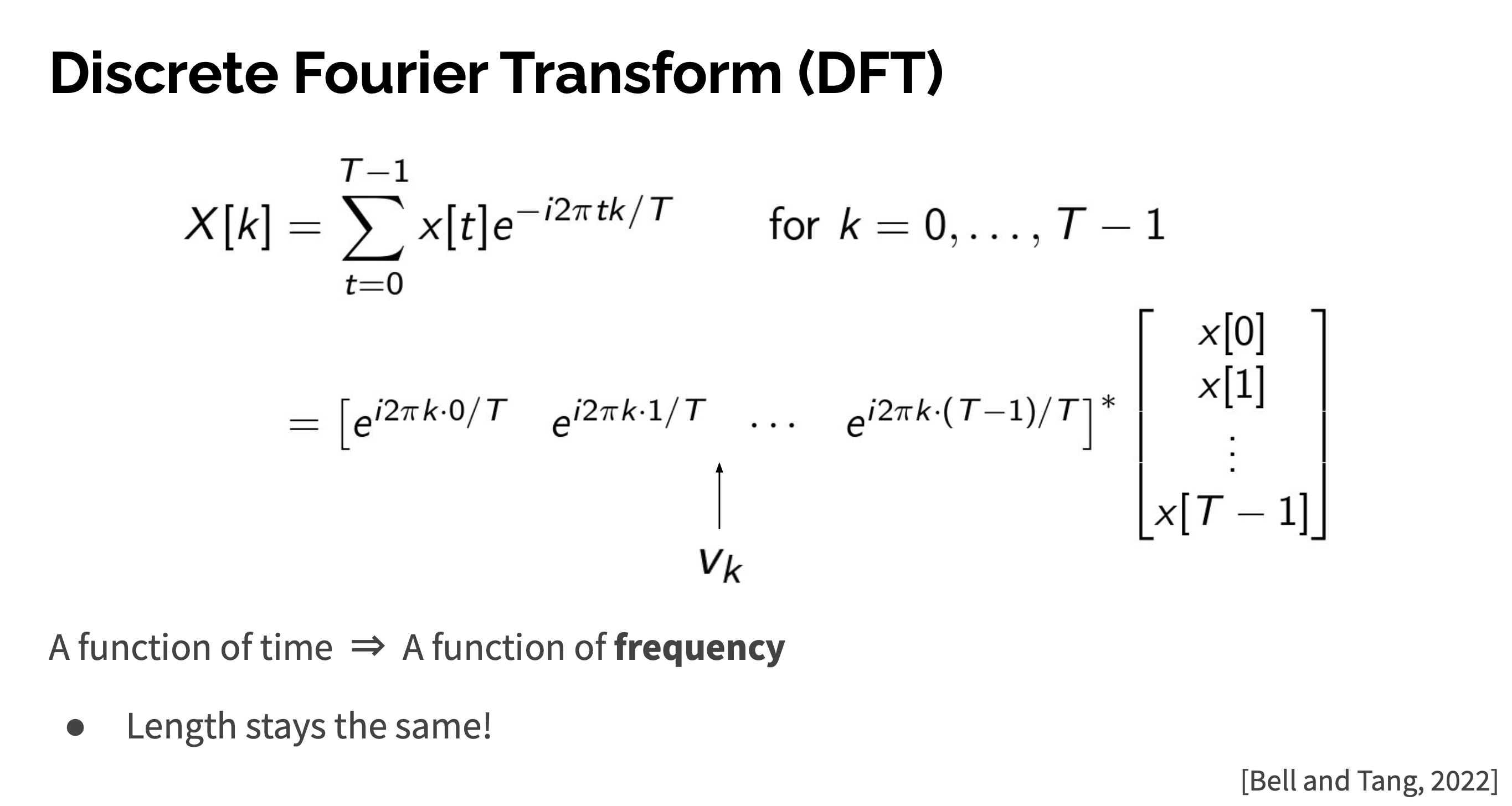
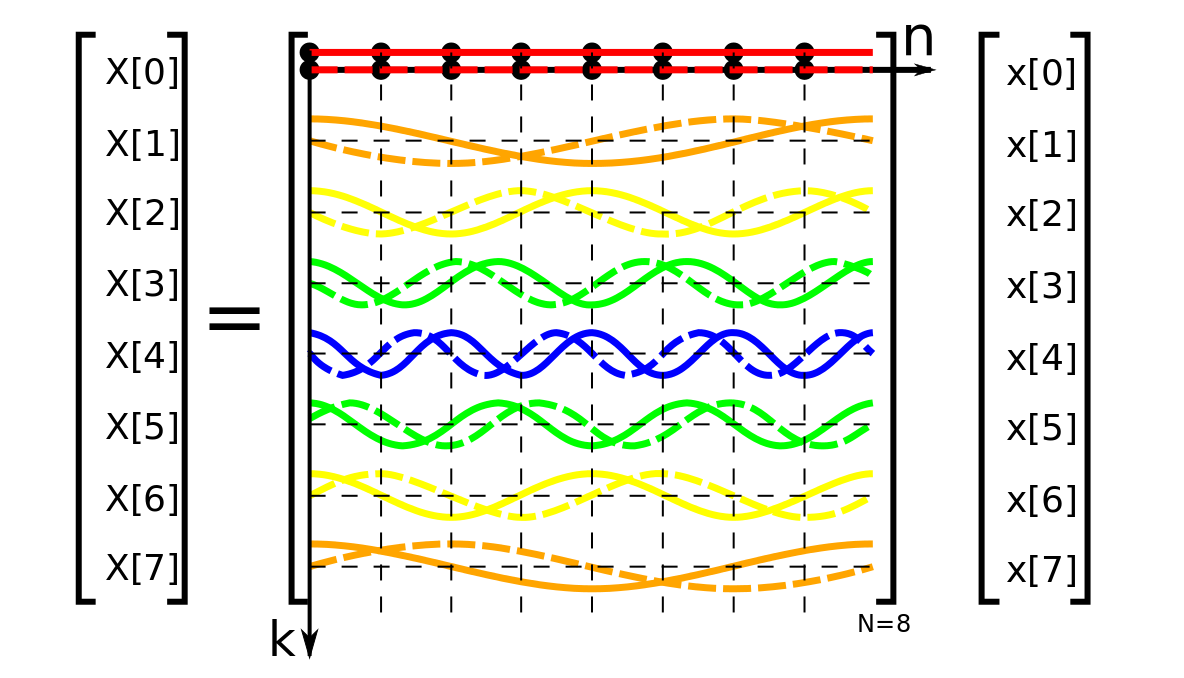
$v_{K}$ = frequency k인 주기함수 성분
즉 DFT는 입력신호에 대해 linear transformation을 해주는 것.

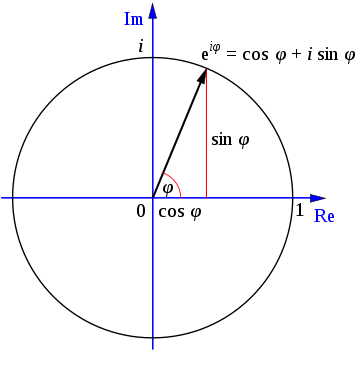
** 오일러 공식
= $Σ^{T-1}_{t=0}x_{n}[cos((2π/T)kt) - isin((2π/T)kt)]$

정리
(1) $X[k]$ is a complex number
(2) $X[k]$ is a (complex) dot product of a complex sinusoid $v_{k}$ and the signal x
- sinusoid:
(3) $X[k]$ tells us how similar x is to $v_{k}$
(4) The large k's in X are high-frequency components, while the small k's in X are low-frequency components

• 참고: https://ratsgo.github.io/speechbook/docs/fe/ft
• 참고: https://darkpgmr.tistory.com/171