Smoothing

1. Add-1

$P_{Add-1}(w_{i}|w_{i-1}) = [c(w_{i},w_{i-1}) +1] / [c(w_{i-1}) + V]$

2. Add-k

$P_{Add-k}(w_{i}|w_{i-1}) = [c(w_{i},w_{i-1}) +k] / [c(w_{i-1}) + kV]$
or
$P_{Add-k}(w_{i}|w_{i-1}) = [c(w_{i},w_{i-1}) + m(1/V)] / [c(w_{i-1}) + m]$

3. UnigramPrior

$P_{UnigramPrior}(w_{i}|w_{i-1}) = [c(w_{i},w_{i-1}) + mP(w_{i})] / [c(w_{i-1}) + m]$

<Advanced smoothing algorithm>
Use the count of things we've seen once
- to help estimate the count of things we've never seen

• Good-Turing
• Kneser-Ney
• Written-Bell

4. Good-Turing

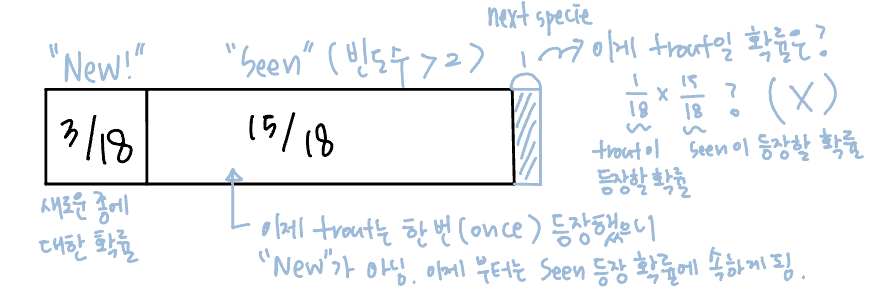
How likely is that next species is trout?이 1/18보다 더 낮아지는 이유는?
빈도수가 1인 물고기들이 (빈도수 2에 비해)많으면, 새로운 물고기(지금까지 Unseen된 물고기)가 나올 확률이 지금 한 번 등장한 물고기가 또 나올 확률보다 더 높다는 것이다. 즉, 빈도수가 1인 물고기들이 다시 (다시 등장하면 빈도수가 2가됨) 등장할 확률은 낮아지는 것($1\over18$보다 더 낮아지는 이유).

단순하게 MLE방법을 사용하면 위에서 trout의 확률로 $1\over18$을 예상할 수 있지만, 새로운 종에 대한 확률(추정치) $3\over18$도 고려를 해주어야 한다.

그러면, $1\over18$로 예측했던 추정치는 $1\over18$ 미만으로 줄어든다.

그러면 이 줄어드는 확률은 어떤 식으로 반영을 해주어야 될까?

$1\over18$ * $15\over18$ ?? 일 것 같지만 아니다.
위에서는 3개의 new-species가 있지만, 여러 가지를 고려했을 때 3개보다 더 높게 반영해야할 수도 있기때문에 이렇게 단순하게 확률을 구해서는 안된다.

위에 c*를 구하는 식을 뜯어보자.
fish species가 $N_{2}$ < $N_{1}$ 이니 1번 등장했던게 또(c+1) 등장할 확률을 1(=c)번째 등장 확률보다 줄어든다는 것을 표현한 식이다.

ex. 귤, 사과 / 두부, 두부, 만두, 만두 / 말, 말, 말, 곰, 곰, 곰, 책, 책, 책 = 총 15번
$N_{1}$ = 2
$N_{2}$ = 2
$N_{3}$ = 3
현재 두부의 확률은 2번/15번 = $2\over15$
만약 다음에 또 두부가 나올 확률은?
$N_{2}$ < $N_{3}$ 이니깐 위에 예시와는 반대로 또 등장할 확률이 더 높아진다.

c* = $\frac{(2+1)N_{3}}{N_{2}}$ = $\frac{(2+1)3}{2}$ = $\frac{9}{2}$ = Adjusted count

$P'_{두부}$ = $\frac{2}{15}$ -> $\frac{\frac{9}{2}}{15}$ = $\frac{9}{30}$ = $\frac{3}{10}$