0. HMM
HMM은 observation(관측치) 뒤에 hidden(은닉)되어 있는 state(상태)를 추청하는 것이다. 즉, 우리가 보유하고 있는 observation(데이터)는 true hidden state(실제 은닉 상태들)이 노이즈가 낀 형태로 실현된 것이라고 보는 것이다. 이러한 모델링 기법은 noisy channel이라고 한다.
ex. P(x=아이스크림 구매|q=더운 날씨)
그렇다면 ASR에서 HMM이 필요한 이유는 무엇일까?
사람마다 같은 단어를 말하더라도 pronounciation과 accent가 다 다르다. 또 같은 사람이 말하더라도 1분전에 말한 '안녕'과 1분후에 말한 '안녕'의 acoustic signal은 조금이라도 다를 것이다. 말의 세기, 속도, 높낮이 등을 로봇이 아닌 이상 그대로 재현하기란 어렵기 때문이다. 그래서 spectrogram()은 각각의 사람마다 심지어 같은사람이라도 말할 때마다 다른 모양을 띄게 된다. 하지만 acoustic signal -정해지지 않은 말소리-가 다 다르다고 하더라도 이 acoustic signal이 표현하고자 했던 어떠한 phone(음운)-인간이 공유하는 언어-이 있을 것이다.

또 그렇다면 하나의 phone을 표현한 acoustic signal은 단 하나의 acoutic trend만을 가지고 있을까? 아니다. 하나의 phone을 표현할 수 있는 몇가지의 phone states가 존재할 수 있다. 그래서 어떤 사람이 이 phone을 이 몇가지의 phone states 중 하나의 방식으로 표현하고자 했고 그래서 음성으로 어떻게 나왔다면 결국 는 에 영향을 받아 만들어진 소리일 것이다.
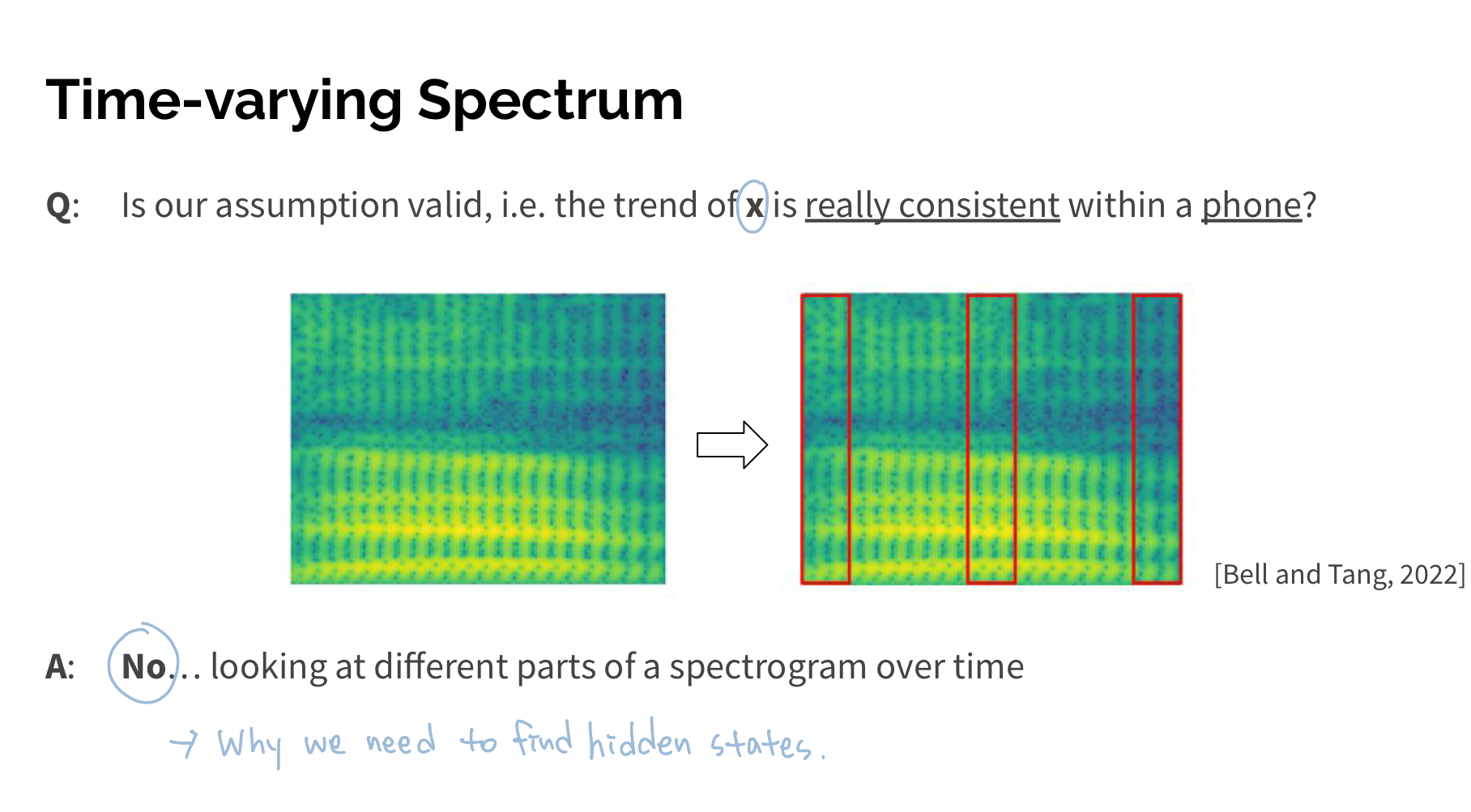
그래서 우리는 아래와 같이 비정형의 acoustic signal에 몇가지 정형화된 phone states를 지정해줄 수 있다.
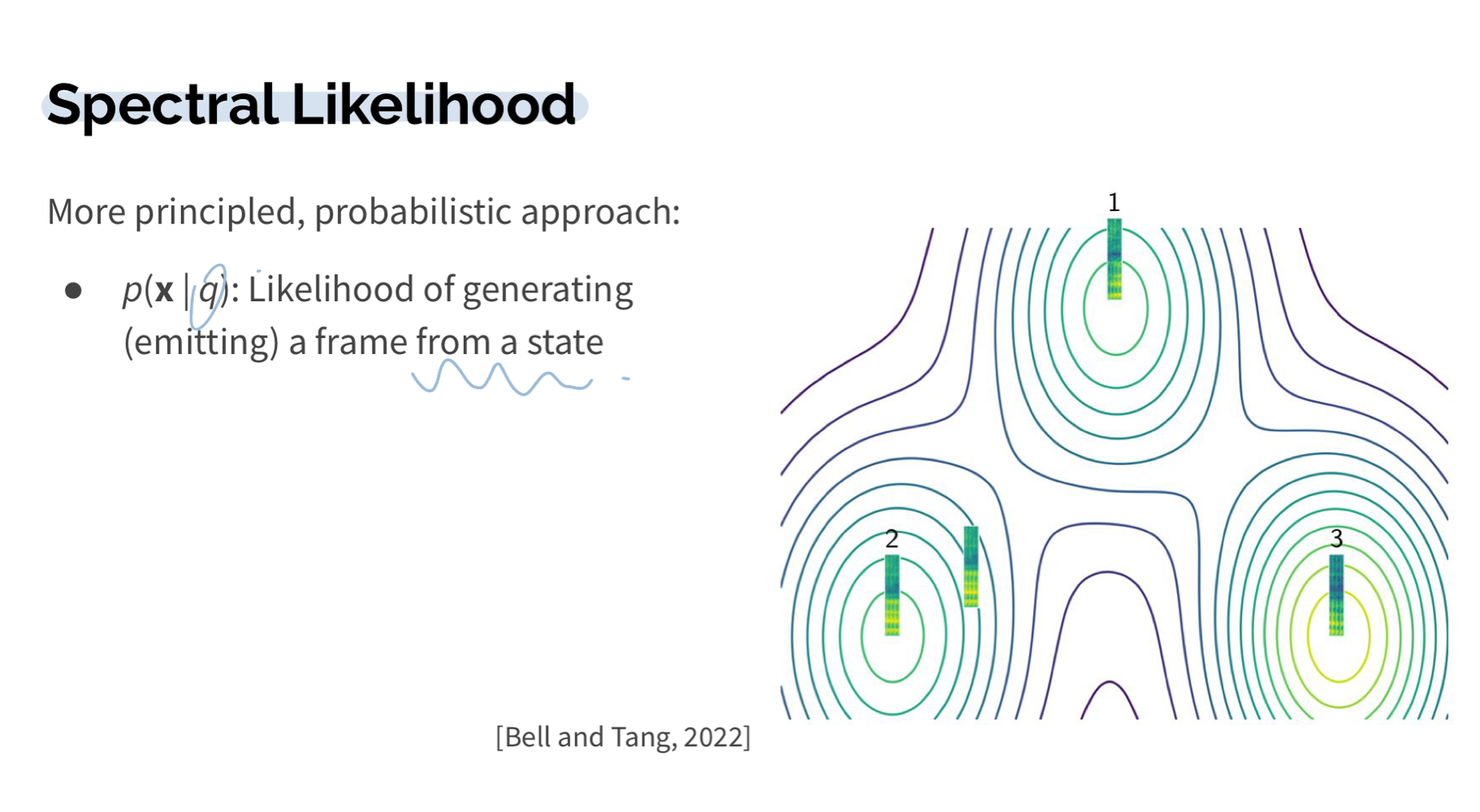

결국, = (=phone, s, 에서 발생할 수 있는 가능한 hidden state) + noisy channel(각각의 사람마다 특유의 accent와 숨소리, 발성 등등)으로 나타낼 수 있다.
HMM Assumption
1) State depends only on the preceding state
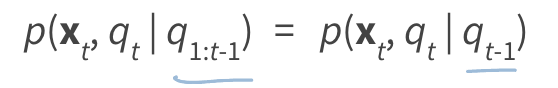
2) Observation depends only on the current state
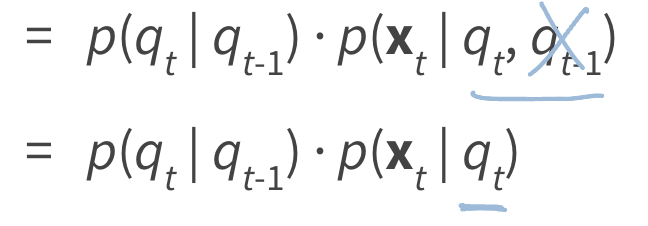
1. Likelihood
Likelihood란 모델(λ)을 이용해 observation sequence 가 나타날 확률을 구하는 것.
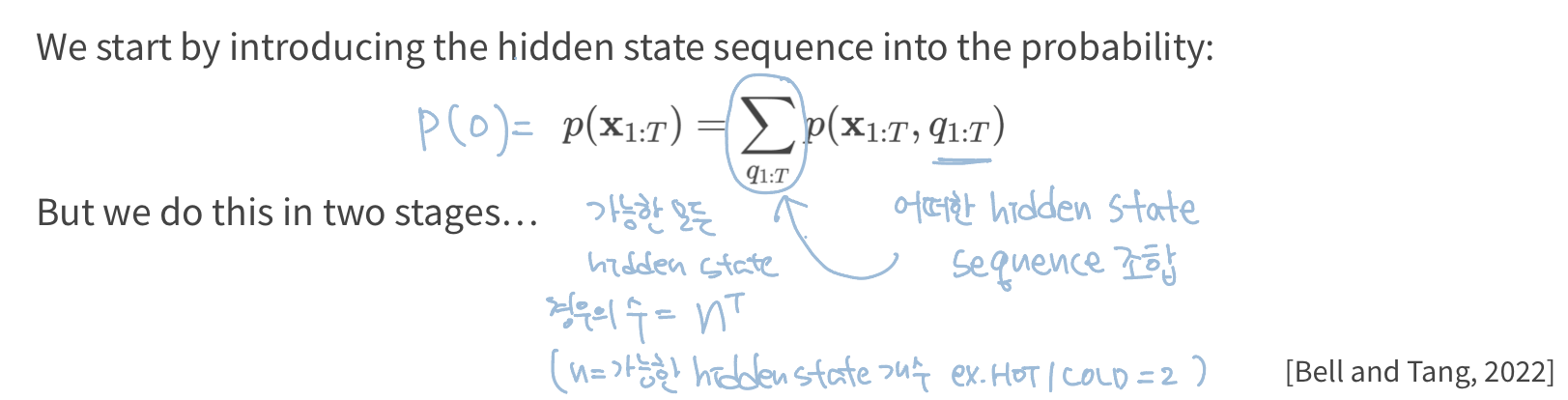
즉, '가 특정 hidden state sequence()에서 발생한 확률'을 모든 hidden state sequence에 대해서 더해주면 observation sequence()가 나타날 확률을 구할 수 있다.
예를 들어보자,
만약 10년 전 아이스크림 소비 개수가 3일 간 = [3개, 1개, 3개]라고 해보자. 총 3일 간 각 이 아이스크림의 소비를 유발하는 hidden state 인 날씨는 날짜별로 HOT일 수도 있고 COLD일 수도있다. 따라서 총 의 경우의 수가 존재한다. 이 각각의 경우에서 observation sequence가 발생하는 확률(=총 8개의 probability)을 더해주면 된다.
Computation(계산)을 표로 나타내면 다음과 같다.

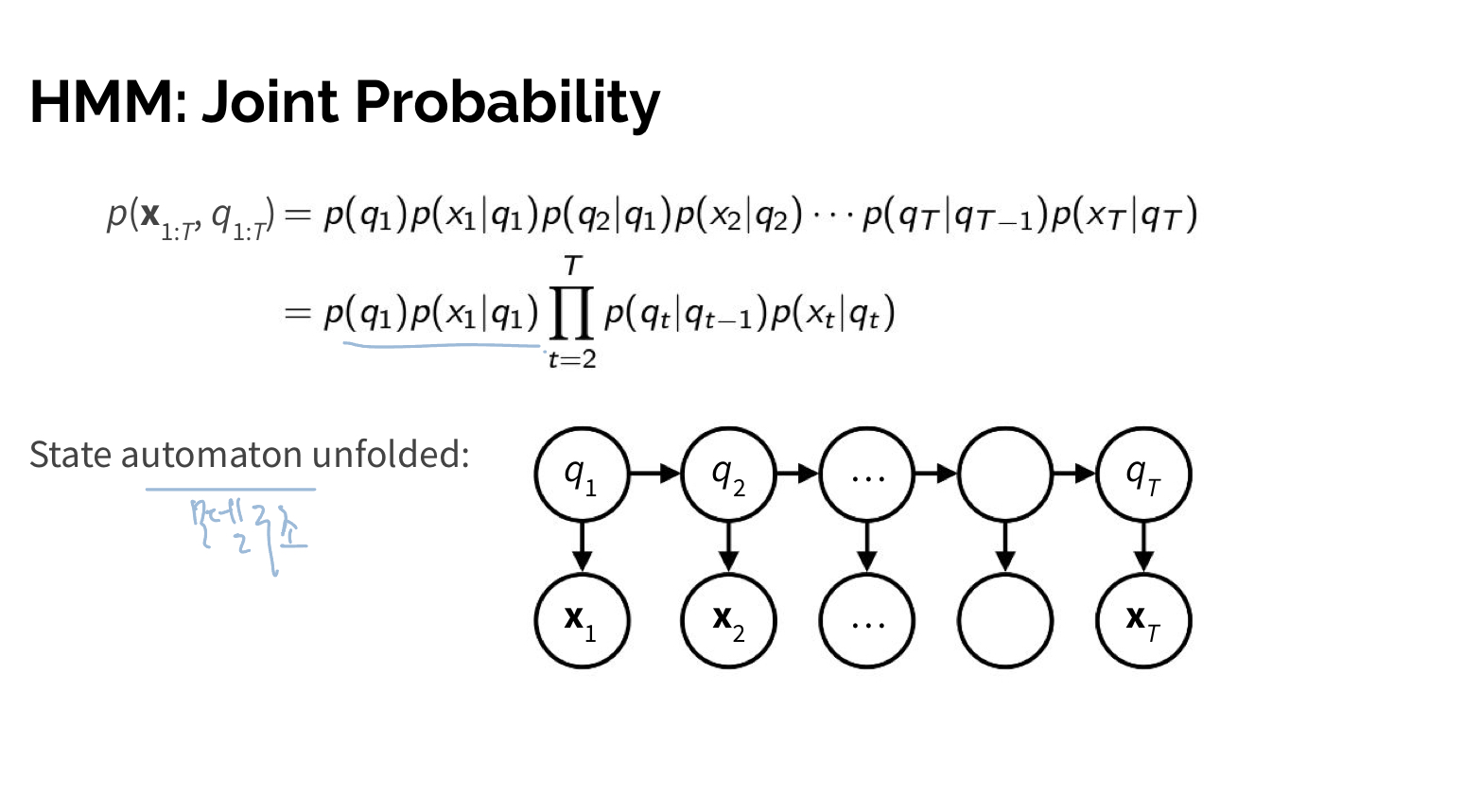
여기서 joint probability는 Hidden Markov chain 공식을 이용해 구해준다. observation sequence()와 특정 hidden state sequence의 joint probability는 '0.HMM' 위에서 설명했던 HMM Assumption을 적용해 다음과 같이 구할 수 있다.
Forward/Backward Algorithm
하지만 위와 같이 모든 경우의 수대로 likelihood를 구하면 hidden state가 N개, observation이 T개일 때, time complexity가 이 된다. 이러한 비효율성을 줄이기 위해 dynamic programming기법이 사용된다. dynamic programming이란 중복되는 계산을 저장해 두었다가 나중에 다시 사용하여 계산을 줄여준다.
Forward Alogrithm: Likelihood를 계산할 때 시간 순으로 dynamic programming 적용
Backward Algorithm: Likelihood를 계산할 때 시간의 역순으로 적용
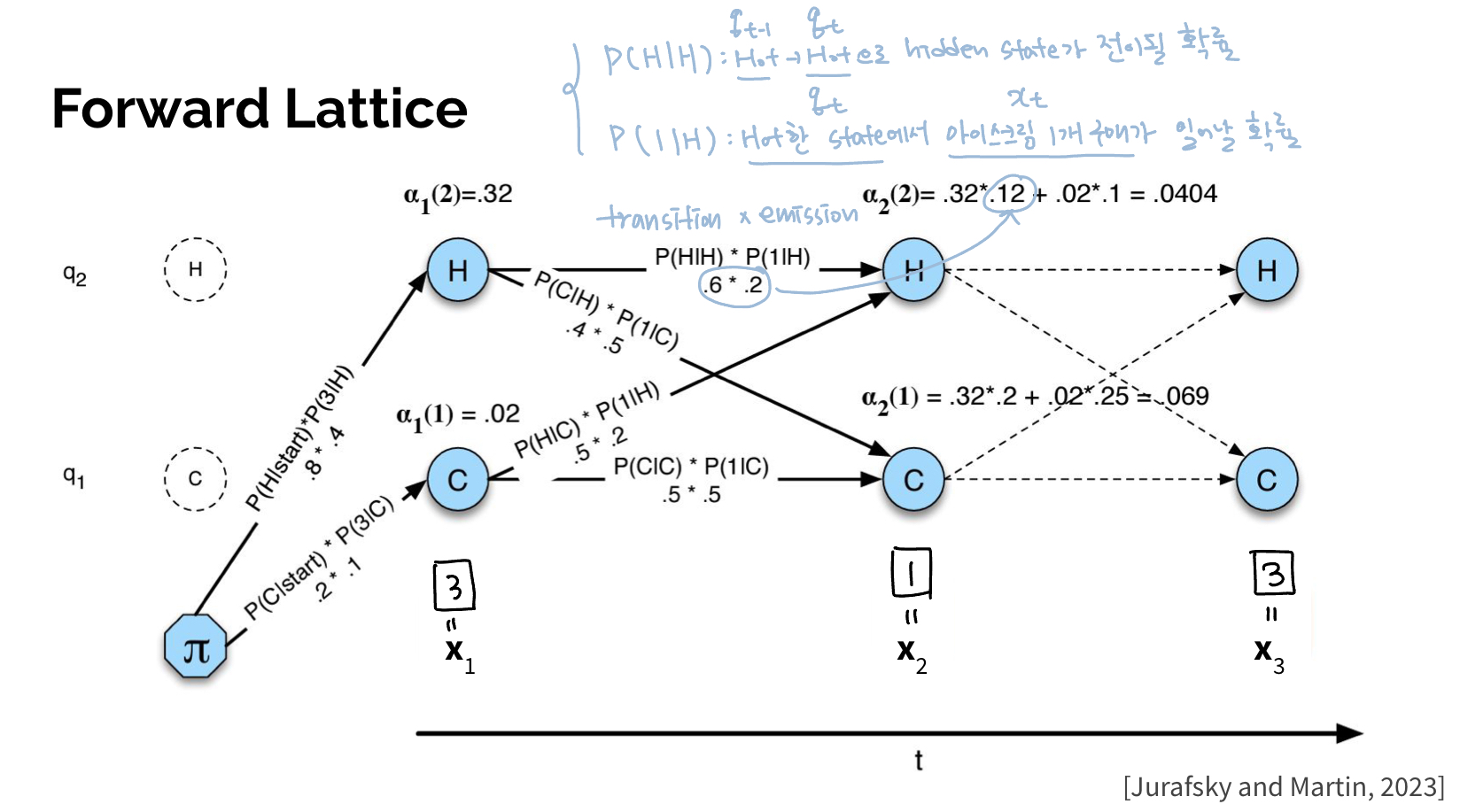

Sum of all components(values) coming from previous nodes.
2. Decoding
모델 λ과 observation sequence 가 주어졌을 때 가장 확률이 높은 hidden state sequence()를 찾는 것.
Forward Algorithm vs Viterbi Algorithm
그냥 Forward Algorithm과 Viterbi Algorithm의 가장 큰 차이점은 Viterbi에는 backtracking(역추적) 과정이 있다는 점이다. 각각의 Algorithm 사용 목적을 보면 다른 이유를 확인할 수 있다.
Likelihood Computation은 무엇을 찾거나 예측하는 것이 아니라 Observation이 나타날 확률을 계산하는 것이다. 따라서 Forward Algorithm과 같이 모든 가능한 hidden state에 따른 관측지가 나타날 probability를 모두 더해주는 것이다.
이와 달리, Decoding의 가장 큰 목적은 모델 λ과 Observation이 주어졌을 때, 가장 확률이 높은 hidden state sequence(best path) Q를 찾는(예측하는) 것이다.(음성인식에서는 각 hidden state에 phones이 들어가 있으므로, 관측값인 특정 음성 신호(O ; MFCC)를 가지고 best phones sequence를 찾는 과정을 의미한다.) 따라서 1) 각각의 path의 확률을 계산하고 2) 그 다음 backtracking을 통해 그 중에서 가장 확률이 높은 hidden state sequence를 선택해주면 된다.
코딩은 모델과 관측 시퀀스 O가 주어졌을 때 hidden state Q의 best path를 찾는 과정이다. 음성인식에서는 각 hidden state에 phones이 들어가 있으므로, 관측값인 특정 음성 신호(O ; MFCC)를 가지고 best phones sequence를 찾는 과정을 의미한다.
1) Computing Paths
Viterbi Path Probability

Viterbi Path Probability를 구하는 formula는 다음과 같다.

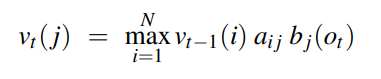
2) Backtracking
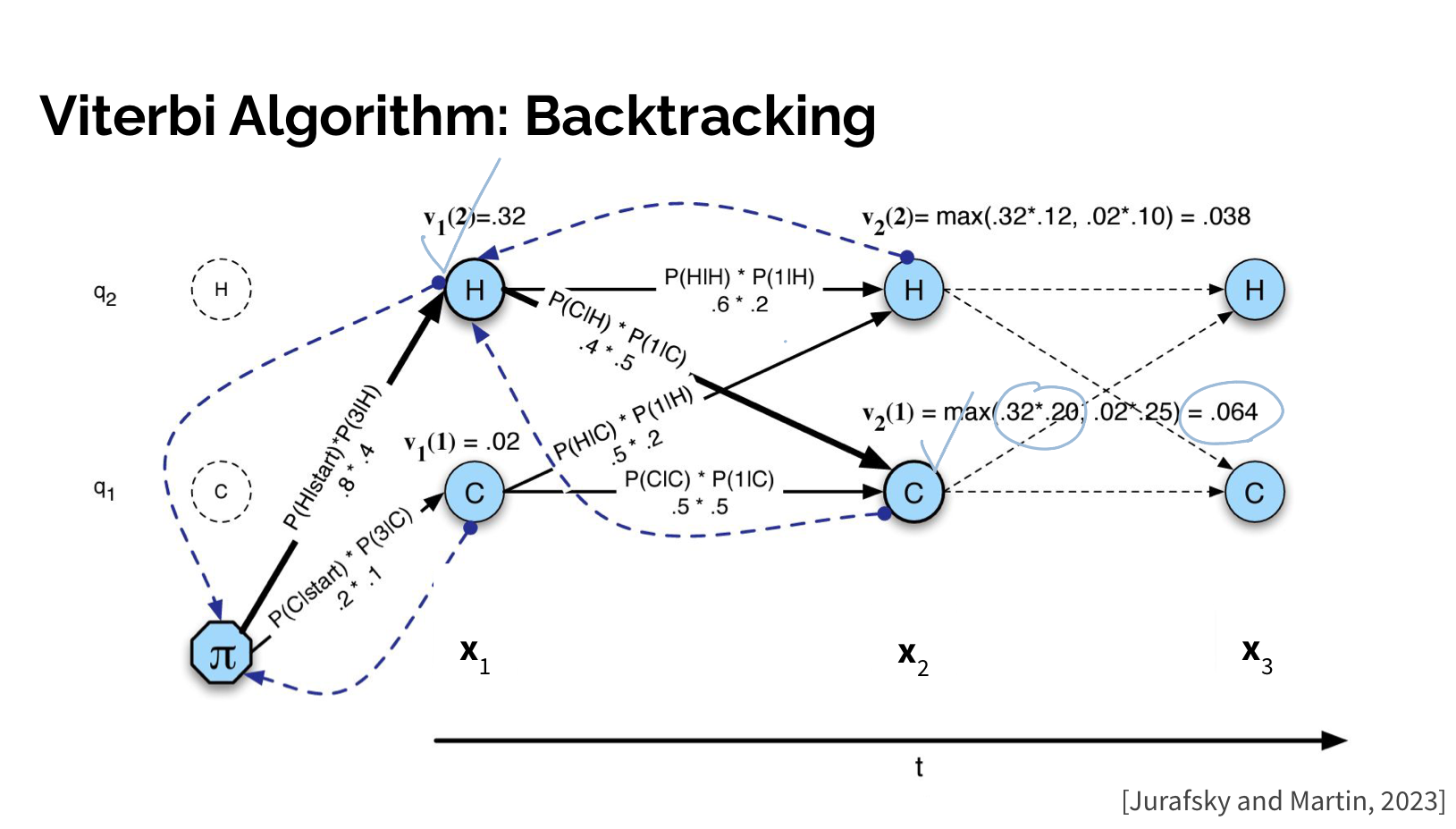

3. Training
decoding에서 구한 best path hidden state Q와 관측값 O를 가지고 HMM 파라미터인 A(transition prob), B(emission prob)를 학습(추정)하는 과정이다.
