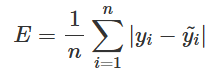
Loss Function

 신경망 학습은 최적의 매개변수 값을 찾는 과정으로, 이 과정에서 손실 함수가 사용된다. 손실 함수를 사용하면, 예측값과 실제값 사이의 차이(loss)가 최소가 되는 방향으로 학습시키면서 최적의 매개변수를 찾아낼 수 있기 때문이다.

 대표적인 손실 함수엔 Mean Squared Error(MSE)와 Cross Entropy Error(CEE)가 있으며, 일반적으로 MSE는 회귀 문제에, Cross Entorpy는 분류 문제에 사용되는 것으로 알려져 있다.

 이렇게 대충 이해하고 넘어갈 수도 있지만, 이렇게 얕게 이해하고 넘어가는 것보다 어떤 이유에서 이런 말이 나오는지 알아보는 것도 중요하기 때문에 오늘은 왜 연속적인 분포를 갖는 데이터(ex. 회귀 문제)엔 MSE를 사용하는 것이 좋은지, 이산적인 분포를 지니는 데이터(ex. 분류 문제)엔 왜 CEE를 사용하는 것이 좋은지 그 이유에 대해 알아볼 것이다.

Mean Squared Error (MSE)

 MSE는 실제값과 예측값 사이의 차이(loss)를 제곱한 값으로, 아래와 같은 식으로 정의된다.

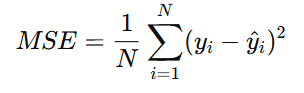
 MSE는 오차 값을 제곱하므로 음수 값의 영향을 받지 않고, 큰 오차에 더 많은 패널티를 줄 수 있다. 또한, 오차값이 상대적으로 크게 반영된다는 특징이 있다.

 이처럼 MSE는 예측 값과 실제 값 사이의 연속적인 수치 차이를 직접적으로 다루는 데 적합하며, 이러한 차이에 민감하다는 특성이 있어 오차가 큰 예측값을 빠르게 수정하도록 유도할 수 있다는 장점이 있다. 손실 함수를 사용하는 목적은 예측값과 실제값 차이(loss)가 최소가 되는 값을 찾는 것이 목표인데, 이를 통해 가중치를 업데이트하면 보다 더 빠르게 목표에 도달할 수 있다.

 따라서, MSE는 회귀와 같이 연속적인 숫자 값을 예측하는 문제(ex. 집값/기온/매출 예측)에 적합하다.

Cross Entropy Error (CEE)

 CEE는 아래와 같은 식으로 정의되며, 예측값과 실제값 사이의 확률 분포 차이를 계산한다.

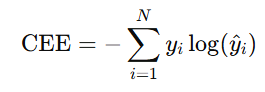
 이때, $y_i$는 주로 one-hot 벡터이기 때문에 실제 정답에 해당하는 $y_i=1$인 경우에만 loss에 영향을 주고, 다른 클래스는 loss에 영향을 주지 않는다.

 또한, 정답인 확률이 높을수록 작은 loss 값을 지니기 때문에 예측값이 실제 정답과 얼마나 가까운지를 확률적으로 측정하기 좋고, 이를 통해 실제 정답의 확률을 높이고, 나머지 클래스의 확률을 낮추는 방향으로 가중치 업데이트를 진행하기도 좋다. 그래서 여러 클래스 중 어떤 클래스의 확률이 가장 높은지를 결정하는 분류 문제에 CEE를 사용하는 것이 적합하다.

---

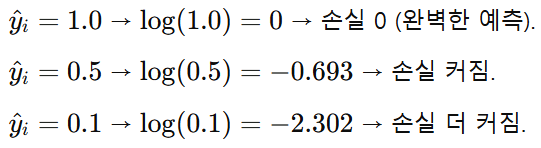
 정리해 보면, MSE는 실제값과 예측값 사이의 오차를 잘 반영하기 때문에 연속적인 값을 잘 다루는 회귀 문제에, CEE는 실제값(주로 one-hot 인코딩)과 예측값(softmax 혹은 sigmoid를 통해 나온 예측값) 사이의 확률 분포를 계산하기 때문에 분류 문제에 주로 사용된다.

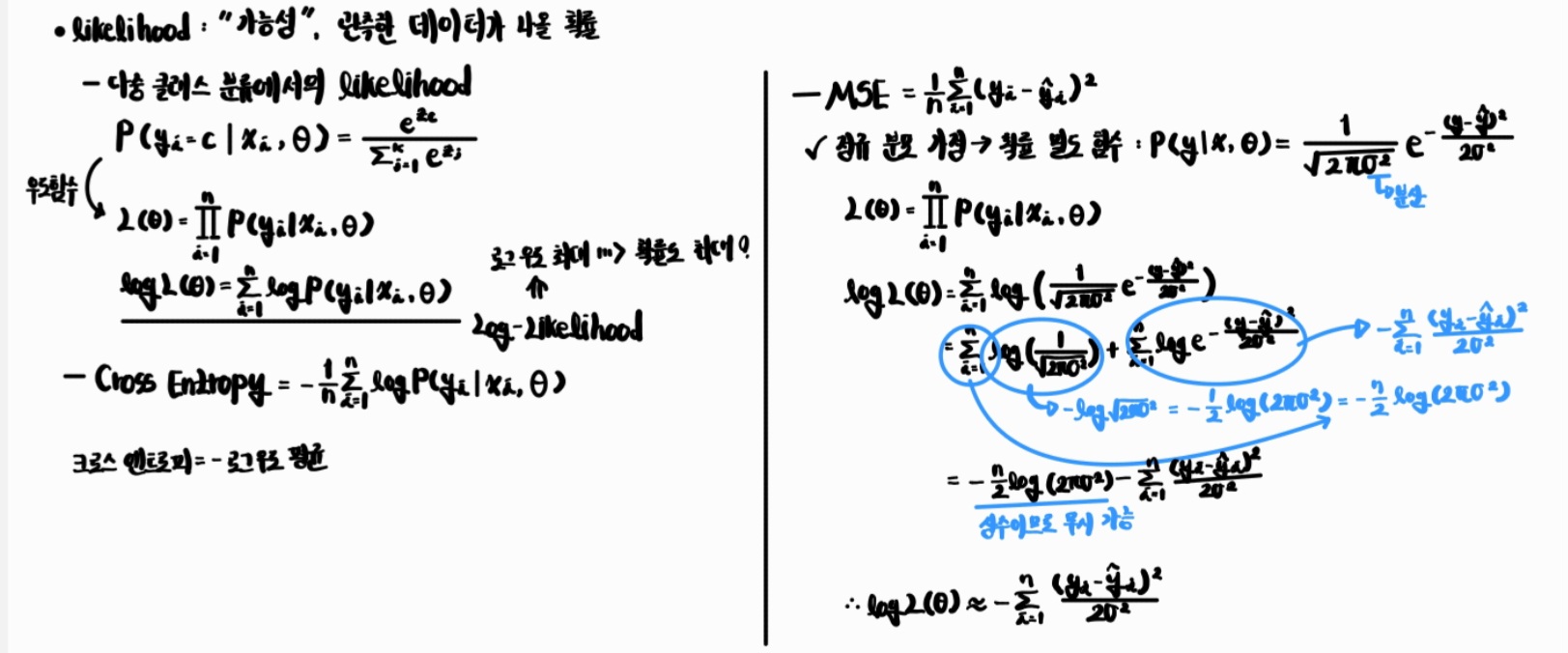
• MSE = “정규분포 가정” 아래 로그우도를 최대화하는 손실

• CEE = “베르누이/이항(또는 다항) 분포 가정” 아래 로그우도를 최대화하는 손실
  

  
  
  
  

참고 - Regression vs Classification

회귀 분석 (Regression Analysis)

• 2개 또는 그 이상의 변수(독립 변수)들의 의존 관계를 파악함으로써 특정 변수(종속 변수)의 값을 예측하는 통계학의 한 분야
• 선형 회귀 분석 (Linear Regression Analysis) : 두 변수 x, y에 대한 n개의 측정값 (x1, y1), (x2, y2), ..., (xn, yn)이 있을 때 주어진 가설에 대한 비용이 최소화되도록 하는 선을 찾는 문제
  • $H(x) = Wx + b$
  • $cost(W, b) = \frac{1}{m} \sum_{i=1}^{m} (H(x^i) - y^i)^2$
  • cost(W, b)를 최소화하는 W, b를 찾는 문제 = Linear Regression
• 선형 회귀(Linear Regression)는 입력 값으로 사용하는 독립 변수 X와 출력 값을 의미하는 종속 변수 Y 사이 관계를 선형 함수식으로 모델링해 나타내며, 하나 이상의 독립 변수를 통해 연속적인 종속 변수를 예측한다.
• Non-linear Func, Curve, Parabola 등을 사용하지 않고, Linear Regression를 사용하는 이유는, 상대적으로 쉽고 간결하게 표현할 수 있기 때문임. 또한, Linear Regression이 더 복잡한 Non-linear 모델을 얻기 위한 토대가 되는 선으로 사용되기도 함. (Polynomial Regression)
• 데이터를 잘 설명하는 선을 선을 찾는 것 = Regression & Regression에서 예측하는 변수는 연속적이고, 양적 데이터(quantitative data, 숫자로 표현되고 수학적 계산이 가능한 데이터)임.

간단한 선형 회귀 구현 예시

• 아래의 코드에서 w, b의 Gradient는 다음과 같은 식에 의해 계산된다. (w, b에 대한 편미분 값 = Gradient)
  $\frac{\partial L}{\partial w} = \frac{2}{m} \sum_{i=1}^{m} (h(x^{(i)}) - y^{(i)})x^{(i)}$

• w, b update
  $w = w - \alpha \frac{2}{m} \sum_{i=1}^{m} (h(x^{(i)}) - y^{(i)})x^{(i)}$

# 단순한 선형 회귀 구현 예시
import numpy as np

# x, y가 완벽한 선형 관계(x=y)를 이루므로 학습이 잘 되면 w는 1에, b는 0에 근사해야 함.
x_train = np.array([1., 2., 3., 4., 5.])
y_train = np.array([1., 2., 3., 4., 5.])

# 초기 가중치 W, b 부여 (랜덤 값으로 W, b 초기값 지정)
W = np.random.random()
b = np.random.random()
print("initial weights : ", W, b)

n_data = len(x_train) # 데이터의 개수
epochs = 5000 # 반복 횟수
learning_rate = 0.01 # 학습률

for i in range(epochs):
hypothesis = x_train * W + b # 가설 H(x) = Wx + b
# 비용 함수 계산 cost(W, b) = \frac{1}{m} \sum_{i=1}^{m} (H(x^i) - y^i)^2
cost = np.sum((hypothesis - y_train) ** 2)
gradient_w = np.sum((W * x_train + b - y_train) * 2 * x_train) / n_data # gradient_w = \frac{2}{m} \sum_{i=1}^{m} (h(x^{(i)}) - y^{(i)})x^{(i)}
gradient_b = np.sum((W * x_train + b - y_train) * 2) / n_data # gradient_b = b = b - \alpha \frac{2}{m} \sum_{i=1}^{m} (h(x^{(i)}) - y^{(i)})

# w = w - \alpha \frac{2}{m} \sum_{i=1}^{m} (h(x^{(i)}) - y^{(i)})x^{(i)}
# b = b - \alpha \frac{2}{m} \sum_{i=1}^{m} (h(x^{(i)}) - y^{(i)})
W -= learning_rate * gradient_w
b -= learning_rate * gradient_b

if i % 500 == 0: # 500에폭마다 손실함수, w, b 값 출력
  print("Epoch ({:10d}/{:10d}) cost : {:10f}, W : {:10f}, b : {:10f}".format(i, epochs, cost, W, b))

# 최종 결과 예측
print("W : {:10f}".format(W))
print("b : {:10f}".format(b))
print("result : ")
print(x_train * W + b)

분류 (Classification)

• 독립변수 값이 주어졌을 때, 그 값과 연관성이 가장 큰 종속 변수(범주 또는 클래스)를 예측하는 문제, 다시 말해 어떤 표본에 대한 데이터가 주어졌을 때 그 표본이 어떤 범주 혹은 클래스에 속하는지를 알아내는 문제로, 예측하고 싶은 종속 변수가 범주형 데이터일 때 사용함.
• discrete category(or categories)를 예측함. (회귀와는 달리 유한하고 제한된 output categories를 지니며, 이산값(0/1)을 가질 수 있다)

분류 모형의 종류

1. 확률적 모형

• 각 카테고리 혹은 클래스가 정답일 조건부 확률(conditional probability)을 계산하는 모형
• 다시 말해, 입력 데이터 x가 주어졌을 때, 각 클래스가 정답일 확률 P(y|x) 을 계산하고, 이 중에서 가장 확률이 큰 클래스를 선택함.
• 각 클래스가 정답일 확률을 계산함.

확률적 생성 모형

• 확률 분포 P(x|y = k) 을 추정한 다음 베이즈 정리를 사용하여 P(y = k|x)를 계산하는 방법
• 조건부 확률 P(y|x)를 구하기 위해 각 클래스 y=k가 데이터를 만들 확률 분포 likelihood P(x|y)를 구하고 베이즈 정리를 사용해 조건부 확률을 계산함.
• (ex) Naive Bayes Classifier, Linear Discriminant Analysis 등
• 클래스가 많을 경우, 모든 클래스에 대해 추정해야 하므로 계산량이 너무 많이 필요하다는 단점이 존재함.

import numpy as np
import matplotlib.pyplot as plt

X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]]) # 2차원 좌표 데이터
y = np.array([0,0,0,1,1,1]) # 각 점의 클래스
# y = 0 표시
plt.scatter(X[:3, 0], X[:3, 1], c="k", s=50, edgecolor='k', linewidth=2, label="y=0")
# y = 1 표시
plt.scatter(X[3:, 0], X[3:, 1], c="w", s=50, edgecolor='k', linewidth=2, label="y=1")

# test data (빨간색 x로 표시)
plt.scatter(-0.2, -0.1, c='r', s=100, marker='x', edgecolor='k', linewidth=2)
plt.xlabel("x1")
plt.ylabel("x2")
plt.legend()
plt.show()

  
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

# LDA(Linear Discriminant Analysis)를 통해 새로운 데이터가 어느 클래스에 속할 확률이 높은지 확인
# LDA = 두 클래스(또는 여러 클래스)를 가장 잘 구분할 수 있는 선형 경계선을 찾아 데이터를 그 선 위에 투영해서 분류하는 알고리즘
model = LinearDiscriminantAnalysis().fit(X, y) # 학습
p = model.predict_proba([[-0.2, -0.1]]) # 새 데이터 확률 예측
print(model.classes_)
# 결과 -> y = 0일 확률 0.68997448, y = 1일 확률 0.31002552
print(p)


# 결정 경계 시각화
# -4~4까지 200개 점 / -3~3까지 200개 점 생성하고, 두 벡터를 통해 좌표 평면 전체의 격자점 생
x1, x2 = np.meshgrid(np.linspace(-4, 4, 200), np.linspace(-3, 3, 200))
# .ravel() -> 2D -> 1D flatten
# .flatten()은 원본 벡터 복사 후 평탄화, .ravel()은 원본 공유하므로 후자가 더 빠름
# np.c_[] -> 1D 배열 두 개를 옆으로 붙여 N * 2 형태로 만듦.
grid = np.c_[x1.ravel(), x2.ravel()]
# 각 점에 대해 [P(y=0), P(y=1)] 계산하고, y=1일 확률만 가져옴.
probs = model.predict_proba(grid)[:, 1].reshape(x1.shape)

# contourf() 확률값을 색으로 채우는 함수
# 0~0.5 → y=0 쪽 (검정 영역), 0.5~1 → y=1 쪽 (흰색 영역)
plt.contourf(x1, x2, probs, levels=[0, 0.5, 1], alpha=0.2, colors=['black', 'white'])
# 결정 경계선 표시 (P(y=0|x) = P(y=1|x) = 0.5, 둘의 확률이 같은 지점)
plt.contour(x1, x2, probs, levels=[0.5], colors='red', linewidths=2)

# 기존 데이터 시각화
plt.scatter(X[:3, 0], X[:3, 1], c="k", s=50, edgecolor='k', label="y=0")
plt.scatter(X[3:, 0], X[3:, 1], c="w", s=50, edgecolor='k', label="y=1")

# 테스트 포인트 시각화
plt.scatter(-0.2, -0.1, c='r', s=100, marker='x', edgecolor='k', linewidth=2)
plt.xlabel("x1")
plt.ylabel("x2")
plt.legend()
plt.title("LDA Decision Boundary & Test Point")
plt.show()

확률적 판별 모형

• 조건부 확률 P(y=1|x)이 x에 대해 함수 f(x)로 표현될 수 있다 가정하고, 그 함수를 직접 찾아내는 방법
• 각 클래스가 데이터를 어떻게 만들어내는지를 모델링함. (주어진 x에서 y가 될 확률은 함수 f(x)로 표현된다고 가정, 이 함수는 시그모이드나 소프트맥스 함수로 표현됨.)
• P(y = k | x) = f(x), 0 <= f(x) < 1
• (ex) Logistic Regression 등

from sklearn.linear_model import LogisticRegression

model = LogisticRegression().fit(X, y) # 로지스틱 회귀 모델 학습
p = model.predict_proba([[-0.2, -0.1]]) # 테스트 데이터 확률 예측
print(model.classes_)
print(p) # [[0.55811895 0.44188105]], y=0일 확률이 더 높음
  
# 시각화
x1, x2 = np.meshgrid(np.linspace(-4, 4, 200),
                     np.linspace(-3, 3, 200))
grid = np.c_[x1.ravel(), x2.ravel()]

# 각 좌표에 대해 y=1 확률 계산
probs = model.predict_proba(grid)[:, 1].reshape(x1.shape)

# 결정 경계선 표시
plt.contourf(x1, x2, probs, levels=[0, 0.5, 1],
             alpha=0.2, colors=['black', 'white'])
plt.contour(x1, x2, probs, levels=[0.5],
            colors='red', linewidths=2)

# 원래 데이터
plt.scatter(X[:3, 0], X[:3, 1], c="k", s=50, edgecolor='k', label="y=0")
plt.scatter(X[3:, 0], X[3:, 1], c="w", s=50, edgecolor='k', label="y=1")

# 테스트 포인트 (빨간 X)
plt.scatter(-0.2, -0.1, c='r', s=100, marker='x', edgecolor='k', linewidth=2)

plt.xlabel("x1")
plt.ylabel("x2")
plt.legend()
plt.title("Logistic Regression Decision Boundary & Test Point")
plt.show()

** 확률적 생성 모형은 각 클래스가 데이터를 어떻게 만들어내는지를 모델링하고, 확률적 판별 모형은 각 클래스 사이를 어떻게 구분할지를 학습한다.

2. 판별 함수 모형

• 주어진 데이터를 카테고리에 따라 서로 다른 영역으로 나누는 경계면(decision boundary)을 찾아낸 다음 이 경계면으로부터 주어진 데이터가 어느 위치에 있는지를 계산하는 판별함수(discriminant function)를 이용하는 모형
• 경계면으로부터의 거리를 계산하는 판별함수(discriminant function) f(x)로 경계면을 정의함. (확률을 보지 않고, 경계선의 위치를 직접 계산하는 모델. 예를 들어 퍼셉트론 -> f(x) > 0이면 1, 아니면 0 / 확률 계산 없음, 단순히 한쪽 or 다른 한쪽)
• 클래스를 구분하는 경계선을 찾는 것
• (ex) Perceptron, SVM, Neural Network 등
  • SVM : 두 클래스 사이 마진을 두고, 그 마진이 최대가 되도록 경계선을 그음

import numpy as np
import matplotlib.pyplot as plt

x_train = np.array([[170, 80], [160, 70], [180, 80], [160, 90], [150, 80]])
y_train = np.array([0., 0., 0., 1., 1.])

plt.plot(x_train[:3, 0], x_train[:3, 1], 'bo') # [:3] - y = 0
plt.plot(x_train[3:, 0], x_train[3:, 1], 'ro') # [3:] - y = 1
plt.grid()
plt.show()

W = np.random.normal(size = 1 + x_train.shape[1]) # 초기 가중치 설정, 1 -> bias // W = [b, w1, w2]
print("initial weights : ", W)

# H(x) = wx + b
def H(x):
  return np.dot(x, W[1:]) + W[0]

# H(x)가 0 이상이면 클래스 1, 미만이면 클래스 0
def predict(X):
  return np.where(H(X) >= 0.0, 1, 0)

epochs = 100 # 에폭
learning_rate = 0.01 # 학습률

for i in range(epochs):
  cost = 0 # 해당 에폭에서 수정된 데이터 개수
  for xi, target in zip(x_train, y_train):
    update = learning_rate * (predict(xi) - target) # 예측값과 실제값 차이 계산
    # w, b 업데이트
    # 예측값과 정답이 다르면 update 값이 0이 아님 -> 가중치 수정
    # 같으면 update = 0, 수정하지 않음
    W[1:] -= update * xi
    W[0] -= update
    cost += int(update != 0.0)

  if i % 10 == 0:
    print('Epoch ({:5d}/{:5d}) cost : {:5d}, W : {}, b : {}'.format(i, epochs, cost, W[1:], W[0]))

print("W : {}".format(W)) # 가중치
print("result : ")
print(predict(x_train)) # 결과 

print(predict([172, 73])) # 정상 (0)
print(predict([150, 80])) # 비만 (1)