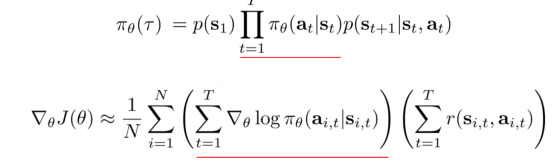REINFORCE

 REINFORCE는 정책(행동 확률 분포)을 직접 학습하는 강화학습 알고리즘으로, 보상에 따라 행동 확률을 조정하며 최적 정책을 찾아가는 방법이다. 이때, 상태로부터 행동 확률을 도출하는 파라미터 기반의 정책을 학습하며, 에이전트는 환경 속에서 취할 행동을 이 정책으로부터 학습한다. 다시 말해, REINFORCE에선 정책을 파라미터를 가진 함수로 표현하고, 이 파라미터를 보상에 따라 업데이트하면서 최적 정책을 찾아간다.

 REINFORCE의 핵심 개념은, 좋은 결과를 초래했던 행동이 더 높은 확률로 선택되도록 에이전트를 학습시켜야 한다는 것이며, 이 과정에서 학습이 성공적이라면 주어진 환경에서 정책이 만들어 내는 행동 확률 분포는 많은 반복 학습을 통해 결과를 도출하는 분포로 이동하게 된다.

 이 행동 확률은 정책 경사(policy gradient)를 따라 변하기에, REINFORCE 알고리즘은 정책 경사 알고리즘이라고도 한다.

 또한, REINFORCE 알고리즘은 파라미터 업데이트 방정식이 현재의 정책에 따라 결정되므로 활성 정책 알고리즘이며, 정책 경사가 과거의 어떤 정책이 아닌 현재의 정책에 의해 생성된 행동 확률에 직접적으로 영향을 받고, 이득 또한 정책 $\pi_\theta$로부터 생성되어야 한다. (그렇지 않으면 행동 확률이 정책이 생성하지 않은 이득에 근거하여 조정되기 때문이다.)

 이러한 REINFORCE 알고리즘은 다음과 같은 세 가지 필수 요소를 지닌다.

1. 파라미터로 표현된 정책
2. 최대한 달성하고자 하는 목적
3. 정책 파라미터를 업데이트 하는 방법

정책

 정책은 상태와 행동 확률을 매핑하는 함수이다. REINFORCE에서의 정책 $\pi_\theta$는 정책망(policy network)이라고도 불리며, 할인된 보상의 누적값을 최대로 만드는 정책(좋은 정책)을 만들기 위해 함수 근사를 활용한다.

 이때, 정책의 파라미터 값에 따라 하나의 신경망으로 각기 다른 행동 확률을 도출할 수도 있다. 따라서 REINFORCE에서의 좋은 정책을 학습하는 방법은 좋은 $\theta$ 값을 찾는 것이다.

 좋은 정책을 학습하기 위해 경사 상승(gradient ascent)를 적용하여 정책을 향상시킬 수 있는데, 이는 목적 함수인 $J(\pi_θ)$를 최대화하는 방식으로 진행된다. 이를 통해 목적 함수가 커지는 방향으로 파라미터 학습을 진행하게 되므로 보상이 큰 행동은 더 자주, 적은 행동은 덜 나오도록 업데이트된다.

$θ ← θ + α∇_θ​J(\pi_θ)$ # 보상이 커지는 방향으로 파라미터 업데이트 (클수록 좋은 정책)

목적 함수

 REINFORCE 알고리즘에서 에이전트가 최대로 달성하고자 하는 목적(에이전트의 목표)은 에이전트가 생성하는 모든 완전한 궤적에 대한 이득의 기댓값으로, 정책으로부터 추출된 수많은 궤적에 대해 기댓값이 계산된다. 또한, 추출된 표본의 개수가 많을수록 기댓값은 참 값에 가까이 접근한다. (다시 말해, 표본의 개수가 많을 수록 기댓값 추정이 정확해진다는 것이다.)

• 궤적 (τ) : 환경에서 처음부터 끝까지 에이전트가 경험한 상태–행동–보상의 시퀀스
• 궤적의 이득 (return) : 한 궤적에서 얻은 보상들의 할인된 합
• 목적 함수 : 정책 $\pi_\theta$가 만들어내는 모든 궤적에 대해 이득 𝑅(𝜏)의 기댓값을 취한 것
  $J(\pi_θ) = E_{τ∼π_θ} [R(τ)]$

정책 경사

 정책 경사는 알고리즘은 $J(\pi_θ) = E_{τ∼π_θ} [R(τ)]$를 최대화하는 θ를 해결하는 문제로 정의할 수 있다. 목적을 최대로 달성하기 위해 정책 파라미터 θ에 대한 경사 상승을 수행하며, 경사는 가장 가파르게 상승하는 방향으로 계산된다. 파라미터 업데이트 식은 앞에서도 봤듯 $θ ← θ + α∇_θ​J(\pi_θ)$이다.

 이때, α는 학습률을 나타내는 스칼라값으로 파라미터 업데이트의 크기를 조절하고, $∇_θ​J(\pi_θ)$는 정책 경사를 나타내며, 다음과 같이 표현될 수 있다.

 이때, $\pi_\theta(a_t|s_t)$는 에이전트가 시간 단계 t에서 취하는 행동의 확률을 의미하며, 행동은 정책으로부터 추출되므로 $a_t$는 정책 $\pi_\theta(s_t)$가 정의하는 확률 분포 내에서 샘플링된다.

 정책 경사는 정책으로부터 생성된 행동 확률을 변화시키는 매커니즘으로, 이득 $R(τ) > 0$이면, 행동 확률은 증가하고, 이득 $R(τ) < 0$이면 행동 확률은 감소한다. 따라서 많은 업데이트 과정을 통해 정책은 높은 $R(τ)$ 값을 도출하는 행동을 생성하도록 학습한다.

참고로, 그냥 확률을 사용하지 않고 로그 확률을 사용하는 이유는, 각 state, action에 대한 확률을 계속 곱해나가다 보면, (확률은 항상 [0, 1] 사이 범위이므로) 역전파 시 기울기 소실이나 폭발 문제가 발생할 수 있는데, 이를 방지하기 위함이다. 또한, 로그 계산 시에는 곱셈이 덧셈으로 바뀌므로 수치적으로도 안정성을 확보할 수 있다.

몬테카를로 표본 추출

 REINFORCE 알고리즘은 몬테카를로 표본추출을 이용해 수치적으로 정책 경사를 추정한다. 이때, 몬테카를로 표본 추출은 어떤 값의 기댓값을 정확히 계산하기 어려울 때, 무작위 샘플링을 통해 근사하는 기법을 의미한다.

 REINFORCE의 목적 함수는 궤적 전체에 대한 이득의 기댓값

 인데, 이 기댓값을 직접 계산하기는 어려우므로, 대신 정책으로부터 여러 번 에피소드를 실행해 보상을 얻고, 그것의 평균을 내 기댓값에 근사한다. 이를 몬테카를로 표본 추출이라고 하며, 앞에서 표본의 수가 많아질수록 추정치가 실제 참 값(기댓값)에 가까워진다는 것은 이러한 이유 때문이다.

향상된 REINFORCE

 몬테카를로 표본추출로 생성된 하나의 궤적을 이용해 경사를 추정하는 REINFORCE 알고리즘은 정책 경사에 대해 편차 없는 추정값을 내지만, 추정값이 큰 분산을 갖는다는 문제가 있다.

 이러한 문제가 발생하는 이유는 다음과 같다.

1. 행동이 확률분포로부터 추출됐기에 어느 정도 무작위성을 갖는다
2. 시작 상태가 에피소드마다 다를 수 있다
3. 환경의 전이 함수가 확률론적일 수 있다.

 이러한 문제를 해결하기 위한 방법 중 하나로는, 행동에 영향을 받지 않는 적절한 기준값을 이득에서 빼 이득을 조절하는 방법이 있으며, 보상에서 기준 값을 빼줌으로써 gradient 기댓값은 동일하게 유지하되, 분산을 줄일 수 있다.

 기준값으로 삼을 수 있는 것 중에는 가치 함수 $V^\pi$가 있고, 또다른 것에는 궤적에 대한 평균 이득을 기준값으로 하는 것이 있다. 즉, 아래의 식을 기준값으로 삼는 것이다. 이를 통해 각 궤적마다 이득의 분포가 0을 중심으로 형성되게 할 수 있다. (centering 느낌, 평균보다 크면 +, 작으면 - -> 학습 안정 효과)