Index
Summary
- Hash-based indexes: best for equality searchs, cannot support range searches.
- Static Hashing can lead to overflow chains.
- Extendible Hashing avoids overflow pages by splitting a full bucket a new data entry is added to it.
- Directory keeps track of buckets, doubles periodically.
- Linear Hashing avoids overflow pages by splitting buckets in round-robin, without using a directory.
Linear Hashing은 directory가 왜 필요없는지 이해해야하고, directory에 I/O가 쓰이지 않는다는 것을 알아야한다. -> overflow page가 sequentially하게 저장되니까?
Summary (Contd.)
- For hash-based indexes, a skewed data distribution is one in which hash values of data entries are not uniformly distributed!
- Both EH and LH degrade in performance when distribution is skewed.
- In this course, we assume 1.2 pages for each bucket of EH and LH.과제나 시험에서도 hash index의 I/O는 1.2로 계산해라

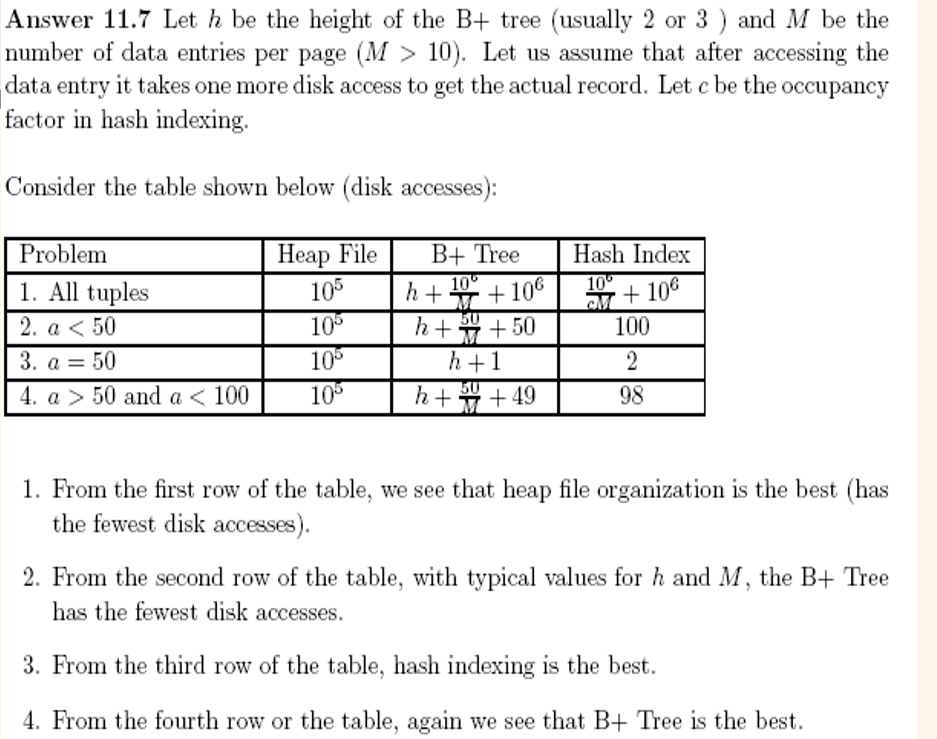
각 페이지에 10개의 data record가 들어가있다고 말했으니, data entries는 더 많이 들어갈 수 있다. 따라서 (M > 10)
총 1 million records가 있고, 한 page는 10 record를 저장하니 10^5 개의 페이지가 있다.
- All tuples - B+ Tree : B+ 트리는 일단 h만큼 data entries 젤 왼쪽 끝으로 내려가야한다. 그 다음 오른쪽으로 연결되어있으니 data entries들을 이동한다. (10^6개의 record가 있고 page에 M개의 record가 있으니 data entries는 10^6 / M개가 있다). 각각의 record에 대해 조회해야하니 또 10^6만큼 I/O 발생한다.
- All tuples - Hash Index: data entries page에 c만큼 차있다. 따라서 10^6 / cM만큼 읽어야한다. 그다음 각각 record를 읽어야하니 10^6만큼 I/O가 발생한다.
- a < 50 - Heap File: Heap은 어떤 순서가 없으므로 전부 다 읽어야한다.
- a < 50 - B+ Tree:
처음 h만큼 내려가고나서, 왼쪽으로 가면된다. 각 data entries에 대해 record를 읽어야하니 50을 더한다.
- a < 50 - Hash Index:
a < 50은 50개의 query로 생각할 수 있다. a=1, a=2, .... 각각의 query에 대해 data entry에 한번 접근하고, data record에 한번 접근한다. 따라서 100.
따라서 range query 일때는 B+ Tree가 제일 낫다.
- a = 50 - B+ Tree:
높이만큼 내려가고, data record를 읽어오면된다.
- a = 50
hash이므로 data entry 한번, record 한번해서 총 2번.
- a > 50 and a < 100:
2번과 비슷하다.
여기서 1.2 I/O를 쓰지 않은 이유는 100퍼센트 full이 아니기 때문이다. 1.2를 쓰는 이유는 overflow pages가 있을 때 간단히 계산하기 위해서이다
만약 clustered 였다면 range qurty에서, 밑에 data record들이 다 정렬되어있을 것이고, 그럼 data entry하나만 읽고 data record로 간다음 왼쪽으로 가면된다.?
extendible hash에서 directory가 쓰이나, 파일이 너무 크지 않는이상, 메모리에 있으면 count가 필요없고 메모리에 없어도 1밖에 차이가 안난다.

이것은 unclustered index이다. record(여기서는 book page)도 search key에 따라 정렬되어야한다.
이것은 alternaitve 3이다. 한 search key에 여러개의 rid가 붙어 있는 것도 있으니 list of rids이다.
