Day 1
Midterm1
Day 2
The Dual Simplex Method
As we saw in out discussion of the strong duality theorem, one can actually apply the simplex methodto the dual problem without every writing downt he dual or its dictionaries. Instead, the so-called dual simplex method is seen simply as a new way of picking the entering and leaving variables in a sequence of primal dictionaries.

Example

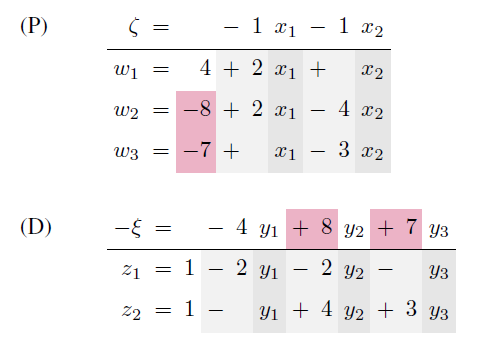
As before, we have recorded the negative of the dual objective function, since we prefer to maximize the objective function appearing in a dictionary. More importantly, note that the dual dictionary is feasible, whereas the primal is not. This suggests that it would be sensible to apply the simplex method to the dual. Let us do so, but as we go we keep track of the analogous pivots applied to the primal dictionary.
For example, the entering variable in the initial dual dictionary is y2, and the leaving variable then is z1. Since w2 is complementary to y2 and x1 is complementary to z1, we will use w2 and x1 as the entering/leaving variables in the primal dictionary. Of course, since w2 is basic and x1 is nonbasic, w2 must be the leaving variable and x1 the entering variable—i.e., the reverse of what we have for the complementary variables in the dual dictionary.
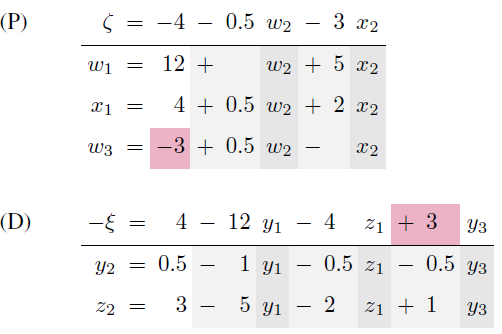
Continuing to work on the dual, we now see that y3 is the entering variable and y2 leaves. Hence, for the primal we use w3 and w2 as the leaving and entering variable, respectively.
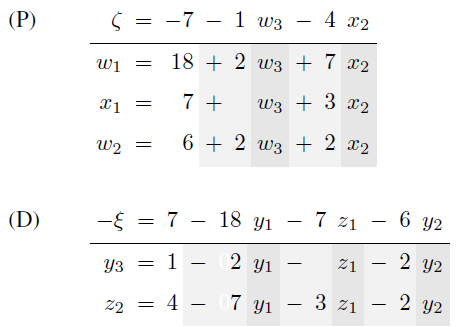
Now we notice that both dictionaries are optimal.
Of course, in each of the above dictionaries, the table of numbers in each dual dictionary is the negative transpose of the corresponding primal table. Therefore, we never need to write the dual dictionary; the dual simplex method can be entirely described in terms of the primal dictionaries. Indeed, first we note that the dictionary must be dual feasible. This means that all the coefficients of the nonbasic variables in the primal objective function must be nonpositive. Given this, we proceed as follows. First we select the leaving variable by picking that basic variable whose constant term in the dictionary is the most negative (if there are none, then the current dictionary is optimal). Then we pick the entering variable by scanning across this row of the dictionary and comparing ratios of the coefficients in this row to the corresponding coefficients in the objective row, looking for the largest negated ratio just as we did in the primal simplex method. Once the entering and leaving variable are identified, we pivot to the next dictionary and continue from there.
Day 2 - Lecture Note





leaving variable을 정할 때는, constrain의 우항에 가장 -값이 큰 constant를 가지고 있는 것을 고른다. dual을 만들때 negative transpose 하는 것을 생각하면 왜 가장 - 값이 큰 constant를 가진 contraint를 고르는지 이해하기 쉽다.
entering variable을 정할때는 세로 column으로 비교하여, objective func의 coeff에는 -를 붙이고, leaving var의 row와 비율을 따져서 가장 큰 것을 고른다. 여기서 leaving var는 w2이고 x1의 비율은 (--1)/2이므로 1/2이고 , x2의 비율은 (--1)/-4이므로 -1/4이다. x1의 비율이 가장 크므로 entering variable은 x1이다.
쉽게 말해 먼저 contraint 즉 row가 정해지고, 그 row의 coeff와 그대로 쭉 올려서 objective func의 coeff와 하나씩 비교하는 것이다.


Day 3
Lecture Note
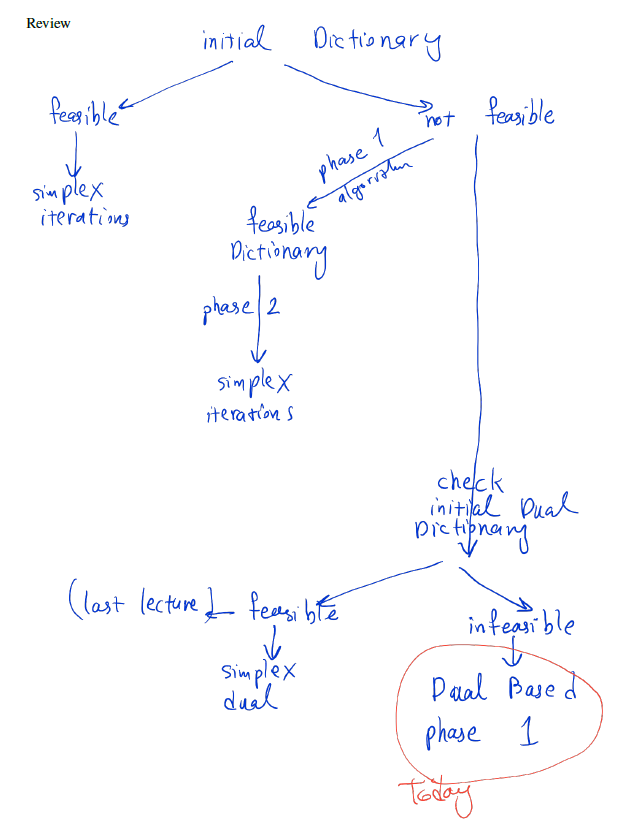
The Dual-based Phase 1 Algorithm






The Daul of a Problem in General Form



Rules for forming the dual


