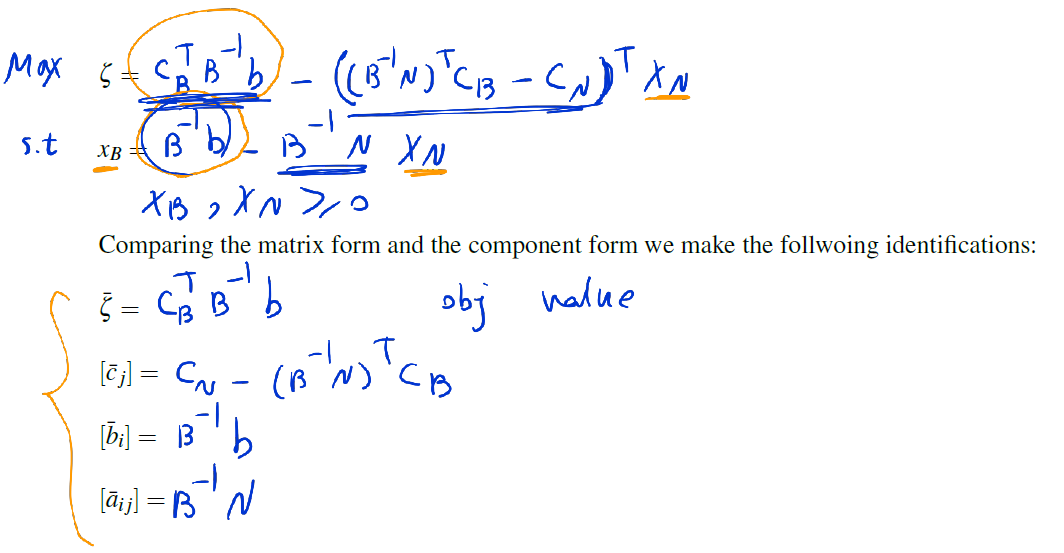Day 1
Lecture Note
Resource Allocation Problem
Let us return to the production facility problem in chapter 1. The problem involves a production facility that can take a variety of raw materials (enumerated i=1,...,m) and turn them into a variety of final products (enumerated j=1,...,n).

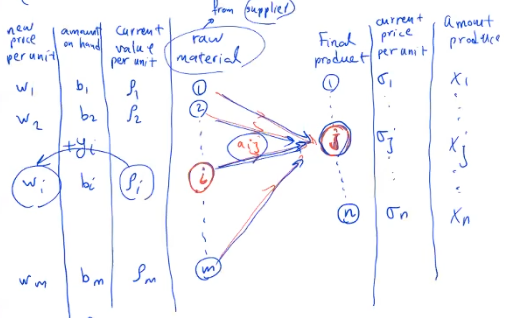
The following equation holds whenever the market is in equilibrium.

current price per unit of final product = current value per unit * raw material
In real world some perturbations move the equilibrium to new levels. For example, if the production process is improved such that some a_ij's are reduced, then there is a windfall profit for each unit of product j. The profit is given by

Once the suppliers get wind of the profit being made, they increase the price of the raw materials. There is a time lag (assume one month) and during this time fortunes are made.
Variables
w_i : The new price for the raw material i at the end of the time lag (here is one month).
y_i: Increase in the price of raw material i. (wi = ri+yi)
x_j: Production manager decides to produce xj units of product j.
w_i & y_i : decided by supplier
x_j : decided by production manager
Therefore,

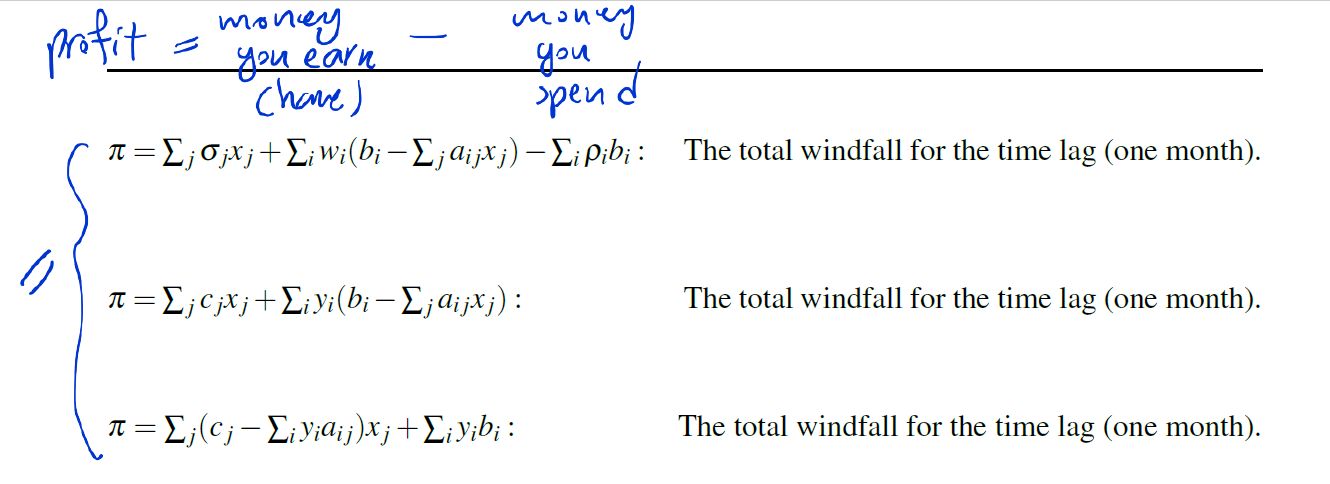

The production manager's aim is to chose x_j that maximize the windfall.
The supplier's aim is to choose prices w_i that minimize the windfall.
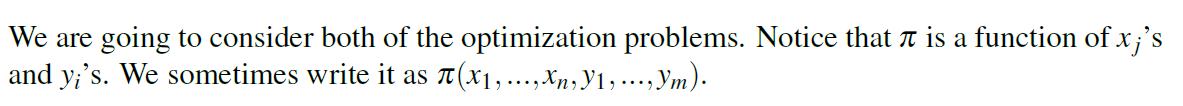
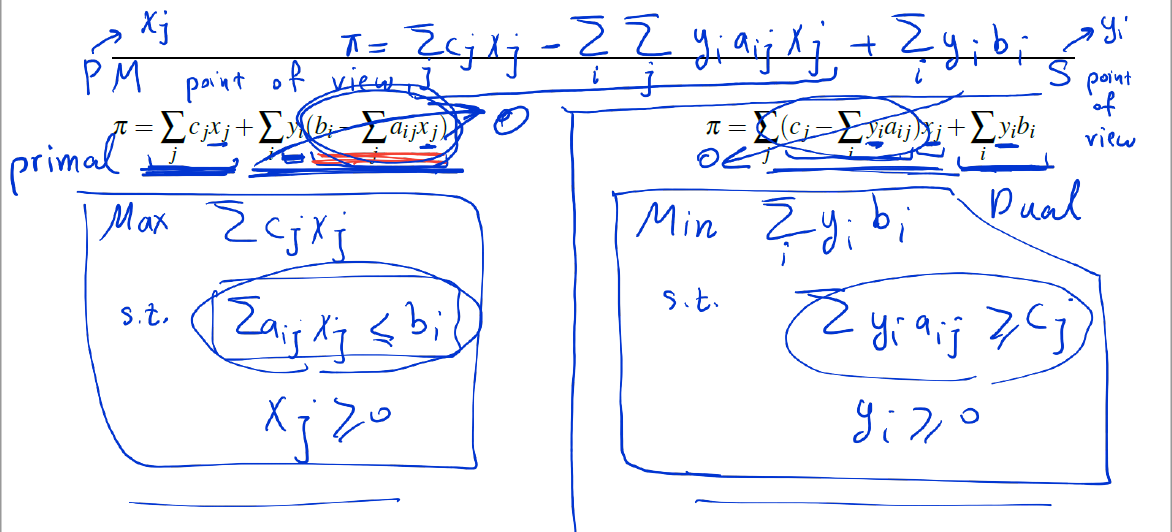
Production Manager's Point of view

supplier는 파이를 minimize 하려고한다.
Supplier's Point of View

production manager는 파이를 maximization하려한다.
Day 2
Lecture Note
Lagrangian Duality
The analysis of the proceeding section is an exampleof a general technique that forms the foundation of a subject called Lagrangian duality, which we shall briefly describe.
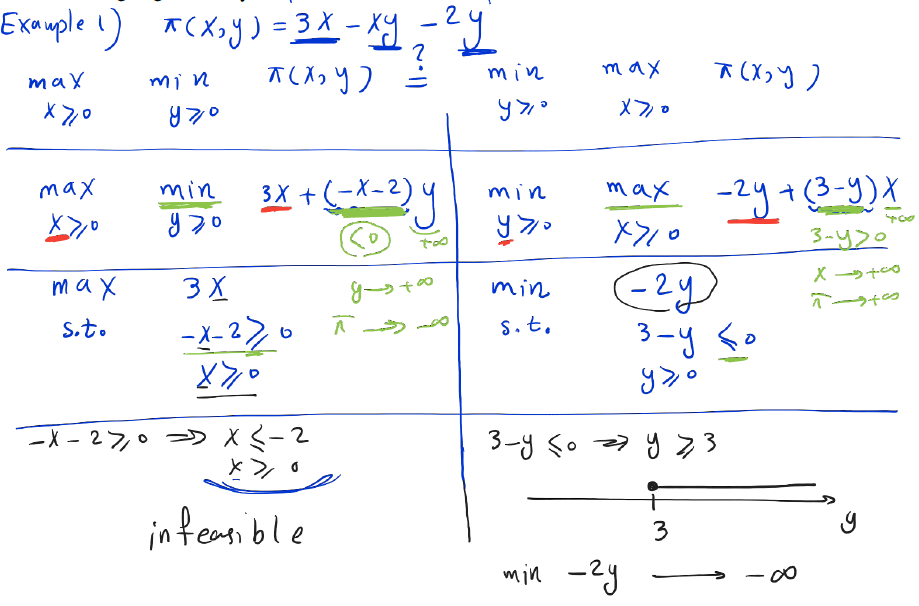
Let us start by summarizing what we did. The analysis revloveed about the function


We also showed that the inner optimization could in both cases be explicitly. The max-min problem reduce tot he primal linear programming problem, and the min-max problem reduced to the dual linear programming problem.

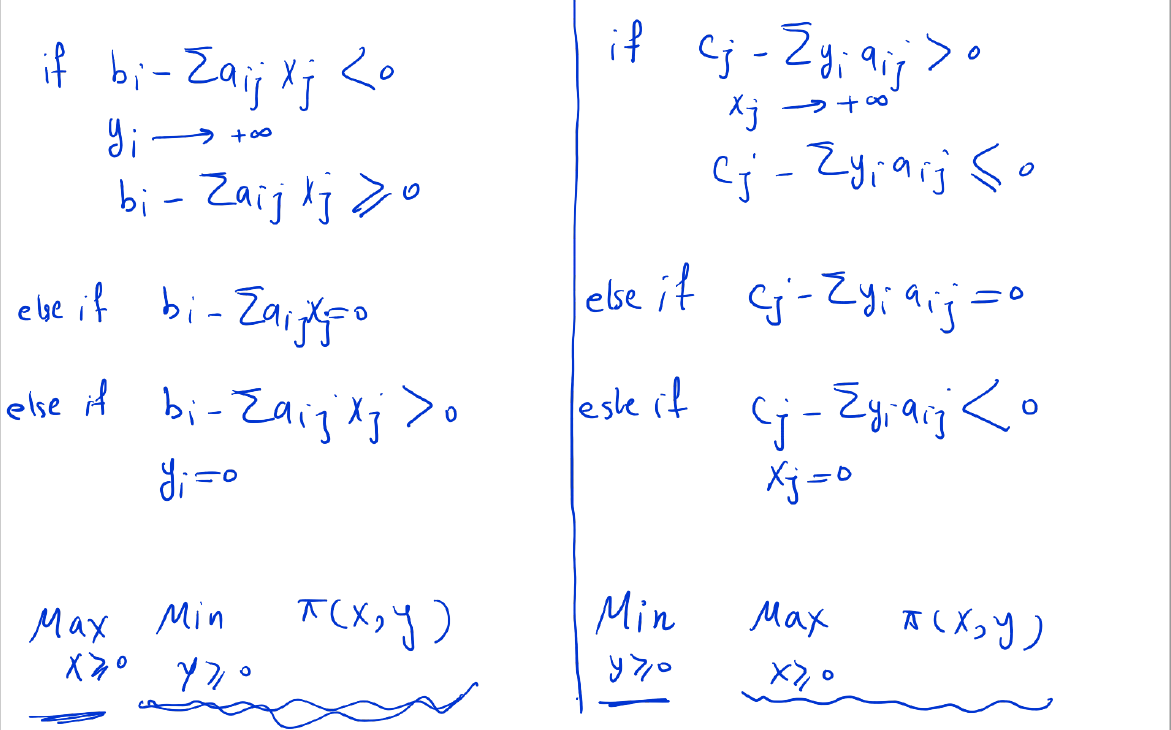


Day 3
Lecture Note
The Simplex Method in Matrix Notation
In this chapter we use matrix notation to present linear programming problems. At the same time, we will emphasize the close relations between the primal and dual problems.
Linear Programming Problem Matrix Notation
We begin our discussion with the standard form linear programming problem:

In the past, we have denoted slack variables by w_i's. Here, we introduce slack variables as follows:
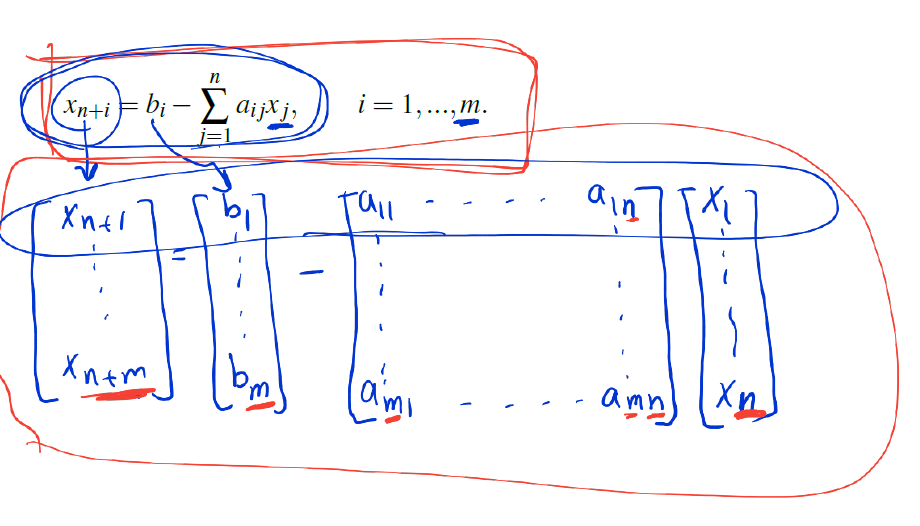
With these slack variables, we now wirte our problem in matrix form:

In total, we have n + m variables.
m basic variables denoted by B and n non-basic variables denoted by N.
Let B denote an m x m matrix whose columns are the m columns of A that are associated with the basic variables.
Let N denote an m x n matrix whose columns are the n columns of A that are associated with the nonbasic variables.


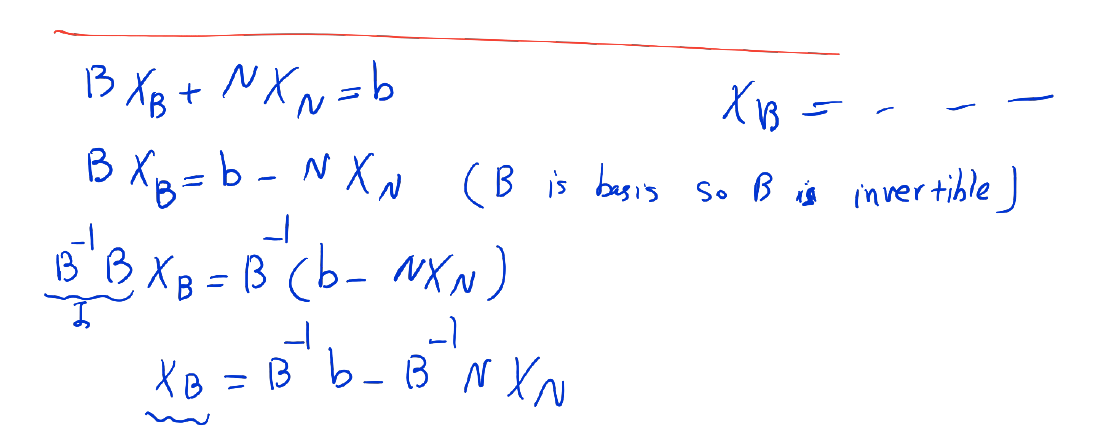
The Dictionary Matrix Notation