백준 - 동전 1

내 풀이

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

public class baekjoon_2293 {

    static int n, k;
    static int[] dp;
    static int[] coins;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] inputs = br.readLine().split(" ");
        n = Integer.parseInt(inputs[0]);
        k = Integer.parseInt(inputs[1]);

        dp = new int[k+1];
        coins = new int[n];

        for (int i = 0; i < n; i++) {
            int coin = Integer.parseInt(br.readLine());
            coins[i] = coin;
        }

        //n가지 종류로 k원을 만드는 방법은
        // 1) n-1가지로 k 만드는 경우의 수
        // 2) n가지 동전으로 k - coins[n] 경우의 수
        dp[0] = 1; //0원을 만드는 방법은 아무것도 안내는 방법 1가지다
        for (int i = 0; i < n; i++) {
            for (int j = 0; j <= k; j++) {
                if (j - coins[i] >= 0) {
                    dp[j] += dp[j - coins[i]];
                }
            }
        }
        System.out.println(dp[k]);

    }
}

예전에 풀어봤지만 그때도 풀이를 찾아보고 풀었거나 기억에 의존해 풀었기에 이번 기회에 정리를 한다.

N가지 종류의 동전으로 K원을 만드는 방법은 두 가지다.
1) N번째 동전 없이 N-1가지의 동전으로 K를 만들기
2) N가지 동전으로 K - coins[n]의 경우의 수 (K - coins[n]을 만드는 방법에 coins[n]만 더하면 K를 만들 수 있다)

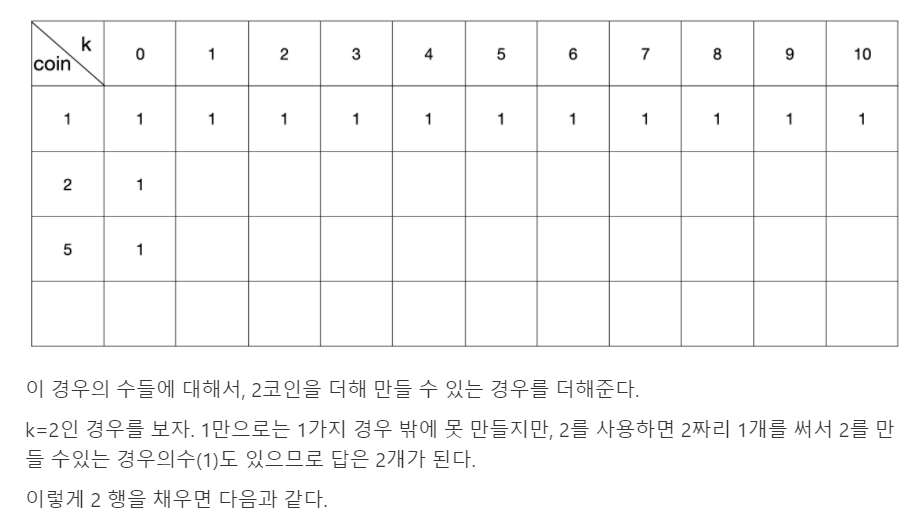
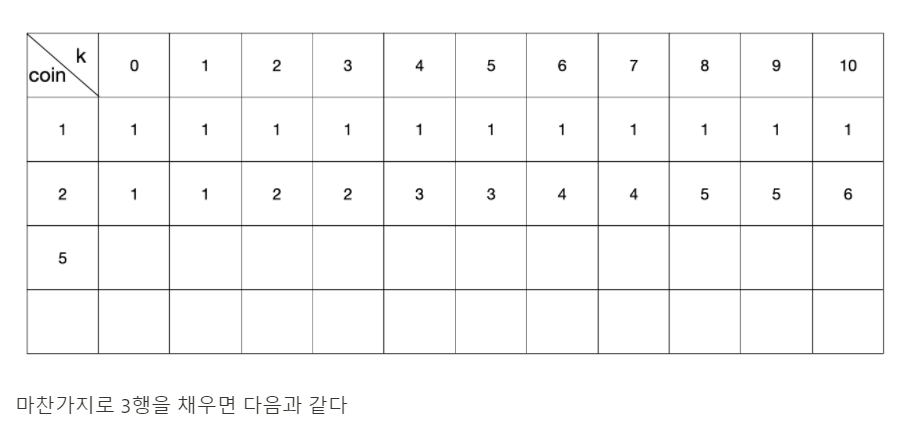
따라서 원래는 아래와 같이 2차원 테이블이 형성돼야 한다.

하지만 결국 테이블에서 dp[i][j]를 채우는 방법은 dp[i-1][j] (i번째 동전 없이 j원 만들기) + dp[i]j - coins[i]] (모든 동전을 써서 j - coins[i]원 만들기) 이다. 따라서 열 방향으로 누적되며 내려오기 때문에 행을 재활용 할 수 있는 것이다.

2022-07-11

# n가지 종류, 가치의 합 k
n, k = map(int, input().split())

dp = [0] * (k + 1)
coins = [int(input()) for _ in range(n)]
dp[0] = 1

for i in range(n):
    for j in range(k+1):
        if j - coins[i] >= 0:
            dp[j] += dp[j - coins[i]]

print(dp)
print(dp[k])

우선 정확한 뒤의 구동 원리를 이해하려면 위에 테이블을 보고 이해하면 된다.

n가지 종류로 k원을 만드는 방법은
1) n-1가지로 k 만드는 경우의 수
2) n가지 동전으로 k - coins[n] 경우의 수

바깥의 for 문에서 n만큼 반복하니 테이블에서 행을 따라 내려온다. 그리고 열을 차례대로 반복하는 것이다.
그래서 2차원 배열 없이 누적을 통해서 2차원 배열을 도는 효과를 낼 수 있다.

처음에는 왜 for문 바깥에 n이 아닌 k+1을 반복하면 안될까 생각해봤는데 그러면 3원을 만들 때 (1,2), (2,1) 같이 동전 중복을 다 카운팅할 것 같다.