순차적 자료구조: Linked List - Singly, Doubly, Circular

인마헷·2023년 11월 16일
자료구조
0

자료구조

목록 보기
3/4
post-thumbnail

정말정말 양도 많고 할 것도 많은 링크드 리스트.

데이터가 순차적으로 저장되어있지 않다.

링크드 리스트(Linked list)

근데 링크드 리스트는 순차적 자료구조에 해당한다.

왜 순차적 자료구조인가? 다음 데이터가 어디에 저장되어있는지 본인이 가리키고 있거든. 그래서 순차접근이 필요한 자료 구조이다.

데이터를 담은 구조를 노드라고 하고 그 노드와 다음 노드와의 연결을 링크라고 한다. 연결된 리스트 중 가장 앞에 있는 노드는 헤드 노드라고 한다.

놀라운 점은(별로 놀랍지 않을 수도 있지만) 배열에서 느꼈던 인덱스의 강력함을 여기서는 경험할 수 없다. 만약 인덱스 10번에 있는 값을 알고 싶다? 헤드 노드부터 해서 쭉 링크를 타고타고 따라가야 인덱스 2에 있는 값을 알아낼 수 있다.

그렇다면, 왜 쓰냐? 대표적인 장점이 있는데 앞서 본 배열에서는 중간에 삽입을 하고 싶으면 그 위치 이후에 있는 친구들을 한 칸씩 다 미뤄줘야 하는 이동 연산을 해야했다. 그럼 최악의 경우, 가장 첫 번째에 값을 추가하고 싶어, 그럼 기존 배열의 길이인 N시간 만큼의 이동 연산이 필요하게 된다.

근데 링크드 리스트의 경우는 삽입 연산이 상수 시간에 가능하다. 각 노드는 자기 다음에 올 노드를 가리키고 있다. 그래서 이 링크가 가리키는 부분만 바꿔주면 되는데 이 링크 변경은 상수 시간에 가능하기 때문에 링크드 리스트는 삽입에 O(1)이다. 마찬가지로 삭제도 링크 끊어주면 되니까 상수 시간에 가능하다.

이 링크드 리스트도 두 가지 종류가 있는데 링크가 한쪽으로만 가냐, 양끝에서 오냐로 나뉜다.

1. Singly Linked List(일방향 연결리스트)

앞서 본 스택과 큐처럼 클래스를 선언해서 구조를 보고자 한다.

먼저, Node class를 만들어보자. 각 노드는 키와 다음 아이를 가리킬 링크가 필요하다. 필요에 따라서는 value도 추가할 수 있는데 일단, 최소화한 구조에서 시작하도록 하겠다. 

class Node:
	def __init__(self, key=None):
		self.key = key
		self.next= None
	
	# 노드의 키값을 그냥 프린트 하고 싶으면 경우
	# print(v.key) -> 이렇게 해야 되는걸 
	# print(v) -> 이렇게 하고 싶엉
	def __str__(self):
		return str(self.key)

a = Node(3)
b = Node(9)
c = Node(-1)

a.next = b
b.next = c

# 귀찮잖아. 헤드 노드만 알고 싶어. 그래서 또다른 클래스를 만들어
# 그 헤드 노드를 가리키는 클래스인거야. 
# 결국 한방향 연결 리스트의 객체임. 

class SinglyLinkedList:
	def __init__(self):
		self.head = None
		self.size = 0

	# insert, remove method는 이하 코드에서. 
	
	def __len__(self):
		return self.size

자료구조 연산 중 삽입과 삭제를 살펴보자

insert, remove

삽입과 삭제는 각각 push와 pop 연산인데, 링크드 리스트에는 헤드와 테일(tail),링크 등이 연관되어있기 때문에 push, pop이 이뤄지기 때문에 각각을 따로 살펴봐야 한다.

즉, pushFront와 pushBack, popFront, popBack을 개별적으로 살펴보면 아래와 같다. 

class Node:
    def __init__(self, key=None):
        self.key = key
        self.next = None

class SinglyLinkedList:
    def __init__(self):
        self.head = None
        self.size = 0

    def pushFront(self, key):
        newNode = Node(key)
        newNode.next = self.head
        self.head = newNode
        self.size += 1

    def pushBack(self, key):
        v = Node(key)
        if len(self) == 0:
            self.head = v
        else: # 우리가 테일은 모르잖아. 헤드부터 찾아가야 하는거야.
            tail = self.head
            while tail.next != None:
                tail = tail.next # 노드 이동을 표현한 거. 
            tail.next = v
        self.size += 1

	# 지울 때는 일단 리스트가 비어있는지 확인해야 함.
    def popFront(self):
        if len(self) == 0:
            return None
        else:
            x = self.head
            key = x.key
            self.head = x.next
            self.size -= 1
            del x # 메모리에서 릴리즈
            return key

    def popBack(self):
        if len(self) == 0:
            return None
        else:
            prev, tail = None, self.head
            while tail.next != None:
                prev = tail
                tail = tail.next

						# 노드가 하나인 경우
            if len(self) == 1:
                self.head = None
            else:
                prev.next = None
            key = tail.key
            del tail
            self.size -= 1
            return key

    def __len__(self):
        return self.size

앞에서 삽입과 삭제하는 연산인 pushFront, popFront은 링크 변경 연산(+삭제같은 경우는 메모리 삭제 연산 등)만 진행하면 되기에 O(1)의 시간이 걸리는데, 테일을 쫓아가봐야 하는 pushBack, popBack의 경우는 링크드 리스트의 노드 개수 만큼의 시간이 소요된다. 코드에서 while로 tail을 찾아가는 과정이 그러하다.

삽입과 삭제를 했으니, 탐색하는 연산은 아래와 같이 표현할 수 있다.

앞서 인덱스가 무용하다고 말한 바 있다. 즉 앞에서부터 순차 접근을 해야 하기 때문.

class Node:
    def __init__(self, key=None):
        self.key = key
        self.next = None

class SinglyLinkedList:
    def __init__(self):
        self.head = None
        self.size = 0

# insert, remove생략

	def search(self, key): #O(n)
		v = self.head
		while v != None:
			if v.key == key:
				return v
			v = v.next
		return None

	def __len__(self):
		return self.size

일방향 연결 리스트에서는 테일 노드 접근을 할 때 앞에서부터 순차적으로 접근했다.

“아, 그럼 양방향으로 접근이 가능하면? 테일이 프론트가 될 수 있지 않나?”라는 생각이 든 거지.

그럼 앞서 정의한 노드의 구성이 살짝 바뀌어야 한다. 기존에는 하나의 키와 링크만 필요했는데 이제는 오른쪽을 가리키는 next뿐만 아니라 이전 노드도 가리키는 prev도 필요해졌다. 그리고 다른 한 가지를 더 하려고 하는데, 바로, 헤드의 prev(이전 링크)는 테일을 가리키게 하고 테일의 next(이후 링크)는 헤드를 가리키게 하려고 한다.

즉, 머리와 꼬리가 맞물린 Circular Doubly Linked List라고 할 수 있다.

2. Doubly Linked List(양방향 연결리스트)

원형 연결 리스트의 빈 리스트는 시작이 어딘지를 알려주는 dummy 노드가 있어야 한다. 마커인거지. 그럼 그 더미 노드는 next가 자기자신을, prev도 자기자신을 가리키고 이제 들어오기를 대기타는 상황이라고 할 수 있다.

자 그럼 원형 연결 리스트를 위한 노드를 다시 선언을 해보자면, 아래와 같다. 

class Node:
	def __init__(self, key=None): # key 디폴트는 None
		self.key = key
		self.next = self
		self.prev = self

그럼 싱글리에서처럼 더블리 링크드 리스트도 마찬가지로 헤드를 만들어서 가리키게 하면 되겠지.

class DoublyLinkedList:
	def __init__(self):
		self.head = Node()
		self.size = 0

insert, remove

이제 설명할건, 삽입, 삭제 연산에 사용할 친구인데 굉장히 중요한 연산이다.

일방향에서는 이전 노드를 가리키는 링크가 없었기 때문에 해당 연산의 유무가 성능 향상에 크게 중요하지 않았는데 양방향에서는 이 연산으로 삽입과 노드 이동 연산을 상수 시간에 달성할 수 있게 한다.

Splice(nodeA, nodeB, nodeX)

A부터 B까지 덩어리를 잘라서 X다음에 넣는 연산이다. X는 같은 리스트 상에 있을 수도 있고 다른 리스트일 수도 있다. 이 연산을 위해서는 단순하게 6개의 링크를 바꾸면 된다.

먼저, a, b, x 3개의 노드가 필요하다.

  • 조건1: a를 계속 따라가다보면 b가 나와야 한다.
  • 조건2: a와 b사이에 헤드가 있으면 안 된다.
  • 조건3: a와 b사이에 x노드가 있어서도 안 된다.
class Node:
    def __init__(self, key=None):
        self.key = key
        self.prev = None
        self.next = None

class DoublyLinkedList:
    def __init__(self):
        self.head = Node() 
        self.size = 0

    def splice(self, a, b, x):
        if a is None or b is None or x is None:
            return 

        ap = a.prev
        bn = b.next
        xn = x.next

		# 잘라내서 
        if ap is not None:
            ap.next = bn
        if bn is not None:
            bn.prev = ap

        # 붙여넣기
        a.prev = x
        b.next = xn
        if xn is not None:
            xn.prev = b
        x.next = a

앞서 언급한 splice를 사용해서 삽입 연산을 구성하려고 한다. 먼저 삽입을 하기 위해서 이동 연산을 두 개 만들어주고 이를 이용해서 중복을 피할 수 있다.

→ 아래 코드 self가 정상적으로 들어갔는지 확인해야 함.

class DoublyLinkedList:
		# ... 생략 ...
		
		# 노드 이동시키는 연산
    def moveAfter(self, a, x):
        self.splice(a, a, x)

    def moveBefore(self, a, x):
        self.splice(a, a, x.prev)

		# 노드 삽입하는 연산
    def insertAfter(self, x, key):
        self.moveAfter(Node(key), x)

    def insertBefore(self, x, key):
        self.moveBefore(Node(key), x)

		# 앞에 삽입
    def pushFront(self, key):
        self.insertBefore(self.head, key)

    def pushBack(self, key):
        self.insertAfter(self.head, key)

탐색연산은 다음과 같다. 일방향 연결리스트와 마찬가지로 앞에서부터 순차적으로 탐색해야 하는 비효율성은 존재한다. 

	def search(self, key):
        v = self.head.next # 더미노드
        while v != self.head:
            if v.key == key: 
                return v
            v = v.next
        return None

    def remove(self, x):
        if x is None or x == self.head:
            return
        x.prev.next = x.next
        x.next.prev = x.prev
        del x

수행시간을 살펴보자.
search는 O(n), splice는 O(1), 그래서 splice 연산하는 친구들인 moveAfter/Before, insert두 개, pushFront/Back 모두 O(1)이라고 할 수 있음. remove는 코드 상으로 O(1), popFront/Back도 마찬가지로 O(1)가 걸린다.

실제로 링크드 리스트의 시간 복잡도에 대해서 검색을 하면 많은 경우 삽입과 삭제에 O(1)이 소요된다고 한다.

🤔 그런데 정말 삽입과 삭제가 O(1)인가?

맨 처음에 링크드 리스트의 강력한 특징으로, 삽입과 삭제에 상수 시간이 소요됨을 강조한 바 있다.

O(1)이긴 하다. 언제? 우리가 참조할 값들을 다 알고 있는 경우.
예를 들어 일방향 링크드 리스트의 헤드나 양방향 링크드 리스트의 헤드나 테일의 경우는 모든 리스트를 순회할 필요 없이 링크 몇개만 조정하면 된다.

그러나 임의의 위치를 가정하면 최악의 경우 O(n)의 복잡도에 해당할 수 있다.
그러나 우리가 특정 위치에 노드를 추가해야 하는데 그 위치에 대한 레퍼런스가 하나도 없는 경우는? 결국 탐색해야 하는 시간이 소요된다.
삭제도 마찬가지이다. 삭제할 노드를 넘겨주는 과정에서 탐색이 필요한 경우가 존재한다.

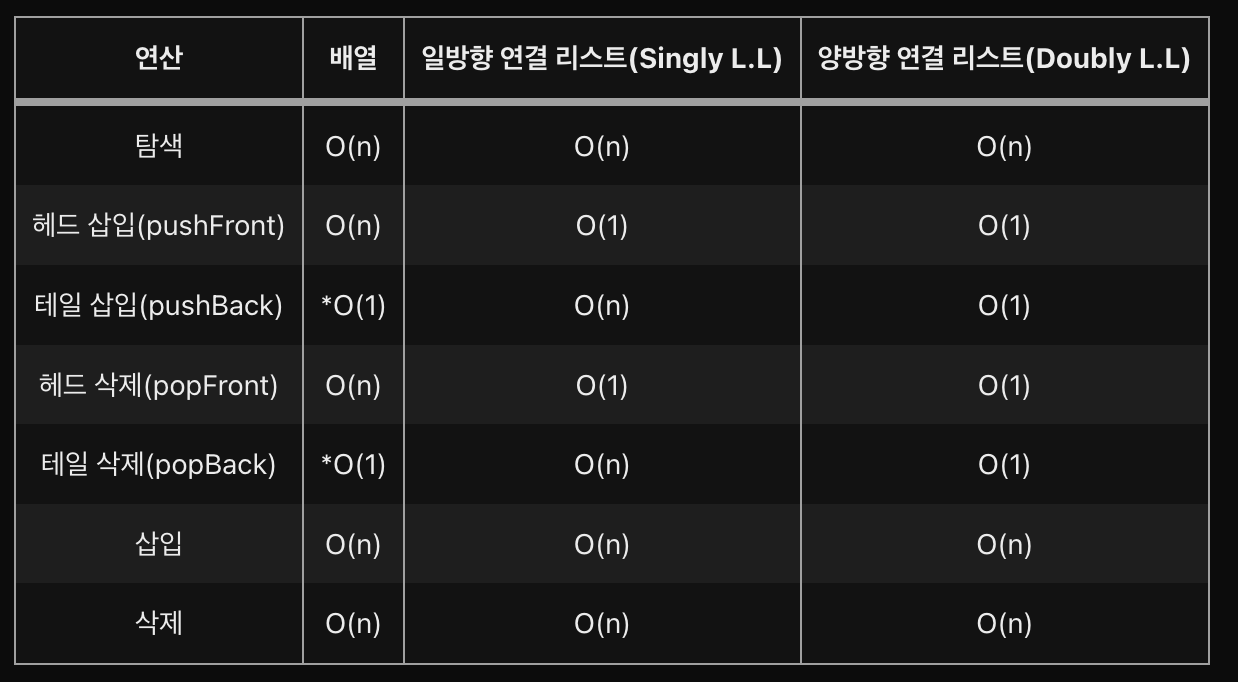
연산배열일방향 연결 리스트(Singly L.L)양방향 연결 리스트(Doubly L.L)
탐색O(n)O(n)O(n)
헤드 삽입(pushFront)O(n)O(1)O(1)
테일 삽입(pushBack)*O(1)O(n)O(1)
헤드 삭제(popFront)O(n)O(1)O(1)
테일 삭제(popBack)*O(1)O(n)O(1)
삽입O(n)O(n)O(n)
삭제O(n)O(n)O(n)

*이전 글에서 배열의 insert, remove는 O(n)으로 표기했었는데 이번에 pushBack, popBack이 O(1)인 이유는 크기 조정이 필요없는 dynamic array인 경우에는 O(1)의 복잡도를 가진다. 크기 조정에는 새 배열(일반적으로 원본 크기의 두 배)을 메모리에 할당하고 이전 배열의 모든 요소를 새 배열로 복사하는 작업이 있는데 이 작업은 모든 값을 개별적으로 복사해야 하므로 시간 복잡도가 O(n)이 된다.

profile
인마헷
비공개 글이 너무 많다...My code may sink, but at least I can swim🤿
이전 포스트

순차적 자료구조: 배열, 스택, 큐 + 리트코드로 넘어간 이유

다음 포스트

무적의 해시 테이블(Hash Table)

0개의 댓글