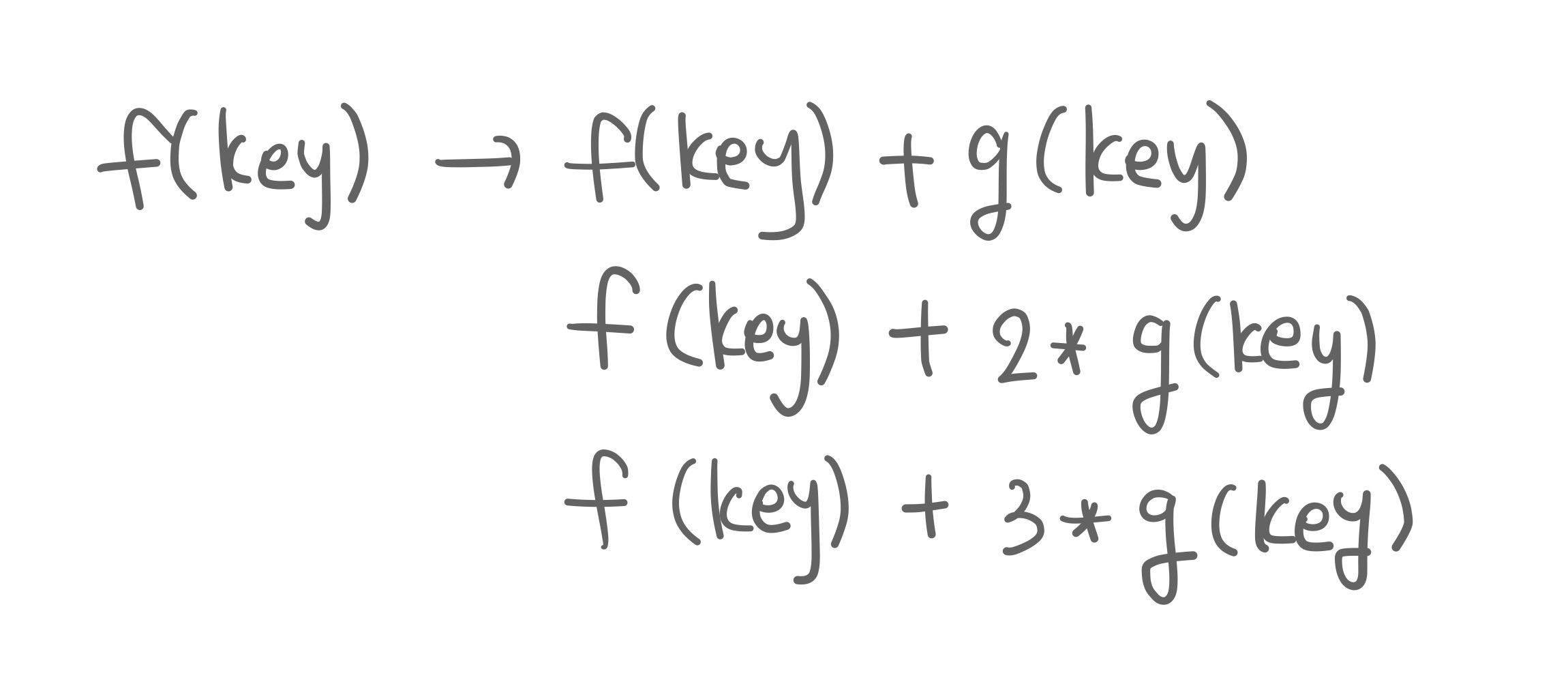“딕셔너리 쓰지 마라😠”
아니 이 좋은 걸 왜 쓰지 말라고 하냐. (살짝 끄적거림)
“뭘 알지도 못하면서. 벌써 편한 거 찾지마😡”

무적의 해시 테이블이다.

해시 테이블(hash table)

우리가 결국 자료 구조를 통해서 하고 싶은 건 자료의 삽입, 삭제, 탐색이다. 해시 테이블의 경우는 그 연산이 상수 시간에 가능한 매우 강력한 자료구조이다. (매우 빠른 “평균” 수행시간)

파이썬에서는 dict, dictionary(딕셔너리)라고 부르는 자료구조가 해시 테이블의 성격을 가지고 있다. 자바스크립트에서는 Map객체가 그 역할을 하겠다.

값들은 key와 value의 쌍으로 저장되는데 key는 본질적으로 아이템 구분을 위해 사용하기 때문에 고유한 값이어야 한다.

그럼 실제로 어떻게 저장을 하냐?

예시

• 저장하려는 데이터: { key: 1, value: name }
• 저장 공간: 0부터 9까지의 공간
• 매핑용 연산: 키 % 저장 공간의 개수 f(key) = key % 10

키 1을 가지고 인덱스 매핑용 연산을 한다. 1을 10으로 나눈 나머지는 1이니까 value : name은 인덱스1에 저장을 하고, 키가 9인 데이터는 인덱스9에 저장을 하게 되겠지.

나중에 내가 1의 키를 가진 데이터를 접근하고 싶어. 그럼 데이터를 저장할 때 수행했던 연산을 적용해서 그 인덱스 값에 가면 데이터를 찾아갈 수 있다.

이렇게 키를 가지고 인덱스로 매핑하는 연산, 함수를 해시 함수라고 한다.

그런데 만약에 11번 키가 와서 데이터 등록한대. 그럼 해시 함수를 적용하면 1이잖아. 근데 이미 1에 저장된 값이 있어. 그런 경우, 충돌(collision)이 발생하게 된다.
즉, 이 충돌을 어떻게 관리할 것인가가 해시 테이블 성능을 결정하는 핵심 요소가 되며 이 충돌을 관리하는 방법을 collision resolution method라고 한다.

해시 테이블 성능 3요소

해시 테이블의 성능을 좌우하는 3가지 요소는 다음과 같다.

1. hash table
2. hash function
3. collision resolution method

해시 테이블 관련 용어

• H: 해시 테이블
• 슬롯(Slot) 혹은 버킷(Bucket): 저장할 공간. 일반적으로 2의 N승 개로 가지고 있고 개수를 표현할 땐 m으로 표현한다.
• set(key, value): 데이터 삽입 연산이다. key가 H에 있으면 기존 값을 value로 업데이트하고 키가 없으면 그때 insert한다.
• remove(key)
• search(key)
• 클러스터: 연속적으로 저장된 데이터의 덩어리

---

Hash function

앞서 저장할 공간의 개수로 키를 나눈 나머지를 활용했었다. 그런 함수들을 해시 함수라고 하고, 특히 나머지를 사용하는 해시 함수 종류를 Division hash func.이라고 한다. 근데 이 케이스는 충돌이 자주 발생할 수 밖에 없다. 하나의 키에 집중되는 경우가 생길 수 있는데 각 슬롯에 골고루 분산되게 하는 함수를 Perfect hash func.이라고 한다.

1. perfect h.f

key → slot에 1:1로 매핑되게끔 하는 것. 굉장히 이상적인데 진짜 "이상"임.

2. universal h.f

그래서 찾은 다음 방편이 universal hash func이 있다.
Percent(f(key1) == f(key2)) = 1/m
key1와 key2에 hash func을 적용했을 때 같은 값, 즉 같은 인덱스가 나올 확률이 1/m이라는 것. 전체 해시 테이블의 사이즈에 반비례한다는 것. 이것도 구현하기가 굉장히 어렵다.

3. c-universal h.f

그래서 제한을 조금 완화하여, c/m까지는 봐주자. (c > 1)
Percent(f(key1) == f(key2)) = c/m

실제로는 이 방법을 많이 사용한다.

그 외에도…
Division, Multiplication, Folding, Mid-square, extraction 등의 다양한 hash function이 있다. 우리가 사용하는 어플리케이션이나 환경에 따라 적합한 hash func를 사용하게 될 것.
그리고 키의 타입에 따라서 몇가지 유명한 해시 함수들도 있다. (+rotating)
키가 string인 경우는 additive h.f. 키의 char를 다 더해서(아스키코드 등) 그 값을 m(해시테이블의 사이즈)로 나눈다.

결국 가장 중요한 것은 같은 슬롯에 매핑되는 충돌이 적었으면 하는 것.

좋은 해시 함수란?

1. 충돌이 적고, less collision
2. 해시 연산이 빨라야 한다.fast computation

---

Collision resolution method 01. open addressing

충돌이 발생한 슬롯 주위에 빈칸이 있을 수 있으니,
그 빈칸을 찾아서 거기에 저장하자!

그럼 그 빈칸을 찾는 방법이 또 필요하겠지. 아래 3가지가 있다.

• linear probing
• quadratic probing
• double hashing

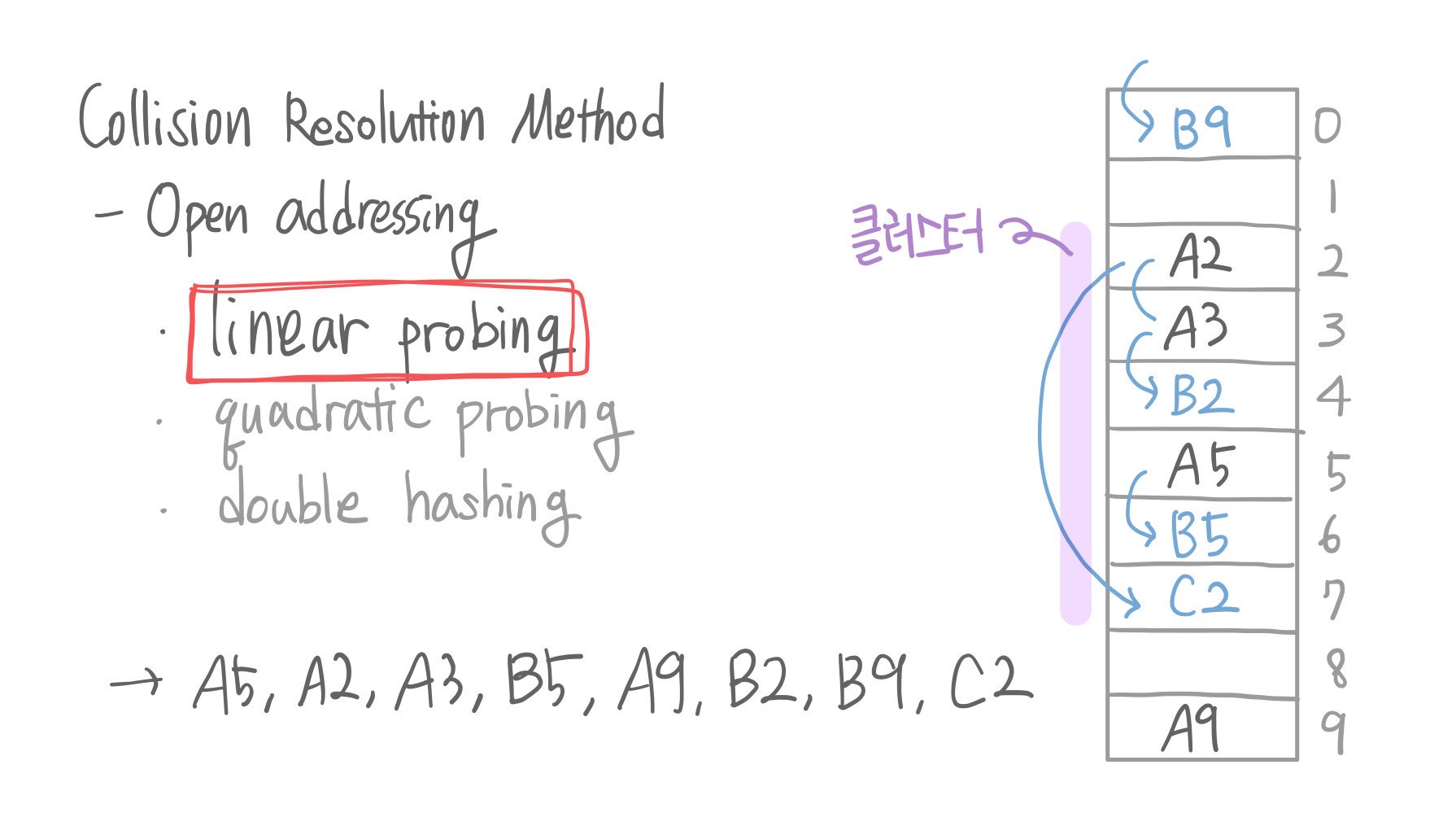
1. linear probing

한 칸씩 내려가면서 빈칸을 찾고 그 곳에 저장하는 방법인데 그럼 데이터가 모여있는 클러스터가 클 수록 불리한 방법이 된다. 원래 저장할 위치에서 한참 떨어져서 저장이 될테니까. 또한, 탐색에도 불리하다. 클러스터의 끝까지 내려가야하는, 시간이 오래걸리는 단점이 발생하게 된다.

이 클러스터를 피해야 하는데,

search(C2)를 하게 되면 C2가 없다고 가정하는게 아니라 C2를 찾을때까지 연속된 공간을 다 뒤지게 된다. 그래서 데이터를 찾으면 다행이야. 만약에 search(B3)를 찾는다고 했을 때도 있을 거라는 가정 하에 계속 내려가보는거야. 그제서야 빈칸을 만나고 '아 없네…?'하는 비효율적인 상황이 발생한다.

set, search, remove 연산

insert, search, remove는 모든 자료구조에서 공통으로 중요한 연산이라고 할 수 있는데 해시 테이블에서는 collision resolution method에 따라서 그 구현이 달라진다.

먼저 key 값이 있으면 slot번호 리턴하고, 없으면 key가 삽입될 slot번호를 리턴하는 findSlot을 정의한다.

아래는 슈도코드로 작성하였다.

findSlot(key):
    i = hashFunction(key) 
    start = i
    while table[i] is occupied and table[i].key != key:
        i = (i + 1) % tableSize
        if i == start:
            return SlotFull 
    return i

set(key, value=None):
    i = findSlot(key)
    if i == SlotFull:  # 테이블이 resize가 필요한 경우
        return None
    if table[i] is occupied:
        table[i].value = value  
    else:
        table[i].key, table[i].value = key, value 
    return key     

비교적? 간단한 위의 두 연산에 비해서 remove 함수는 훨씬 까다롭다.

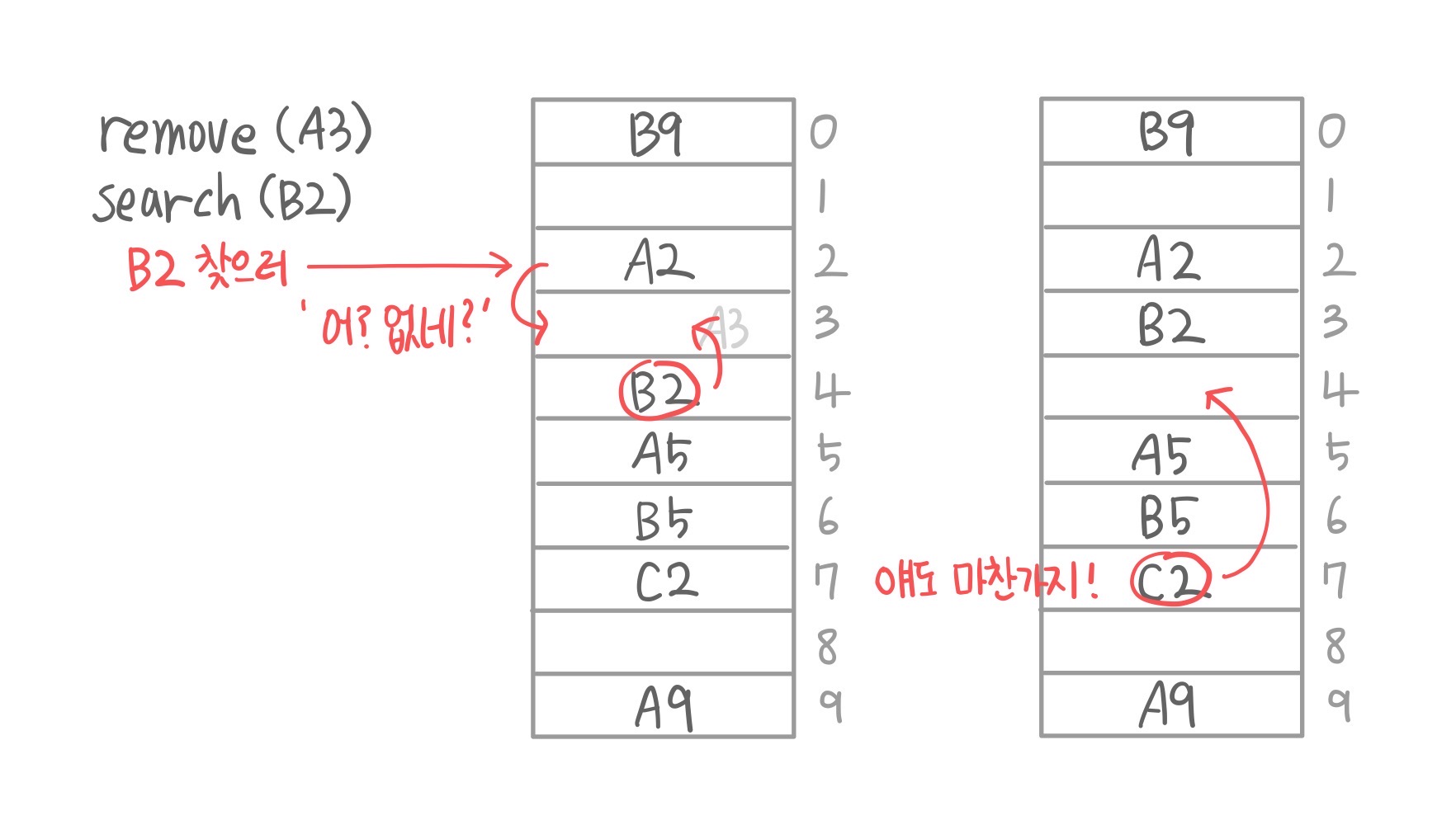
먼저 상황을 풀어보면, remove(A3)를 한다고 하자. 그럼 그냥 A3를 삭제하고 "와 됐다!" 끝이 아니게 된다. 왜냐 이 상황에서 search(B2)를 한다고 하면, B2는 A3 때문에 밀려서 4로 가게 된 친구이기 때문에 여기까지 와줘야 한다. 그런데 지금 A3만 삭제해버리면 B2찾으러 왔다가 빈칸만나고 "어 없네?" 하고 "B2는 이 테이블에 없음."이라고 결론 내려버리는 상황이 된다.
즉, 무언가를 삭제하면(linear probing에서는) 자기 자리가 없어서 밀려서 저장된 애들을 땡겨올라와 줘야 한다.

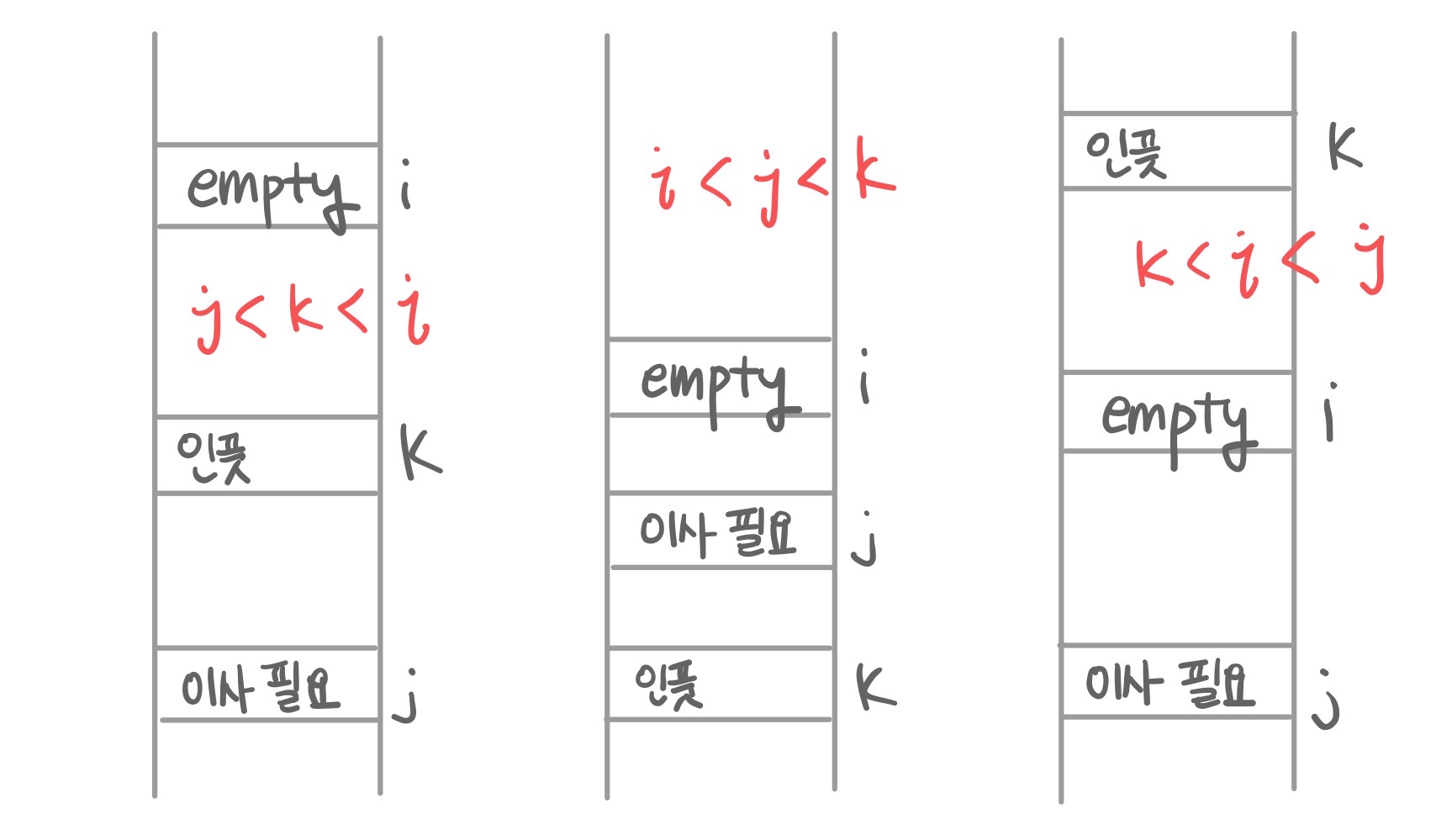
근데 이와중에 하나를 더 고려해야 하는데 우리가 지금 테이블의 양쪽이 연결된 상태임을 가정하고 있는 거니까 아래 이미지와 같이 k<i<j인 상태뿐만 아니라 j<k<i, i<j<k이 세가지 전부에 대해서 이동을 해줘야 한다.

마찬가지로 remove도 슈도코드로 작성하였다.

remove(key):
    i = findSlot(key)
    if table[i] is unoccupied:
        return None
    while True:
        table[i] = None  # 키-값 쌍 지우기
        j = i
        while True:
            j = (j + 1) % tableSize
            if table[j] is unoccupied:
                return key
            k = hashFunction(table[j].key)
            if not (k <= i < j):  
                break
            table[i] = table[j]  # 이사 시키기
            i = j

while 루프 내에서는 지금 빈 공간에 이사할 j를 찾는 과정이다.
j = (j+1)%tableSize → 하나 아래를 보는거야
table[j]가 비어있으면 오른쪽 표에서 슬롯8에 와있는거야. 그럼 다시 찾아볼 필요 없겠지.
이제 그럼 k를 해야돼. k=f(table[j].key)원래 슬롯 번호.
얘가 if (k<i<j) : break,내부의 while문을 나오고 table[i] = table[j] 해주고 i = j 해서 다시 외부의 while문을 돌아. 원래 j였던 애가 i가 됐으니 빈 슬롯 만들고 거기에 들어갈 애를 찾아야겠지. 언제까지? 슬롯8만나서 key 리턴해줄 때까지. (키를 리턴하는 이유는 "아 이사까지 다했다"를 의미함)

아이러니하게도, 클러스터 길이는 결국 키와 인덱스를 매핑해야 하는 해시 함수가 결정하게 되는데 충돌 해소 방법으로 linear probing를 적용하게 되면 계속 클러스터의 길이를 증가시키게 된다.
즉, 클러스터 증가에 역할을 크게 하기에 좋은 해싱은 아니라고 평가함.

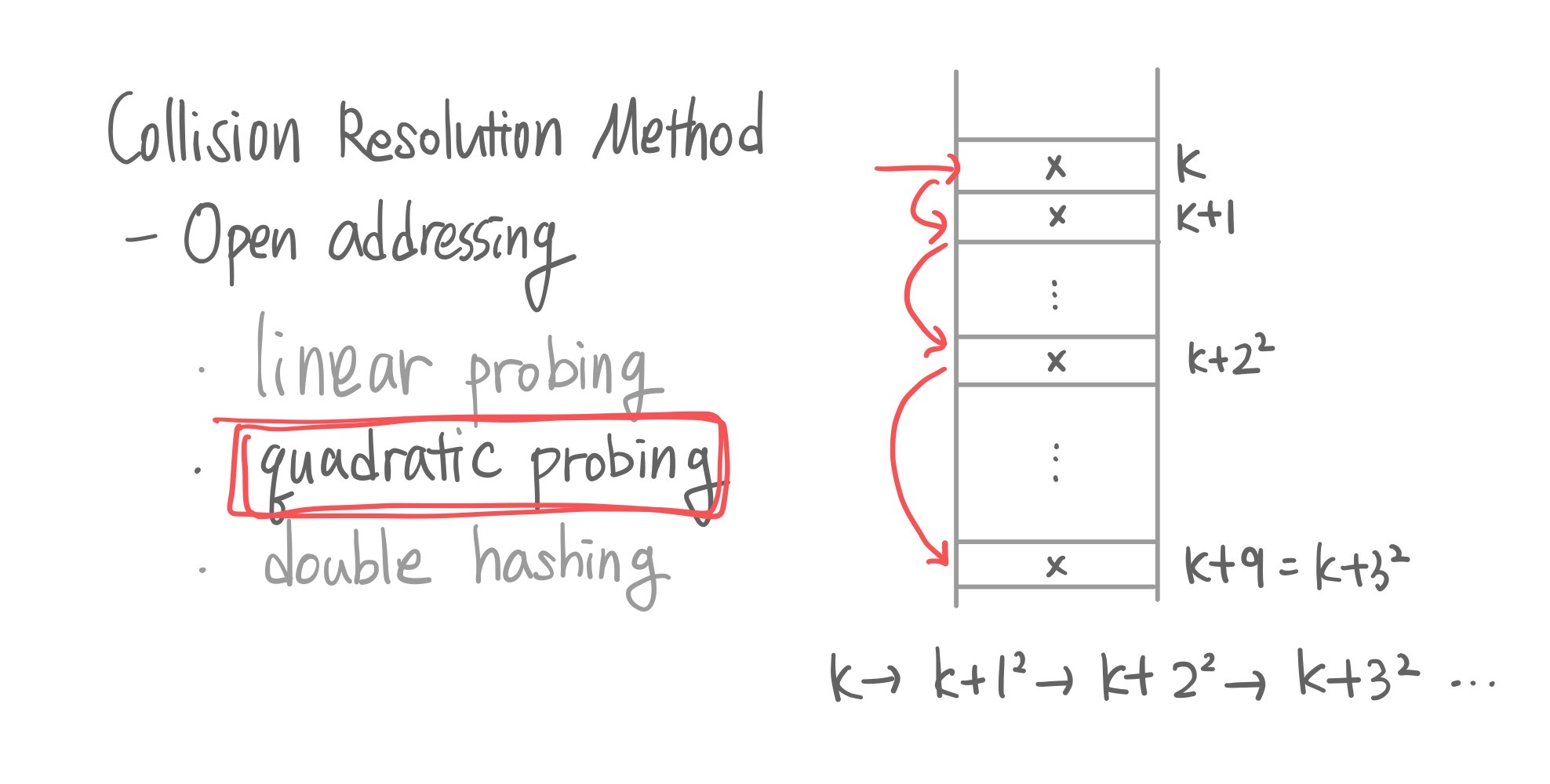
2. quadratic probing

linear의 경우는 한 칸씩 아래에 저장하는 거였잖아. quadratic은 좀 띄엄띄엄 보는데 그 간격이 2의 n승만큼 띄어서 보자는 것을 의미한다.

linear보다는 클러스터 사이즈 측면에서는 장점이 있을 수 있는데 나중에 remove 함수 작성할 때 환장할 수 있다.

3. double hashing

이번엔 해시 함수 하나로는 안 될 것 같으니, 해시 함수를 두 가지 사용해보자는 논의이다.

만약에 데이터를 저장하려는 슬롯이 이미 차 있으면 다른 해시 함수(g(key))를 한 것을 더해. 만약에 거기도 차 있으면 다른 해시 함수(g(key)) 값을 2배해서 더하고, 3배해서 더하고, 그렇게 증가시키는 방법이다.

문제는 해시 연산을 두 번 해야 하는 것과 그 함수를 두 가지 마련해야 한다는 것이 있겠다.

그럼 어떤 방법이 성능 측면에서 효율적일까?

해시 테이블의 3가지 연산, set, remove, search이 3가지는 클러스터 사이즈에 영향을 받았다. 그 클러스터 사이즈는 해시 함수와 collision resolution method에 영향을 받았고.
그런데 이것 외에도 중요하게 고려해야 하는 것이 load factor이다.

load factor?

로드계수라고 번역하기도 한다. n/m, 해시테이블에 저장된 아이템 개수가 n이고 해시테이블의 사이즈가 m이다. 즉 n/m은 0이상, 1이하의 값.

load factor가 작으면 빈 슬롯이 더 많다는 이야기이고 그럼 충돌 발생 가능성이 적어진다.

load factor를 일정 수준으로 유지하기 위해 테이블의 사이즈를 동적으로 조정하면 되지 않을까?

해시 테이블 동적 확장(Resize)

open addressing은 클러스터 사이즈에 의해서 영향을 받는데 평균적으로, 최소 50% 정도는 빈 슬롯을 유지한다고 가정하면 (두배 더 큰 해시 테이블을 만들어서 이사를 하는 것) 이사 비용을 다 합치더라도 클러스터의 평균 사이즈가 O(1)이 되게 할 수 있다.

즉, 사이즈가 m인 테이블이 있는데, 평균적으로 일정 수준 정도만 차 있게 관리를 해주면 클러스터의 사이즈가 상수 선에서 끝난다는 것. 그럼 세 가지 연산이 클러스터 사이즈에 비례해서 걸리기 때문에 그 모든 것이 O(1)이 된다는 것이다.

그럼 일정수준은 무엇일까? 해시를 확장하는 임계점은 현재 데이터 개수(n)가 해시 슬롯(버킷)의 개수(m)의 75%가 될 때이다. 그래서 여기서의 로드 계수는 0.75가 된다.

---

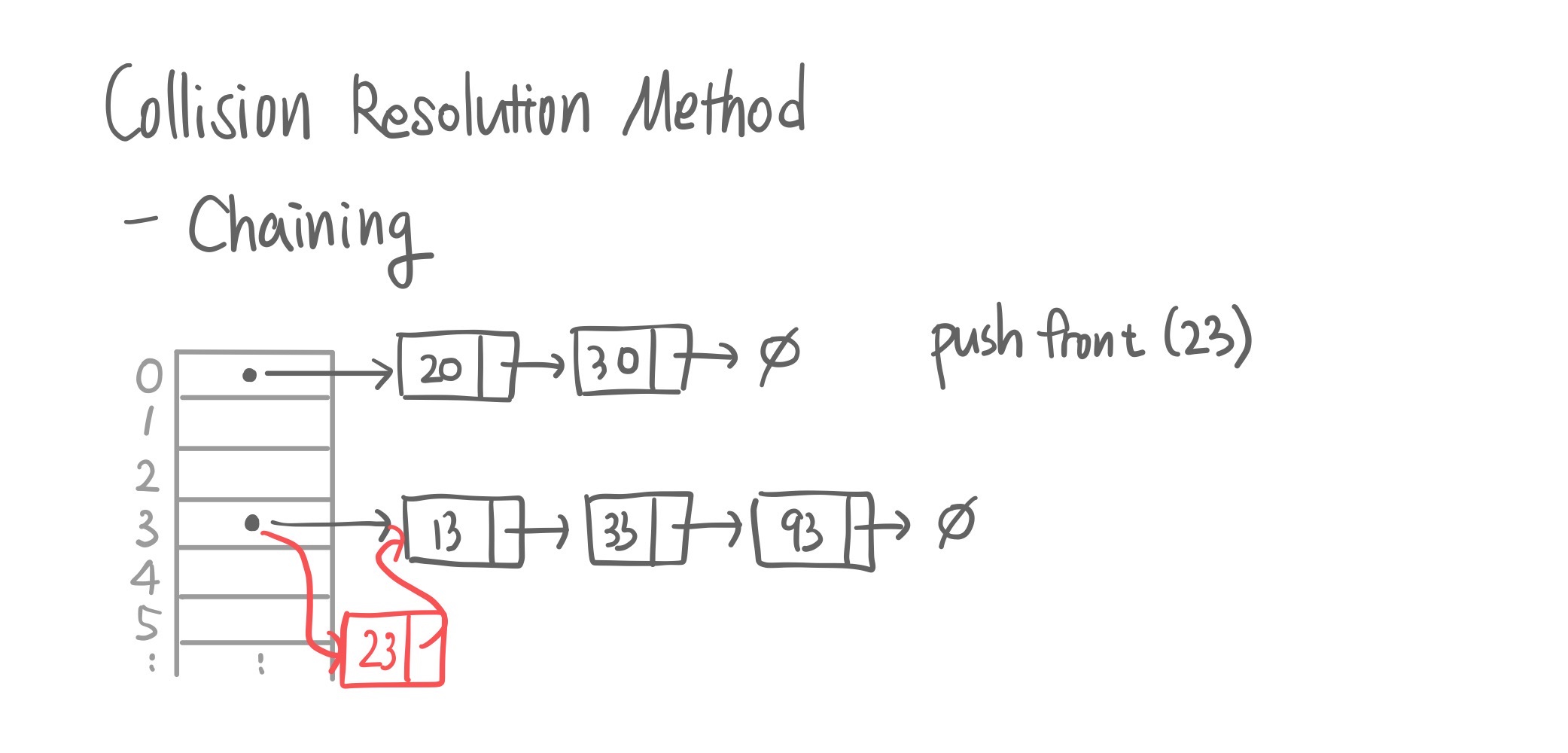
Collision resolution method 02. chaining

왜 굳이 다른 데에 저장해? 하나의 슬롯에 여러 개의 아이템을 저장하자!

open addressing은 다른 슬롯을 굳이굳이 찾아가서 저장을 했는데 이번에는 원래 자리에 저장하자는 주장이다. 어떻게? 각 슬롯에 링크드 리스트를 만든다.(Singly Linked List)

그리고 데이터가 오면 pushFront() 함수를 호출하는 것, 이게 O(1)시간에 가능하기 때문에 set()도 마찬가지로 O(1)에 가능할 것이다.

search(23)이라면 해당하는 슬롯에 가서 서치를 하면 된다. 발생할 수 있는 최악의 경우는 해당되는 슬롯의 충돌 키의 평균 개수(linked list의 길이)가 된다. remove도 결국 search를 해야 하기 때문에 마찬가지.

즉, 이 linked list를 사용하기 위해서는 해시 함수를 잘 골라 써야 하는데 c-universal 해시 함수를 사용해야 한다. 이렇게 되면 평균적으로 충돌하는 키의 개수가 상수 개를 유지하고, 슬롯당 평균 Linked list의 길이도 상수개를 유지한다. 즉, 골고루 분포가 된다는 것. O(1)

---

Open Addressing vs Separate Chaining

open addressing

• 모든 데이터가 배열 자체에 저장되므로 링크드 리스트를 위한 추가 공간이 필요없음
• 모든 데이터가 배열에 직접 매핑되므로 캐시 성능이 향상되어 참조 위치 정확

그러나

• 채워진 슬롯이 클러스터를 형성하는 경향
• 로드 팩터에 따라 성능이 저하
• 앞서 봤듯이 삭제가 복잡함

chaining

• 구현 간단, 충돌과 삭제를 처리할 때 유용
• 클러스터링 감소: 충돌 해결이 메인 테이블 외부에서 처리
• load factor가 1보다 큰 경우에도 우수한 성능을 발휘할 수 있음

그러나

• 링크드 리스트를 위한 추가 공간 필요
• 여러 데이터 구조가 사용되어 캐시 성능이 저하
• 해시 함수가 키를 잘 분배하지 않으면 일부 체인이 다른 체인보다 훨씬 길어짐

그래서 결론이 뭔데?

결국 해시 함수는 c-universal 함수를 사용하고 충분한 길이의 빈 슬롯을 유지한다고 하면 chaining이든 open addressing이든 O(1)으로 중요한 3가지 연산을 할 수 있는 매우 강력한 자료구조이다.

---

연산 별 시간 복잡도

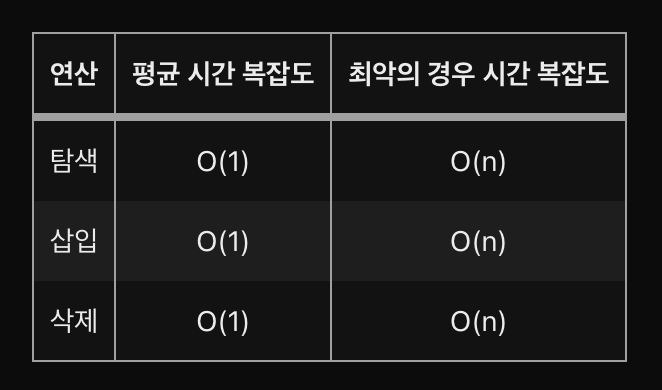
연산	평균 시간 복잡도	최악의 경우 시간 복잡도
탐색	O(1)	O(n)
삽입	O(1)	O(n)
삭제	O(1)	O(n)

해시 테이블은 평균적으로 검색, 삽입, 삭제에 대해 일정한 시간 복잡성인 O(1)을 제공하도록 설계된다. 버킷 전체에 키를 균일하게 분배하는 해시 함수가 큰 역할을 한다.

---

그럼 저장공간을 살 돈이 많으면 되겠다...!🤑