[프로그래머스 / C++] 정수 삼각형 : DP

https://programmers.co.kr/learn/courses/30/lessons/43105

문제 풀이

가장 기본적인 DP문제인 것 같다.
DP를 푸는 방법은 2가지가 존재한다.

1. 점화식을 이용하는 Bottom-Up 방식
   • 직관적으로 알 수 있는 시작점은 미리 dp배열에 저장해놓는다.
2. 점화식에서 재귀(dfs), 메모이제이션을 사용하는 Top-down방식.
   • 직관적으로 알 수 있는 지점이 dfs를 중지 시키는 지점

입력값인 triangle 배열을 살피면 다음과 같다.

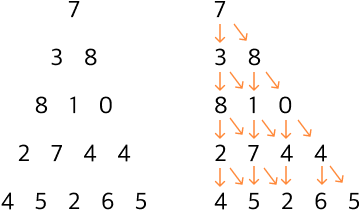
dp[i][j]를 (i,j) 좌표까지의 경로중, 가장 큰 숫자 합이라고 지정하자. 점화식은 다음과 같아진다.

dp[i][j]=max(dp[i-1][j], dp[i-1][j-1]) + triangle[i][j] (단, j=0이거나 J=i 일 때는 조건 추가)

코드

1) Bottom-Up

#include <string>
#include <vector>
#include <algorithm>
using namespace std;
const int MAX=501;

int dp[MAX][MAX];

int solution(vector<vector<int>> triangle) {
    int answer = 0;
    
    //초기 지정.
    dp[0][0]=triangle[0][0];
    
    for(int i=1;i<triangle.size();i++){
        for(int j=0;j<=i;j++){
            //1) 행에서 젤 왼쪽인 경우엔 바로 위에꺼
            if(j==0) dp[i][j]=dp[i-1][j]+triangle[i][j];
            //2) 행에서 젤 오른쪽인 경우엔 왼쪽 위에꺼
            else if(j==i) dp[i][j]=dp[i-1][j-1]+triangle[i][j];
            //나머지
            else dp[i][j]=max(dp[i-1][j-1], dp[i-1][j])+triangle[i][j];
            
            answer=max(answer,dp[i][j]);

        }
        
    }
    
    return answer;
}

2) Top-bottom

#include <string>
#include <vector>
#include <algorithm>
using namespace std;
const int MAX=501;

int dp[MAX][MAX];
int tmp[MAX][MAX];


int dfs(int r, int c){
    
    //✨dfs를 멈추는 지점 -> 직관적으로 알 수 있는 지점!
    if(r==0&&c==0) return tmp[0][0];
    
    //✨메모이제이션. 이미 계산된 결과가 있는 경우 저장 된 값 반환
    if(dp[r][c]>0) return dp[r][c];
    
    //1) 행에서 젤 왼쪽인 경우
    if(c==0) return dp[r][c]=dfs(r-1,c)+tmp[r][c];
    //2) 행에서 제일 오른쪽인 경우
    if(c==r) return dp[r][c]=dfs(r-1,c-1)+tmp[r][c];
    //3) 나머지
    else return dp[r][c]=max(dfs(r-1,c),dfs(r-1,c-1))+tmp[r][c];
    
}

int solution(vector<vector<int>> triangle) {
    int answer = 0;

    // triangle을 dfs의 인자로 넘기면 시간초과 나버림!
    for(int i=0;i<triangle.size();i++){
        for(int j=0;j<=i;j++){
            tmp[i][j]=triangle[i][j];
        }
    }
    
    // 제일 밑 행
    for(int i=0;i<triangle.size();i++){
        answer=max(answer, dfs(triangle.size()-1, i));
    }
    
    return answer;
}