👀 'Do it! 알고리즘 코딩테스트 with Python(김종관 저)'을 공부하고 정리한 내용입니다.

1. 유클리드 호제법

유클리드 호제법은 두 수의 최대 공약수를 구하는 알고리즘입니다.
일반적으로 최대 공약수를 구하는 방법은 소인수 분해를 이용한 공통된 소수들의 곱으로 표현할 수 있지만, 유클리드 호제법은 좀 더 간단한 방법을 제시합니다.

유클리드 호제법의 핵심 이론

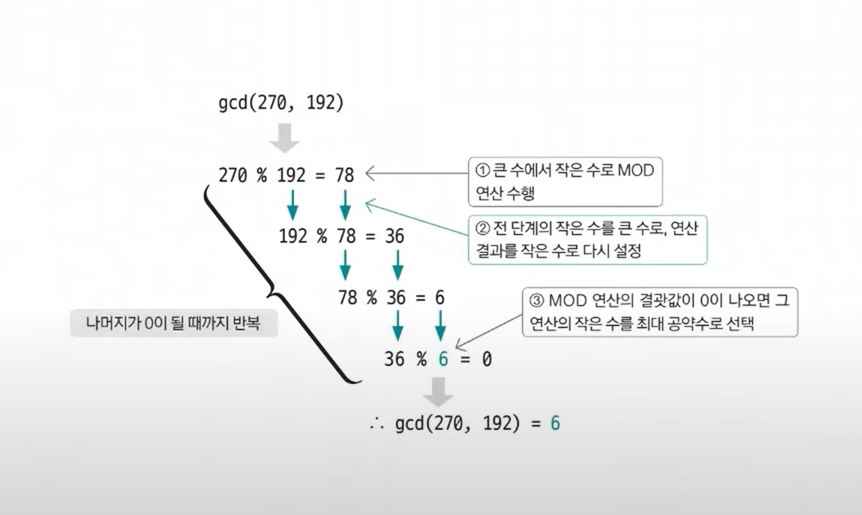
유클리드 호제법을 수행하려면 먼저 MOD 연산을 이해해야 합니다.
MOD 연산이 최대 공약수를 구하는데 사용되는 핵심 연산이기 때문입니다.

MOD연산: 두 값을 나눈 나머지를 구하는 연산, 파이썬에서 %연산과 같음.

1. 큰 수를 작은수로 나누는 MOD연산을 수행한다.
   2, 앞 단계에서의 작은 수와 MOD 연산 결과값으로 MOD연산을 수행한다.
2. 2를 반복하다가 나머지가 0이 되는 순간의 작은 수를 최대 공약수로 선택한다.

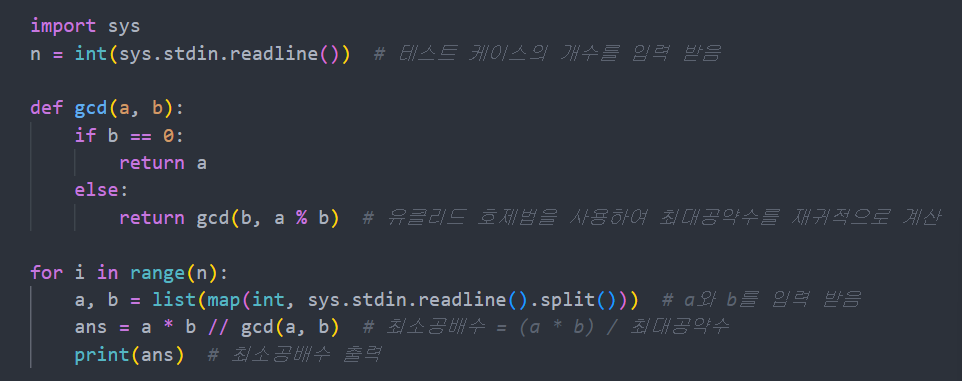
예시 문제 BOJ 1934 최소 공배수 구하기

문제

두 자연수 A와 B에 대해서, A의 배수이면서 B의 배수인 자연수를 A와 B의 공배수라고 한다. 이런 공배수 중에서 가장 작은 수를 최소공배수라고 한다. 예를 들어, 6과 15의 공배수는 30, 60, 90등이 있으며, 최소 공배수는 30이다.

두 자연수 A와 B가 주어졌을 때, A와 B의 최소공배수를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 테스트 케이스의 개수 T(1 ≤ T ≤ 1,000)가 주어진다. 둘째 줄부터 T개의 줄에 걸쳐서 A와 B가 주어진다. (1 ≤ A, B ≤ 45,000)

출력

첫째 줄부터 T개의 줄에 A와 B의 최소공배수를 입력받은 순서대로 한 줄에 하나씩 출력한다.

입출력 예

내 풀이