👀 'Do it! 알고리즘 코딩테스트 with Python(김종관 저)'을 공부하고 정리한 내용입니다.

소수란, 1과 자기 자신 외에 약수가 존재하지 않는 수를 말합니다.

종종 알고리즘 문제 중 소수를 이용한 문제가 있습니다.

소수 판별 또는 소수 갯수 구하기 등은 기본 중의 기본이니, 한 입 하고가면 든든할 것 같습니다.

1. 에라토스테네스의 체

에라토스테네스의 체는 소수를 구하는 대표적인 방법입니다.

과정은 다음과 같습니다.

1. 구하고자 하는 소수의 범위만큼 1차원 배열을 생성한다.

2. 2부터 시작하고 현재 숫자가 지워지지 않을 때는 현재 선택된 숫자를 제외한 배수를 배열에서 끝까지 탐색하면서 지웁니다.

3. 배열의 끝까지 2를 반복하면, 배열에서 남아있는 수는 모두 소수입니다.

Q. 이거 시간복잡도 많이 잡아먹을거 같은데요

일반적으로 이거 구현하려면 이중 for문을 이용하므로 그럴 것 같습니다.

하지만, 일반적으로 시간복잡도는 O(Nlog(logN)) 입니다.

그 이유는 배수를 삭제하는 연산으로 실제 바깥 for문을 돌릴때 이미 삭제된 수가 많기 때문입니다.

2. 오일러 피

오일러 피 함수 P[N]의 정의는 1부터 N까지의 범위에서 N과 서로소인 자연수의 개수를 뜻합니다.

ϕ(1) = 1 (1은 1과 서로소)

ϕ(8) = { 1, 3, 5, 7 } = 4개

ϕ(13) = = 12개

ϕ(13) = = 12개

ϕ(15) = = 8개 

과정은 다음과 같습니다.

1. 구하고자 하는 오일러 피의 범위만큼 배열을 자기 자신의 인덱스 값으로 초기화한다.

2. 2부터 시작해 현재 배열의 값과 인덱스가 같으면(= 소수라면) 현재 선택된 숫자(K)의 배수에 해당하는 수를 배열에 끝까지 탐색하며 P[i] = P[i] - P[i]/K 연산을 수행한다(i는 K의 배수).

3. 배열의 끝까지 2를 반복하여 오일러 피 함수를 완성한다.

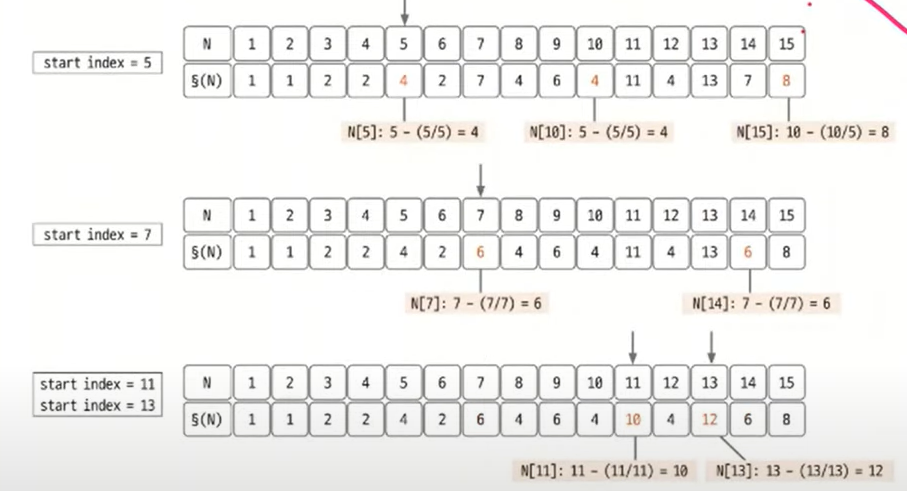
자세한 과정은 아래를 봅시다.

오일러 피 수행 과정

1. 구하고자 하는 범위까지 배열을 생성한 후 2를 선택합니다.

2. 2의 모든 배수마다 P[i] = P[i] - P[i]/2 연산을 수행해 갱신합니다. 예를 들어 8 = 8-(8/2)를 통해 4를 계산합니다.

3. 소수 구하기에서 배수를 지우는 부분만 P[i] = P[i] - P[i] / K로 변경하면 오일러 피 함수를 간단히 구현할 수 있습니다. 탐색을 계속 진행하면서 N = ϕ(N)인 곳(소수)을 찾아 값을 갱신합니다.

4. 배열이 끝날 때까지 반복합니다.