👀 'Do it! 알고리즘 코딩테스트 with Python(김종관 저)'을 공부하고 정리한 내용입니다.

1. 개념

조합은 $_{n}C_{r}$로 표현하고, 이는 n개의 숫자에서 r개를 뽑는 경우의 수를 뜻합니다. 조합과 비교되는 순열은 $_{n}P_{r}$로 표현되고, n개의 숫자중 r개를 뽑는 순서를 고려해 나열할 경우의 수를 이야기합니다. 순열과 조합의 차이는 순서의 고려 유무입니다. 즉, 조합에서는 데이터 1,2,3과 3,2,1을 같을 경우로 판단하고, 순열은 다른 경우로 판단합니다.

순열의 수학적 공식은 위와 같습니다.
단순히 5개중 2개를 고르는 경우의 수는 5*4 = 20가지로, 이 내용을 공식화 한 것 뿐입니다.

조합의 수학적 공식은 위와 같습니다. 순열과 매우 비슷하며 분모에 r!만 추가돼 있는 것을 볼 수 있습니다. r!가 의미하는 것은 순서가 다른 경우의 수를 제거하는 것 입니다. 예를 들어 5개중 2개를 선택하는 경우의 수를 구할 때, 기존 순열의 경우의 수에 2!로 나누어 5*4 / 2 = 10가지 인 것을 알 수 있습니다.

2. 이해하기

알고리즘에서 조합을 구현할 때는 위의 수학 공식을 코드화하지 않고 점화식을 사용해 표현합니다. 조합의 점화식을 아래의 3단계로 세워보겠습니다.

2-1. 특정 문제를 가정하기

먼저 적당한 조합문제를 가정해봅니다. 5개의 데이터에서 3개를 선택하는 조합의 경우의 수를 푸는 문제로 가정해보겠습니다.

2-2. 모든 부분 문제가 해결된 상황이라고 가정하고 지금 문제 생각하기

모든 부분 문제가 해결된 상황이라고 가정해보겠습니다. 먼저 5개의 데이터 중 4개를 이미 선택이 완료된 데이터라고 가정합니다. 그리고 마지막 데이터의 선택 여부에 따른 경우의 수를 계산합니다. 만약 마지막 데이터를 포함해 총 3개의 데이터를 선택하려면 선택이 완료됐다고 가정한 4개의 데이터에서 2개를 선택해야 합니다. 마지막 데이터를 포함하지 않고 총 3개의 데이터를 선택하려면 이전 데이터 4개 중 3개를 선택해야 합니다. 2가지 경우의 수를 합치면 데이터 5개중 3개를 선택하는 경우의 수가 나옵니다.

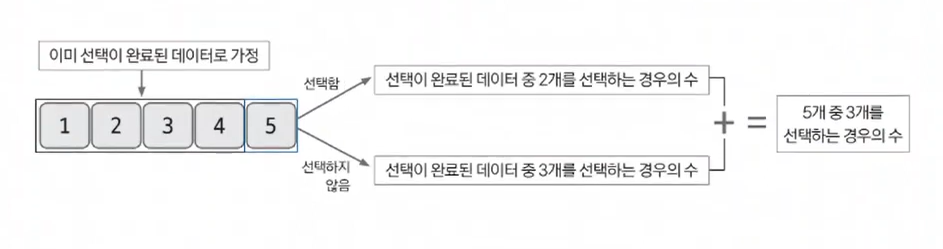
앞 그림을 점화식으로 표현하면 다음과 같습니다.

5개 중 3개를 선택하는 경우의 수 점화식
D[5][3] = D[4][2] + D[4][3]
$_{5}C_{3} = _{4}C_{2}+_{4}C_{3}$

2-3. 특정 문제를 해결한 내용을 바탕으로 일반 점화식 도출하기

이 일반화된 점화식을 이용하면 조합과 관련된 모든 경우의 수를 쉽게 구할 수 있습니다.

조합 점화식
D[i][j] = D[i-1][j-1] + D[i-1][j]

11051 이항 계수 2

문제

자연수 $N$과 정수 $K$가 주어졌을 때 이항 계수 $\binom{N}{K}$를 10,007로 나눈 나머지를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 $N$과 $K$가 주어진다. (1 ≤ $N$ ≤ 1,000, 0 ≤ $K$ ≤ $N$)

출력

$\binom{N}{K}$를 10,007로 나눈 나머지를 출력한다.

입출력 예

내 풀이 (시간 초과)

from itertools import combinations as cb

a, b = map(int, input().split())

ls = list(range(a))

tmp = cb(ls, b)
cnt = 0
for _ in tmp:
    cnt += 1

print(cnt % 10007)

강의 내 풀이

N, K = map(int, input().split())
D = [[0 for j in range(N+1)] for i in range(N+1)]

for i in range(0, N+1):
    D[i][0] = 1
    D[i][i] = 1

for i in range(2, N+1):
    for j in range(1, i):
        D[i][j] = (D[i-1][j-1] + D[i-1][j]) % 10007

print(D[N][K])