👀 'Do it! 알고리즘 코딩테스트 with Python(김종관 저)'을 공부하고 정리한 내용입니다.

1. 개념

트리 그래프에서 임의의 두 노드를 선택했을 때 두 노드가 각각 자신을 포함해 거슬러 올라가면서 부모 노드를 탐색할 때 처음 공통으로 만나게 되는 부모 노드를 최소 공통 조상이라고 합니다.
트리의 높이가 크지 않을때 보통 탐색은 DFS, BFS를 이용해 수행합니다.

2. 원리 이해하기

아래와 같은 트리에서 4번, 15번 노드의 최소 공통 조상을 구해 보겠습니다. 먼저 루트 노드에서 탐색을 시작해 각 노드의 부모 노드와 깊이를 저장합니다.

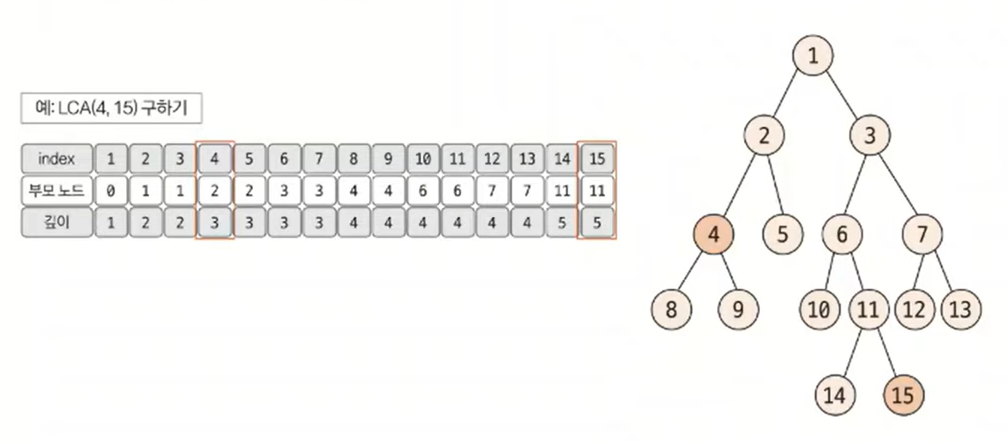
선택된 두 노드의 깊이가 다른 경우, 더 깊은 노드의 노드를 부모 노드로 1개씩 올려주면서 같은 깊이로 맞춥니다. 이때 두 노드가 같으면 해당 노드가 최종 공통 조상이므로 탐색을 종료합니다.

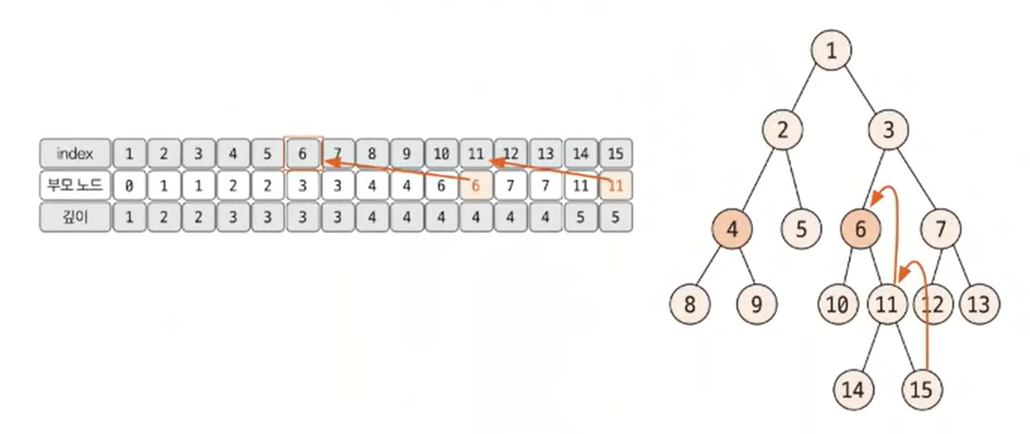
깊이가 같은 상태에서는 동시에 부모 노드로 올라가면서 두 노드가 같은 노드가 될 때까지 반복합니다. 이때 처음 만나는 노드가 최소 공통 조상이 됩니다. 이러한 원리로 다음 트리에서 4번, 15번 노드의 최소 공통 분모는 1이 됩니다.

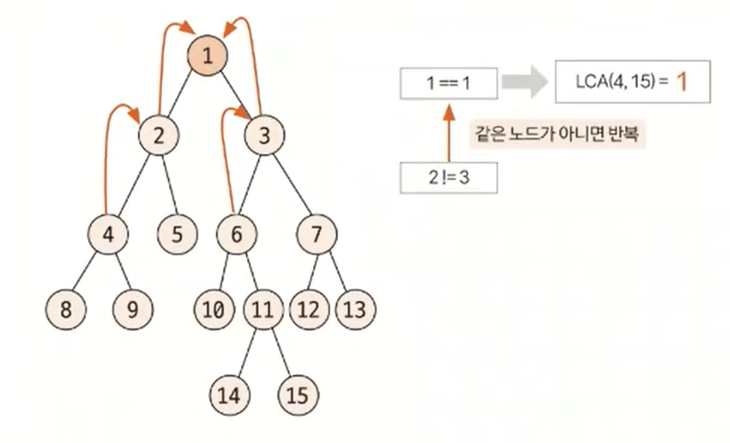
이러한 방식을 이용하면 최소 공통 조상을 구할 수 있지만 트리의 높이가 커질 경우 시간 제약 문제에 직면할 수 있습니다. 이러한 문제를 해결하기 위해 새롭게 제안된 방식이 바로 '최소 공통 조상 빠르게 구하기' 입니다. 이것은 일반적인 최소 공통 구하기 알고리즘을 약간 변형한 형태입니다.

3. 조상님 빠르게 구하기

최소 공통 조상 빠르게 구하기의 핵심은 서로의 깊이를 맞춰 주거나 같아지는 노드를 찾을 때 기존에 한 단계씩 올려주는 방식에서 $2^k$씩 올라가 비교하는 방식입니다. 따라서 기존에 자신의 부모 노드에만 저장해 놓던 방식에서 $2^k$번째 위치의 부모 노드까지 저장해 둬야 합니다.

아래 3단계를 이용해 좀 더 자세히 알아보겠습니다.

3-1. 부모 노드 저장 배열 만들기

부모 노드 배열을 만들기 위해서는 이 배열의 정의와 점화식을 알아야합니다.

부모 노드 배열의 정의
$P[K][N] = N$번 노드의 $2^k$번째 부모의 노드 번호

부모 노드 배열의 점화식
$P[K][N]=P[K-1][P[K-1][N]]$

점화식에서 N의 $2^k$번째 부모 노드는 N의 $2^k-1$번째 부모 노드의 $2^k-1$번째 부모노드라는 의미입니다. 즉, K=4 라고 가정하면 N의 16번째 부모 노드는 N의 8번째 부모 노드의 8번째 부모 노드라는 의미입니다.

배열에서 K는 트리의 깊이$> 2^k$를 만족하는 최대값입니다. 다음 트리에서 최대 깊이는 5이기 때문에 K = 2가 됩니다. 즉, 이 트리의 모든 노드는 $2^3$번째 부모 노드를 지닌 경우가 없습니다.

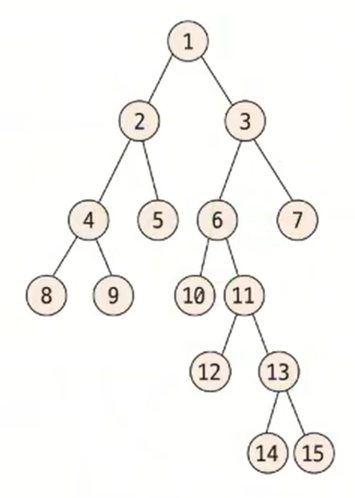
부모 노드 배열의 점화식을 이용해 배열의 값을 채워보면,

초기화된 배열을 바탕으로 K를 1개씩 증가시키면서 나머지 배열을 채웁니다. 이해를 돕기위해 14의 $2^2$번째 즉 4번째 부모노드(P[2][14])를 예시로 구해보겠습니다.

3-2. 선택된 두 노드의 깊이 맞추기

P 배열을 이용해 기존에 한 단계씩 맞췄던 깊이를 $2^k$ 단위로 넘어가면서 맞춥니다. 예를 들어 노드 2와 노드 15의 깊이를 맞춰보겠습니다. 노드 2의 깊이는 2, 노드 15의 깊이는 6으로 두 노드의 깊이 차이는 4입니다. 깊이를 맞추기 위해 더 깊이 있는 노드 15의 4번째 부모 노드를 P 배열을 이용해 찾습니다. $4=2^2$이므로 K=2이고, P[2][15]=3이므로 노드 3으로 이동하면 노드 2와 높으를 맞추게 됩니다.

만약 높이 차지가 20이라고 가정하면 $2^k\le20$을 만족하면서 K가 최대가 되는 만큼 이동하면서 높이 차이가 0이 될때까지 반복합니다. 즉, 높이 차이가 20일 경우에는 $2^4(16)→2^2(4)$와 같이 두 번 이동하면 됩니다.

3-3. 최소 공통 조상 찾기

공통 조상을 찾는 작업 역시 한 단계씩이 아닌 $2^k$ 단위로 점프하면서 맞춥니다. K값을 1씩 감소하면서 P 배열을 이용해 최초로 두 노드의 부모가 달라지는 값을 찾습니다.

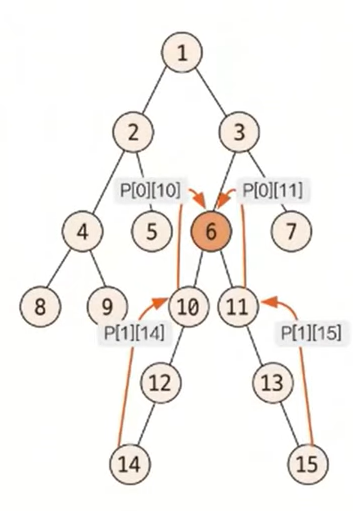
최초로 달라지는 k에 대한 다 노드의 부모 노드를 찾아 이동합니다. 즉 노두 10, 노드 11로 이동합니다. 이를 K가 0이 될때까지 반복합니다. 반복문이 종료된 후 이동한 2개의 노드가 같은 노드라면 해당 노드가, 다른 노드라면 바로 위의 부모 노드가 최소 공통 조상이 됩니다. 여기에서는 노드10, 11이 다른 노드이기 때문에 바로 위 노드를 뜻하는 P[0][10] 또는 P[0][11] 즉, 노드 6이 최소 공통 조상이 됩니다.