👀 'Do it! 알고리즘 코딩테스트 with Python(김종관 저)'을 공부하고 정리한 내용입니다.

1. 개념

트리는 노드와 이제로 연결된 그래프의 특수한 형태입니다.
트리가 가진 특징은 다음과 같습니다.
첫째, 순환 구조를 지니지 않고, 1개의 루트 노드가 존재합니다.
둘째, 루트 노드를 제외한 모든 노드는 단 1개의 부모 노드를 갖습니다.
셋째, 트리의 부분 트리 역시 트리의 모든 특징을 따릅니다.

1-1. 트리의 구성 요소

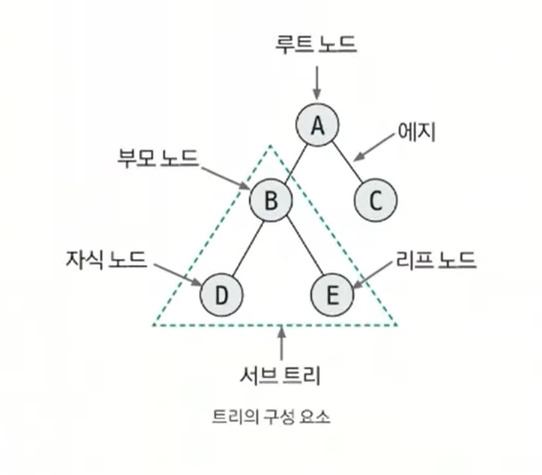
• 노드: 데이터의 index와 value를 표현하는 요소
• 에지: 노드와 노드의 연결 관계를 나타내는 선
• 루트 노드: 트리에서 가장 상위에 존재하는 노드
• 부모 노드: 두 노드 사이의 관계에서 상위 노드에 해당하는 노드
• 자식 노드: 두 노드 사이의 관계에서 하위 노드에 해당하는 노드
• 리프 노드: 트리에서 가장 하위에 존재하는 노드(자식 노드가 없는 노드)
• 서브 트리: 전체 트리에 속한 작은 트리

BOJ 11725 트리의 부모 찾기

문제

루트 없는 트리가 주어진다. 이때, 트리의 루트를 1이라고 정했을 때, 각 노드의 부모를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 노드의 개수 N (2 ≤ N ≤ 100,000)이 주어진다. 둘째 줄부터 N-1개의 줄에 트리 상에서 연결된 두 정점이 주어진다.

출력

첫째 줄부터 N-1개의 줄에 각 노드의 부모 노드 번호를 2번 노드부터 순서대로 출력한다.

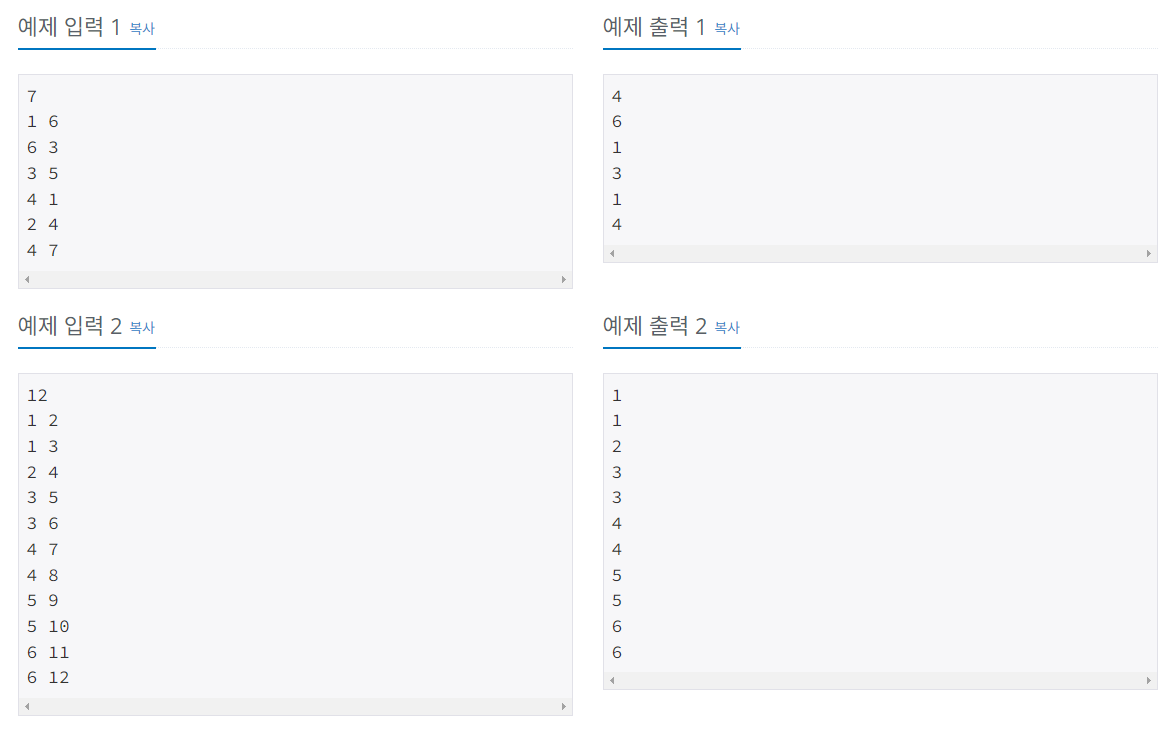
입출력 예

내 풀이 (재귀 없이 반복문으로 푸러씀!)

def find_parents(n, edges):
    tree = [[] for _ in range(n+1)]  # 각 노드의 인접 리스트 그래프를 생성합
    parents = [0] * (n+1)  # 각 노드의 부모를 저장할 리스트를 초기화
    
    for a, b in edges:
        tree[a].append(b)  # 주어진 간선 정보를 바탕으로 인접 리스트 그래프를 생성
        tree[b].append(a)
    
    stack = [1]  # 스택을 준비하고 1번 노드를 시작으로 설정
    
    while stack:
        node = stack.pop()  # 스택에서 노드를 하나 꺼내기
        
        for neighbor in tree[node]:
            if parents[neighbor] == 0:  # 아직 부모 노드가 설정되지 않은 이웃 노드인 경우
                parents[neighbor] = node  # 현재 노드를 이웃 노드의 부모로 설정
                stack.append(neighbor)  # 이웃 노드를 스택에 추가하여 나중에 방문
    
    return parents[2:]  # 2번 노드부터 마지막 노드까지의 부모 리스트를 반환

n = int(input())  # 노드의 개수
edges = [tuple(map(int, input().split())) for _ in range(n-1)]  # 간선 정보

result = find_parents(n, edges)  

for parent in result:
    print(parent)