👀 'Do it! 알고리즘 코딩테스트 with Python(김종관 저)'을 공부하고 정리한 내용입니다.

1. 개념

이진 트리는 각 노드의 자식 노드(차수)의 개수가 2 이하로 구성된 트리를 말합니다. 트리 영역에서 가장 많이 사용되는 형태입니다.

1-1. 이진트리의 종류

이진 트리에는 편향 이진 트리, 포화 이진 트리, 완전 이진 트리가 있습니다.

• 편향 이진 트리: 노드들이 한 쪽으로 편향되어 생성된 이진 트리
• 포화 이진 트리: 트리의 높이가 모두 일정하며 리프 노드가 꽊 찬 이진 트리
• 완전 이진 트리: 마지막 레벨을 제외하고 완전하게 노드들이 채워져 있고, 마지막 레벨은 왼쪽부터 채워진 트리

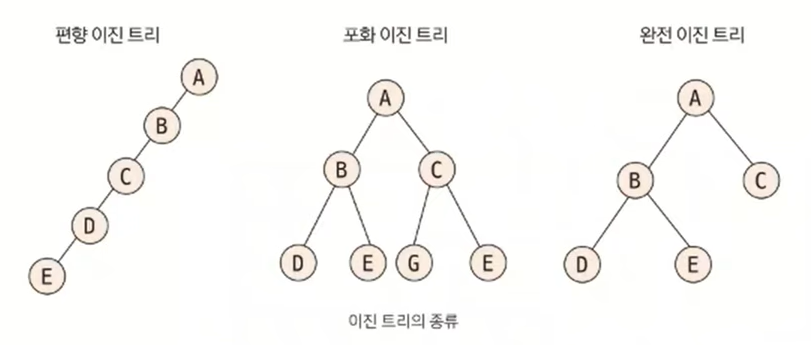
데이터를 트리 자료구조에 저장할 때 편향 이진 트리의 형태로 저장하면 탐색 속도가 저하되고 공간이 많이 낭비되는 단점이 있습니다. 일반적으로 코딩 테스트에서 데이터를 트리에 담는다고 하면 완전 이진 트리 형태를 떠올리면 됩니다.

1-2. 이진 트리의 순차 표현

가장 객관적이면서 편리한 트리 자료구조 형태틑 바로 '배열'입니다.

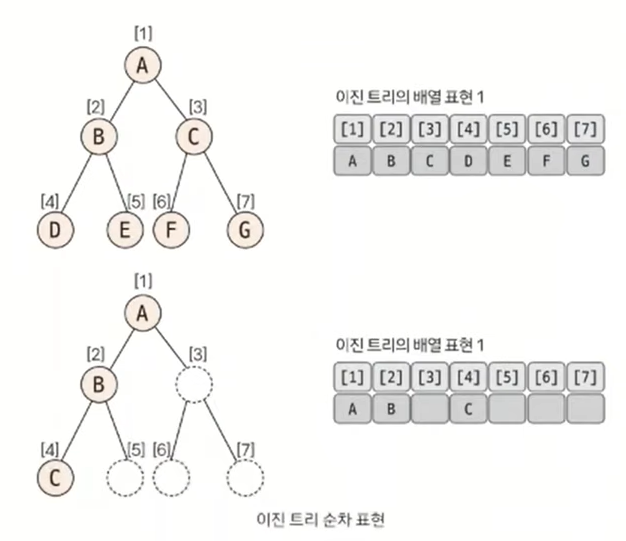
이진 트리는 위와 같이 1차원 배열의 형태로 표현할 수 있습니다. 그렇다면 이렇게 1차원 배열의 형태로 표현할 때 트리의 노드와 배열의 인덱스 간의 상관관계는 어떻게 될까요.

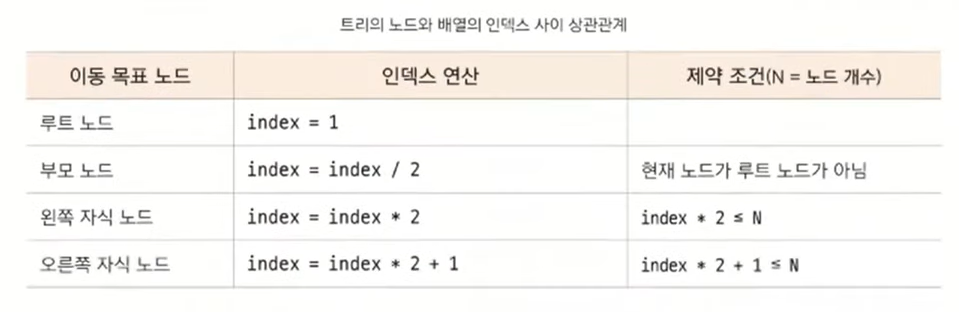
위의 인데스 연산 방식은 향후 세그먼트 트리나 LCA 알고리즘에서도 기본이 되는 연산이 됩니다.