해당 글은 제로베이스데이터스쿨 학습자료를 참고하여 작성되었습니다
딥러닝 쌩~으로 이해하기
학습절차

import numpy as np
X = np.array([
[0, 0, 1],
[0, 1, 1],
[1, 0, 1],
[1, 1, 1],
])활성화 함수의 종류

가중치 생성
# np.random.random의 range(0,1)이므로 -1~1로 만듦
W = 2 * np.random.random((1, 3)) - 1
w
---------------------------------------------------
array([[-0.69587368, 0.22372543, -0.26202276]])raw_weights로 추론
def Sigmoid(x):
return 1./(1. + np.exp(-x))
N = 4
for k in range(N):
x = X[k, :].T
v = np.matmul(W, x)
y = Sigmoid(v)
print(y)
----------------------------------------------
[0.43486653]
[0.49042684]
[0.27729956]
[0.3242801]가중치 업데이트 하기
X = np.array([ # features_data
[0, 0, 1],
[0, 1, 1],
[1, 0, 1],
[1, 1, 1],
])
D = np.array([[0], [0], [1], [1]]) # label_data필요 함수 정의
출력함수
def calc_output(W, x):
v = np.matmul(W, x)
y = Sigmoid(v)
return y오차 계산함수
# d : true_label_data
# y : pred_label_data
# d/dx(Sigmoid) = sig(1-sig)
def calc_error(d, y):
e = d - y
delta = y*(1-y) * e
return deltadW 계산함수
def delta_GD(W, X, D, alpha):
for k in range(4):
x = X[k, :].T
d = D[k]
y = calc_output(W, x)
delta = calc_error(d, y)
dW = alpha*delta*x
W = W + dW
return W모델학습
W = 2*np.random.random((1, 3)) - 1
alpha = 0.9
for epoch in range(10000):
W = delta_GD(W, X, D, alpha)
print(W)
---------------------------------------------------
[[ 0.26793891 -0.58857304 0.33312009]]
[[ 0.47429761 -0.55793964 0.32402775]]
[[ 0.65618083 -0.53973048 0.28925323]]
...
[[ 9.5650718 -0.2090675 -4.57477696]]
[[ 9.56517437 -0.20906715 -4.57482852]]
[[ 9.56527693 -0.2090668 -4.57488008]]학습결과
N = 4
print("Pred\t\tLabel")
for k in range(N):
x = X[k, :].T
v = np.matmul(W, x)
y = Sigmoid(v)
d = D[k]
print(f"{y}\t{d}")
----------------------------------------
Pred Label
[0.01020237] [0]
[0.00829357] [0]
[0.993243] [1]
[0.99168488] [1]XOR
raw_weigths 추론 결과
X = np.array([ # features_data
[0, 0, 1],
[0, 1, 1],
[1, 0, 1],
[1, 1, 1],
])
D = np.array([[0], [1], [1], [0]]) # label_data
W = 2*np.random.random((1,3)) - 1 # weights
# train
alpha = 0.9
for epoch in range(10000):
W = delta_GD(W, X, D, alpha)
# test
N = 4
print("Pred\t\tLabel")
for k in range(N):
x = X[k, :].T
v = np.matmul(W, x)
y = Sigmoid(v)
d = D[k]
print(f"{y}\t{d}")
---------------------------------------------------
Pred Label
[0.52965337] [0]
[0.5] [1]
[0.47034663] [1]
[0.44090112] [0]다시보는 딥러닝의 역사
초기 딥러닝은 XOR문제를 해결할 수 없어서 암흑기에 빠짐

XOR 극복을 하려면 다층신경망을 사용하면 된다는 것을 알고 있었으나,
다층 신경망에서 오차를 계산할 수 없었다

역전파
- 출력층부터 delta를 계산해서 은닉층으로 전달한다

딥러닝 모델 재구성 실시

Output 계산
def calc_output(W1, W2, x):
v1 = np.matmul(W1, x)
y1 = Sigmoid(v1)
v = np.matmul(W2, y1)
y = Sigmoid(v)
return y, y1출력층의 델타 계산
def calc_delta(d, y):
e = d - y
delta = y*(1-y)*e
return delta은닉층의 델타 계산

def calc_delta1(W2, delta, y1):
e1 = np.matmul(W2.T, delta)
delta1 = y1*(1-y1) * e1
return delta1활성화 함수들의 미분값

역전파
def backprop_XOR(W1, W2, X, D, alpha):
for k in range(4):
x = X[k, :].T
d = D[k]
y, y1 = calc_output(W1, W2, x)
delta = calc_delta(d, y)
delta1 = calc_delta1(W2, delta, y1)
dW1 = (alpha*delta1).reshape(4, 1) * x.reshape(1, 3)
W1 = W1 + dW1
dW2 = alpha * delta * y1
W2 = W2 + dW2
return W1, W2역전파 모델 생성
# features_data
X = np.array([
[0, 0, 1],
[0, 1, 1],
[1, 0, 1],
[1, 1, 1],
])
# label_data
D = np.array([[0], [1], [1], [0]])
# weights
W1 = 2*np.random.random((4, 3)) - 1
W2 = 2*np.random.random((1, 4)) - 1
# train
alpha = 0.9
for epoch in range(10000):
W1, W2 = backprop_XOR(W1, W2, X, D, alpha)
# test
N = 4
print("Pred\t\tLabel")
for k in range(N):
x = X[k, :].T
v1 = np.matmul(W1, x)
y1 = Sigmoid(v1)
v = np.matmul(W2, y1)
y = Sigmoid(v)
d = D[k]
print(f"{y}\t{d}")
--------------------------------------------------------
Pred Label
[0.00756898] [0]
[0.98994333] [1]
[0.98986829] [1]
[0.01421657] [0]CrossEntropy Loss

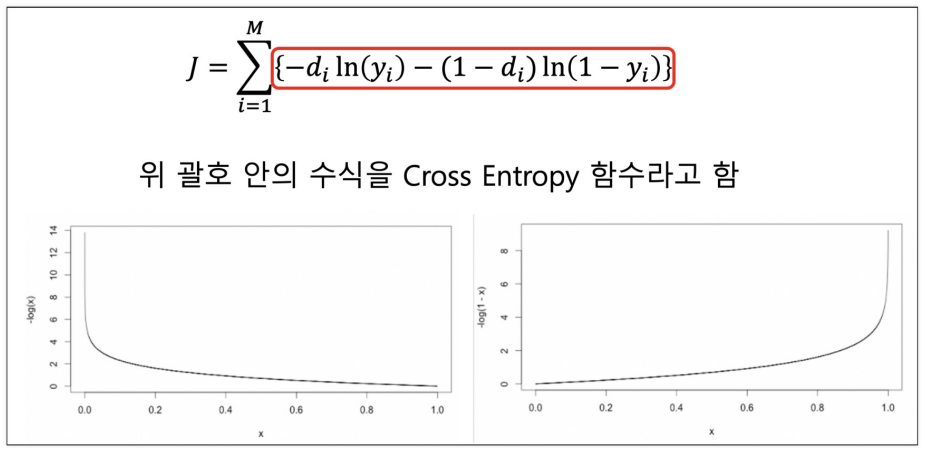
필요 함수 정의
def calcDelta_ce(d, y):
e = d - y
delta = e
return delta
def calcDelta1_ce(W2, delta, y1):
e1 = np.matmul(W2.T, delta)
delta1 = y1*(1-y1) * e1
return delta1
def BackpropCE(W1, W2, X, D, alpha):
for k in range(4):
x = X[k, :].T
d = D[k]
y, y1 = calc_output(W1, W2, x)
delta = calcDelta_ce(d, y)
delta1 = calcDelta1_ce(W2, delta, y1)
dW1 = (alpha*delta1).reshape(4, 1) * x.reshape(1, 3)
W1 = W1 + dW1
dW2 = alpha * delta * y1
W2 = W2 + dW2
return W1, W2역전파, loss=cross_entropy 모델학습
# features
X = np.array([
[0, 0, 1],
[0, 1, 1],
[1, 0, 1],
[1, 1, 1],
])
# label
D = np.array([[0], [1], [1], [0]])
# weights
W1 = 2*np.random.random((4, 3)) - 1
W2 = 2*np.random.random((1, 4)) - 1
# train
for epoch in range(5000):
W1, W2 = BackpropCE(W1, W2, X, D, alpha=0.9)
# test
N = 4
print("Pred\t\tLabel")
for k in range(N):
x = X[k, :].T
v1 = np.matmul(W1, x)
y1 = Sigmoid(v1)
v = np.matmul(W2, y1)
y = Sigmoid(v)
d = D[k]
print(f"{y}\t{d}")
-------------------------------------------------------
Pred Label
[7.64196953e-05] [0]
[0.99932061] [1]
[0.99976409] [1]
[0.00106609] [0]2. 숫자맞추기

import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm
%matplotlib inlineSoftmax
def Softmax(x):
x = np.subtract(x, np.max(x)) # prevent overflow
ex = np.exp(x)
return ex / np.sum(ex)Train data
X = np.zeros((5,5,5))
X[:, :, 0] = [
[0,1,1,0,0],
[0,0,1,0,0],
[0,0,1,0,0],
[0,0,1,0,0],
[0,1,1,1,0] ]
X[:, :, 1] = [
[1,1,1,1,0],
[0,0,0,0,1],
[0,1,1,1,0],
[1,0,0,0,0],
[1,1,1,1,1] ]
X[:, :, 2] = [
[1,1,1,1,0],
[0,0,0,0,1],
[0,1,1,1,0],
[0,0,0,0,1],
[1,1,1,1,0] ]
X[:, :, 3] = [
[0,0,0,1,0],
[0,0,1,1,0],
[0,1,0,1,0],
[1,1,1,1,1],
[0,0,0,1,0] ]
X[:, :, 4] = [
[1,1,1,1,1],
[1,0,0,0,0],
[1,1,1,1,0],
[0,0,0,0,1],
[1,1,1,1,0] ]
D = np.array([
[[1,0,0,0,0]],
[[0,1,0,0,0]],
[[0,0,1,0,0]],
[[0,0,0,1,0]],
[[0,0,0,0,1]],
])
plt.figure(figsize=(12, 4))
for n in range(5):
plt.subplot(1, 5, n+1)
plt.imshow(X[:,:,n])
plt.show()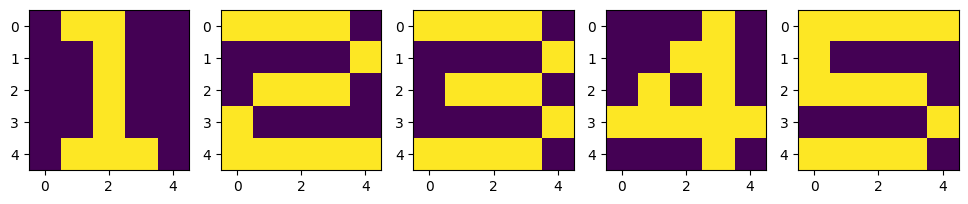
ReLU

def ReLU(x):
return np.maximum(0,x)Forward()
def calcOutput_ReLU(W1, W2, W3, W4, x):
v1 = np.matmul(W1, x)
y1 = ReLU(v1)
v2 = np.matmul(W2, y1)
y2 = ReLU(v2)
v3 = np.matmul(W3, y2)
y3 = ReLU(v3)
v = np.matmul(W4, y3)
y = Softmax(v)
return y, v1, v2, v3, y1, y2, y3Backward()
def backpropagation_ReLU(d, y, W2, W3, W4, v1, v2, v3):
e = d - y
delta = e
e3 = np.matmul(W4.T, delta)
delta3 = (v3 > 0) * e3
e2 = np.matmul(W3.T, delta3)
delta2 = (v2 > 0) * e2
e1 = np.matmul(W2.T, delta2)
delta1 = (v1 > 0) * e1
return delta, delta1, delta2, delta3가중치 계산
def calcWs(alpha, delta, delta1, delta2, delta3, y1, y2, y3, x, W1, W2, W3, W4):
dW4 = alpha * delta * y3.T
W4 = W4 + dW4
dW3 = alpha * delta3 * y2.T
W3 = W3 + dW3
dW2 = alpha * delta2 * y1.T
W2 = W2 + dW2
dW1 = alpha * delta1 * x.T
W1 = W1 + dW1
return W1, W2, W3, W4가중치 업데이트
def DeepReLU(W1, W2, W3, W4, X, D, alpha):
for k in range(5):
x = np.reshape(X[:, :, k], (25, 1))
d = D[k, :].T
y, v1, v2, v3, y1, y2, y3 = calcOutput_ReLU(W1, W2, W3, W4, x)
delta, delta1, delta2, delta3 = backpropagation_ReLU(d, y, W2, W3, W4, v1, v2, v3)
W1, W2, W3, W4 = calcWs(alpha, delta, delta1, delta2, delta3, y1, y2, y3, x, W1, W2, W3, W4)
return W1, W2, W3, W4모델 학습
W1 = 2*np.random.random((20, 25))-1
W2 = 2*np.random.random((20, 20))-1
W3 = 2*np.random.random((20, 20))-1
W4 = 2*np.random.random((5, 20))-1
alpha = 0.01
for epoch in tqdm(range(10000)):
W1, W2, W3, W4 = DeepReLU(W1, W2, W3, W4, X, D, alpha)
---------------------------------------------------------------
100%|██████████| 10000/10000 [00:04<00:00, 2103.66it/s]훈련데이터 검증
def verify_algorithm(x, W1, W2, W3, W4):
v1 = np.matmul(W1, x)
y1 = ReLU(v1)
v2 = np.matmul(W2, y1)
y2 = ReLU(v2)
v3 = np.matmul(W3, y2)
y3 = ReLU(v3)
v = np.matmul(W4, y3)
y = Softmax(v)
return y
N = 5
for k in range(N):
x = np.reshape(X[:, :, k], (25,1))
y = verify_algorithm(x, W1, W2, W3, W4)
print("Y={}:".format(k+1))
print(np.argmax(y, axis=0)+1)
print(y)
print("-"*30)
--------------------------------------------------------------
Y=1:
[1]
[[9.99985781e-01]
[3.29453652e-07]
[8.55703081e-06]
[5.26350210e-06]
[6.91014050e-08]]
------------------------------
Y=2:
[2]
[[4.52457064e-07]
[9.99955743e-01]
[1.01007071e-06]
[1.10620990e-05]
[3.17318761e-05]]
------------------------------
Y=3:
[3]
[[6.32634142e-06]
[8.85408903e-06]
[9.99971751e-01]
[8.76826674e-09]
[1.30593499e-05]]
------------------------------
Y=4:
[4]
[[1.22508750e-05]
[6.70278920e-06]
[5.40146785e-17]
[9.99981046e-01]
[7.87918309e-17]]
------------------------------
Y=5:
[5]
[[2.90763346e-06]
[1.54421358e-05]
[1.50301397e-05]
[1.36885820e-07]
[9.99966483e-01]]
------------------------------Test data
X_test = np.zeros((5,5,5))
X_test[:, :, 0] = [
[0,0,0,0,0],
[0,1,0,0,0],
[1,0,1,0,0],
[0,0,1,0,0],
[0,1,1,1,0],
]
X_test[:, :, 1] = [
[1,1,1,1,0],
[0,0,0,0,0],
[0,1,1,1,0],
[0,0,0,0,1],
[1,1,1,1,0], ]
X_test[:, :, 2] = [
[0,0,0,1,0],
[0,0,1,1,0],
[0,1,0,0,0],
[1,1,1,0,1],
[0,0,0,1,0], ]
X_test[:, :, 3] = [
[1,1,1,1,0],
[0,0,0,0,1],
[0,1,1,1,0],
[1,0,0,0,0],
[1,1,1,0,0], ]
X_test[:, :, 4] = [
[0,1,1,1,1],
[1,1,0,0,0],
[1,1,1,1,0],
[0,0,0,1,1],
[1,1,1,1,0], ]
plt.figure(figsize=(12, 4))
for n in range(5):
plt.subplot(1, 5, n+1)
plt.imshow(X_test[:,:,n])
plt.show()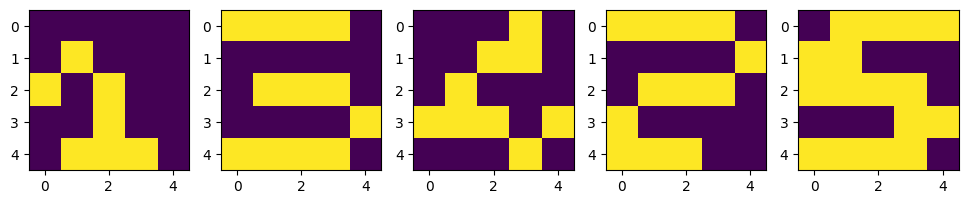
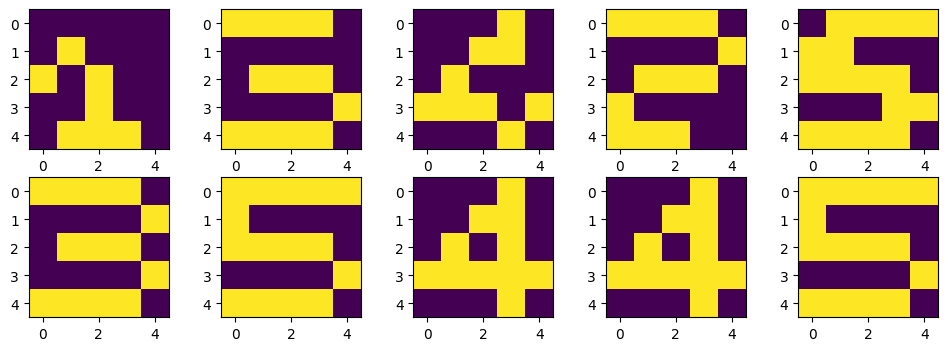
검증
learning_result=[0,0,0,0,0]
N = 5
for k in range(N):
x = np.reshape(X_test[:, :, k], (25,1))
y = verify_algorithm(x, W1, W2, W3, W4)
learning_result[k] = np.argmax(y, axis=0)+1
plt.figure(figsize=(12, 4))
for n in range(5):
plt.subplot(2, 5, n+1)
plt.imshow(X_test[:,:,n])
plt.subplot(2, 5, n+6)
plt.imshow(X[:,:, learning_result[n][0]-1])
plt.show()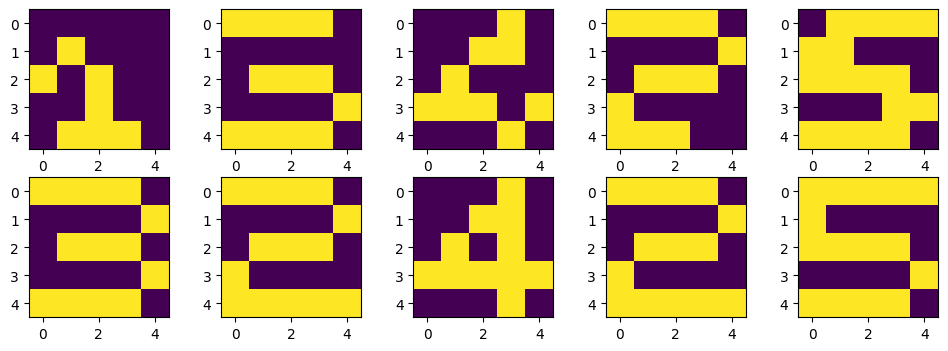
dropout
- 과적합을 방지하기 위해 뉴런 일부를 사용하지 않는 것
- 학습할 때만 사용하고, 검증/평가에는 사용하지 않음
dropout 함수
def Dropout(y, ratio):
ym = np.zeros_like(y)
num = round(y.size*(1-ratio))
idx = np.random.choice(y.size, num, replace=False)
ym[idx] = 1./(1.-ratio)
return ym출력함수
def calcOutput_Dropout(W1, W2, W3, W4, x):
v1 = np.matmul(W1, x)
y1 = Sigmoid(v1)
y1 = y1 * Dropout(y1, 0.2)
v2 = np.matmul(W2, y1)
y2 = Sigmoid(v2)
y2 = y2 * Dropout(y2, 0.2)
v3 = np.matmul(W3, y2)
y3 = Sigmoid(v3)
y3 = y3 * Dropout(y3, 0.2)
v = np.matmul(W4, y3)
y = Softmax(v)
return y, y1, y2, y3, v1, v2, v3역전파 함수
def backpropagation_Dropout(d, y, y1, y2, y3, W2, W3, W4, v1, v2, v3):
e = d - y
delta = e
e3 = np.matmul(W4.T, delta)
delta3 = y3*(1-y3) * e3
e2 = np.matmul(W3.T, delta3)
delta2 = y2*(1-y2) * e2
e1 = np.matmul(W2.T, delta2)
delta1 = y1*(1-y1) * e1
return delta, delta1, delta2, delta3모델 실행
def DeepDropout(W1, W2, W3, W4, X, D):
for k in range(5):
x = np.reshape(X[:, :, k], (25, 1))
d = D[k, :].T
y, y1, y2, y3, v1, v2, v3 = calcOutput_Dropout(W1, W2, W3, W4, x)
delta, delta1, delta2, delta3 = backpropagation_Dropout(d, y, y1, y2, y3, W2, W3, W4, v1, v2, v3)
W1, W2, W3, W4 = calcWs(alpha, delta, delta1, delta2, delta3, y1, y2, y3, x, W1, W2, W3, W4)
return W1, W2, W3, W4W1 = 2*np.random.random((20, 25))-1
W2 = 2*np.random.random((20, 20))-1
W3 = 2*np.random.random((20, 20))-1
W4 = 2*np.random.random((5, 20))-1
for epoch in tqdm(range(10000)):
W1, W2, W3, W4 = DeepDropout(W1, W2, W3, W4, X, D)모델평가
def verify_algorithm(x, W1, W2, W3, W4):
v1 = np.matmul(W1, x)
y1 = Sigmoid(v1)
v2 = np.matmul(W2, y1)
y2 = Sigmoid(v2)
v3 = np.matmul(W3, y2)
y3 = Sigmoid(v3)
v = np.matmul(W4, y3)
y = Softmax(v)
return yN = 5
for k in range(N):
x = np.reshape(X_test[:, :, k], (25,1))
y = verify_algorithm(x, W1, W2, W3, W4)
learning_result[k] = np.argmax(y, axis=0)+1
plt.figure(figsize=(12, 4))
for n in range(5):
plt.subplot(2, 5, n+1)
plt.imshow(X_test[:,:,n])
plt.subplot(2, 5, n+6)
plt.imshow(X[:,:, learning_result[n][0]-1])
plt.show()