해당 글은 제로베이스데이터스쿨 학습자료를 참고하여 작성되었습니다

1. 회귀(Regression)

• 머신러닝에서 회귀는 특성과 라벨 데이터로 학습 후 예측하는 것
  

예시) 보스턴 집 값 예측

• 단순선형회귀로 가정한다면, 특성 1개에 라벨1개(1차식)
  

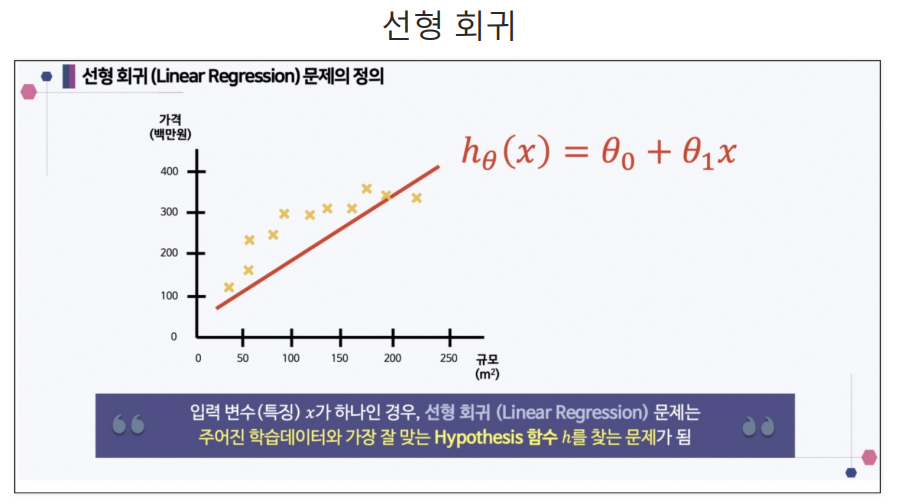
OLS : Ordinary Linear Least Square(=최소자승법, 잔차제곱법(RSS))

• 잔차를 제곱하여 최적의 파라미터를 찾는 방법

• 제곱하는 이유 : 오차가 큰 경우 더 큰 값을 갖게하여 파라미터가 변동 폭이 적은 쪽으로 도출하게 됨

잔차(Residue)

• 평균이 0인 정규분포를 따르는 것이어야 함

• $e\ =\ y\ -\ \hat{y}$

• 오차 : 모집단의 회귀식에 대한 편차값

• 잔차 : 표본집단의 회귀식에 대한 편차값

즉, 오차는 관측값을 통해 예측한 가정이 실제와 얼마나 부합하는지의 정도를 말해준다면 잔차는 예측한 가정이 관측값을 얼마나 잘 반영하고 있는가를 의미한다고 할 수 있다.

예시

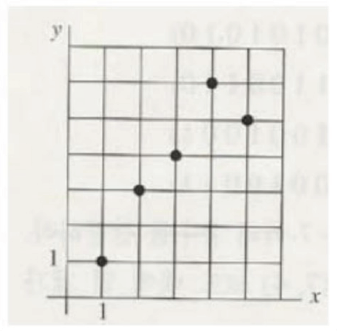
import pandas as pd

data = { 'x' : [1., 2., 3., 4., 5.],
        'y':[1., 3., 4., 6., 5.,]}
df = pd.DataFrame(data)
df
--------------------
     x    y
0  1.0  1.0
1  2.0  3.0
2  3.0  4.0
3  4.0  6.0
4  5.0  5.0

OLS를 활용한 모델생성

• "y ~ x"는 x를 변수로 갖는 식 y 라는 의미

import statsmodels.formula.api as smf

lm_model = smf.ols(formula="y ~ x", data=df).fit()

파라미터 확인

lm_model.params
# y = 1.1x + 0.5
-----------------
Intercept    0.5
x            1.1
dtype: float64

시각화

import matplotlib.pyplot as plt
import seaborn as sns

plt.figure(figsize=(12, 7))
sns.lmplot(data=df, x='x', y='y')
plt.grid()
plt.xlim([0, 5])
plt.show()

잔차 확인

resid = lm_model.resid
resid
--------------
0   -0.6
1    0.3
2    0.2
3    1.1
4   -1.0
dtype: float64

잔차분포도

sns.distplot(resid)

결정계수 R-Sqaured

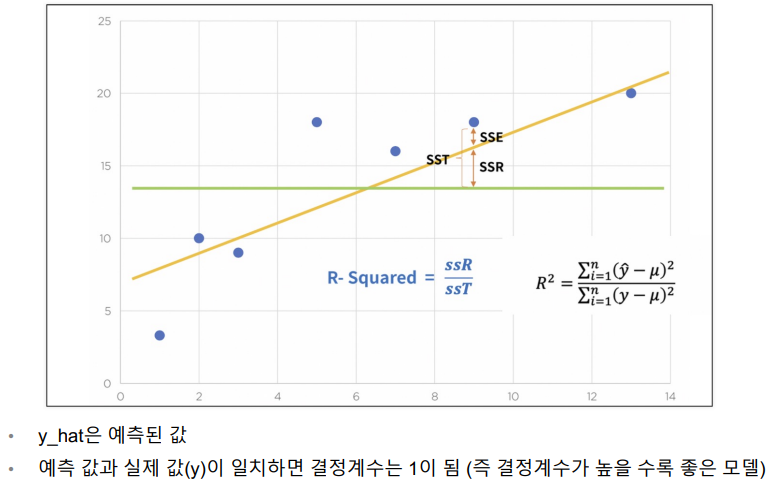
R-Squared 계산하기

• 분모 : (참값 - 평균값)^2의 합
• 분자 : (예측값 - 평균값)^2의 합

import numpy as np

mu = np.mean(df['y'])
y = df['y']

y_hat = lm_model.predict()
np.sum( (y_hat - mu)**2) / np.sum( (y-mu)**2 )
----------------------------------------------
0.8175675675675674

R-Squared 계수 확인

lm_model.rsquared

---

2. e-커머스 데이터

e-커머스 데이터 가져오기

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

data_url = 'https://raw.githubusercontent.com/PinkWink/ML_tutorial/master/dataset/ecommerce.csv'
data = pd.read_csv(data_url)
data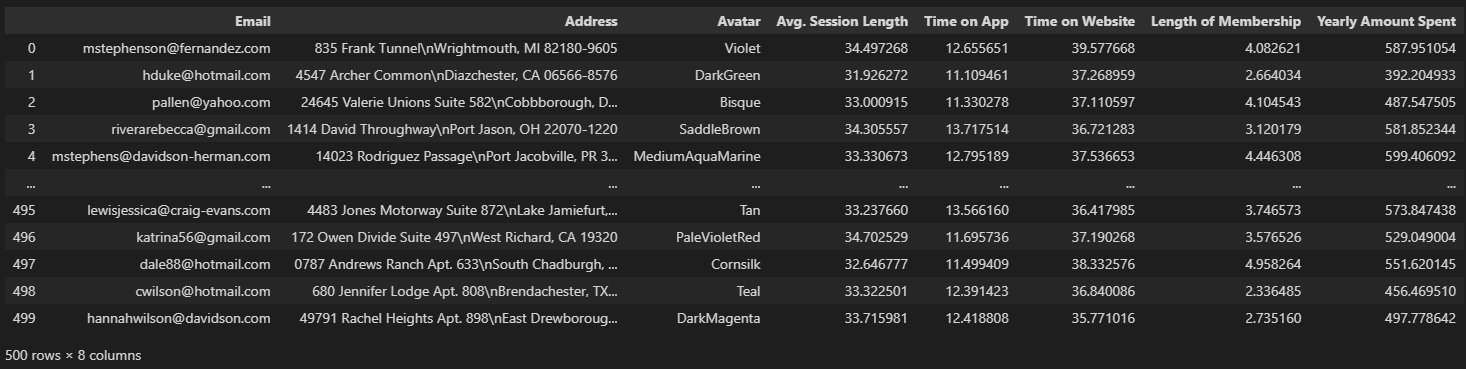

데이터 이해하기

• Avg. Session Length : 한 번 접속했을 때 평균 어느 정도의 시간을 사용하는지에 대한 데이터
• Time on App : 폰 앱으로 접속했을 때 유지 시간 (분)
• Time on Website : 웹사이트로 접속했을 때 유지 시간 (분)
• Length of Membership : 회원 자격 유지 기간 (연)

불필요 칼럼 삭제

• 라벨 : Yearly Amount Spent(연간지출액)

data.drop(['Email', 'Address', 'Avatar'], axis=1, inplace=True)
data.info()
--------------------------------------------------
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 500 entries, 0 to 499
Data columns (total 5 columns):
 #   Column                Non-Null Count  Dtype  
---  ------                --------------  -----  
 0   Avg. Session Length   500 non-null    float64
 1   Time on App           500 non-null    float64
 2   Time on Website       500 non-null    float64
 3   Length of Membership  500 non-null    float64
 4   Yearly Amount Spent   500 non-null    float64
dtypes: float64(5)
memory usage: 19.7 KB

boxplot

fig, ax = plt.subplots(2, 1, figsize=(12, 6))

sns.boxplot(data=data.iloc[:, :-1], ax=ax[0]);
ax[0].set_title('Features')
ax[0].grid()

sns.boxplot(data=data['Yearly Amount Spent'], ax=ax[1]);
ax[1].set_title('Label')
ax[1].grid()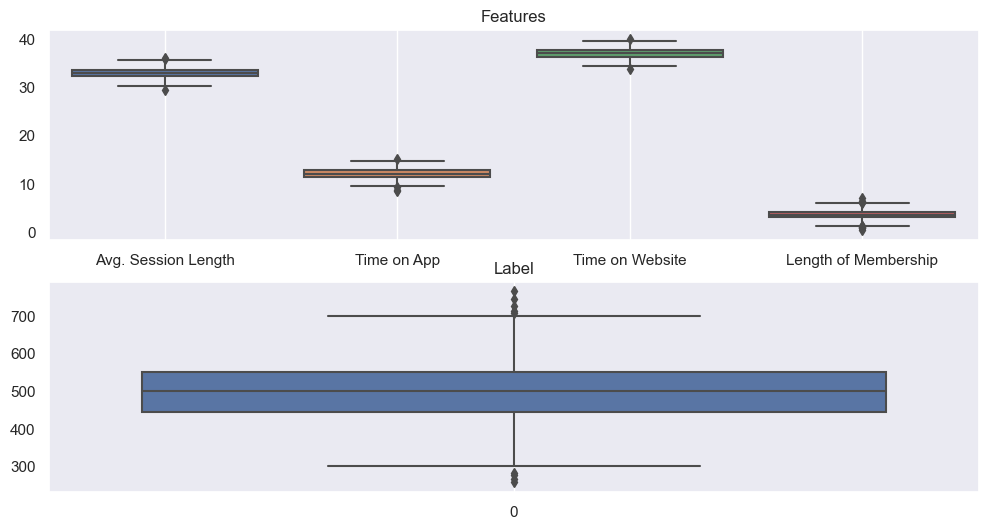

전체경향 확인

• 'Yearly Amount Spent'와 관계가 있는 것은 'Length of Membership'이다

sns.pairplot(data=data);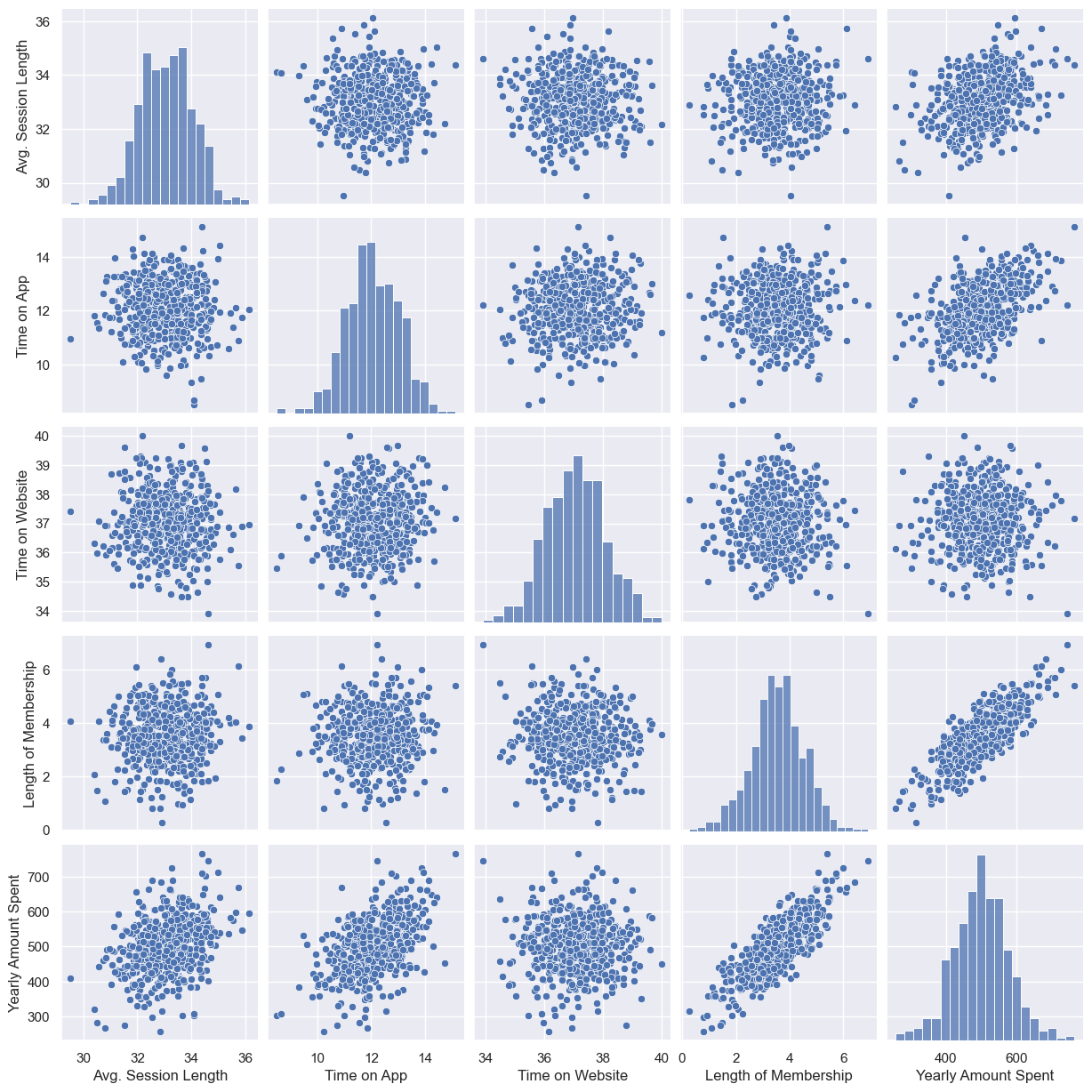

연간비용과 멤버쉽 유지기간 간의 시각화

sns.lmplot(data=data, x="Length of Membership", y="Yearly Amount Spent");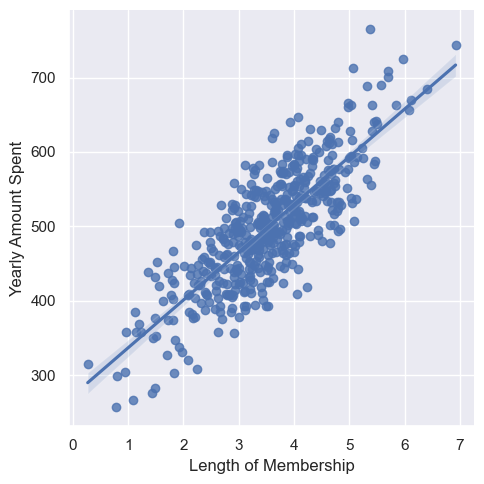

OLS 학습 결과

• 연간비용과 멤버쉽만 활용
• R-Squared : 모형 적합도
• Adj. R-Squared : 독립변수가 여러 개인 다중회귀분석에서 사용
• Prob. F-Statistic : 회귀무형에 대한 통계적 유의미성 검정.
• 이 값이 0.05 이하라면 모집단에서도 의미가 있다고 볼 수 있음

import statsmodels.api as sm

X = data['Length of Membership']
y = data['Yearly Amount Spent']

X = np.c_[X, [1]*len(X)] # 상수항(b)와 곱해질 1을 가진 열 추가

# 주의 : 라벨데이터가 선순위, 특성데이터가 후순위
lm = sm.OLS(y, X).fit()
lm.summary()

회귀모델 그리기

pred = lm.predict(X)

plt.figure(figsize=(12, 6))
sns.scatterplot(x=X[:, 0], y=y)
plt.plot(X[:, 0], pred, '--r', lw=2);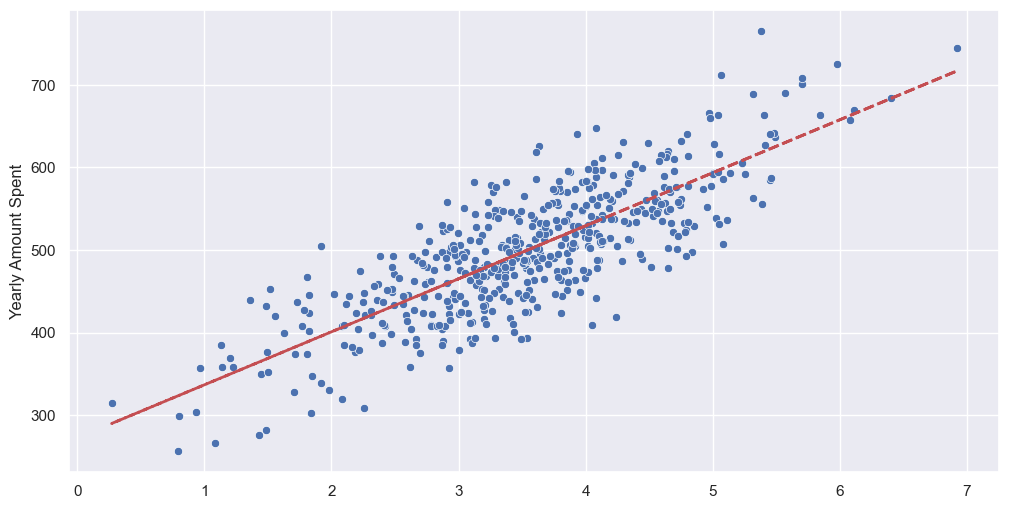

참값 vs 예측값

sns.scatterplot(x=y, y=pred)
plt.plot([min(y), max(y)], [min(y), max(y)], '--r', lw=3);

전체데이터로 회귀

from sklearn.model_selection import train_test_split

X = data.drop('Yearly Amount Spent', axis=1)
y = data['Yearly Amount Spent']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=13)

import statsmodels.api as sm

lm = sm.OLS(y_train, X_train).fit()
lm.summary()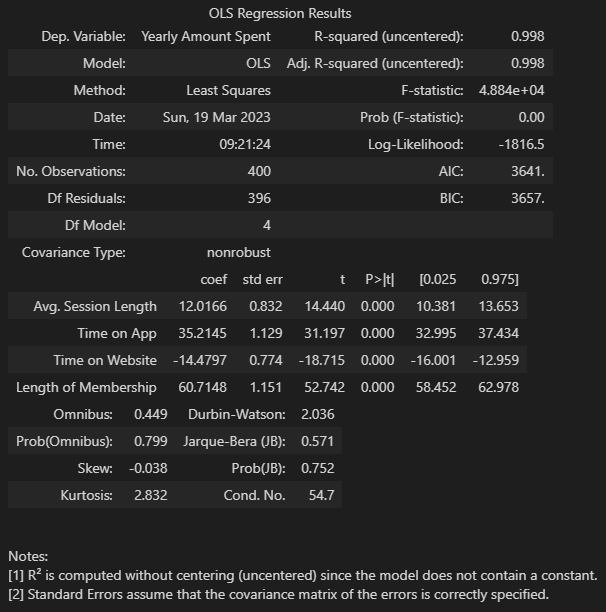

참값 vs 예측값

pred = lm.predict(X)

sns.scatterplot(x=y_test, y=pred)
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], '--r', lw=3);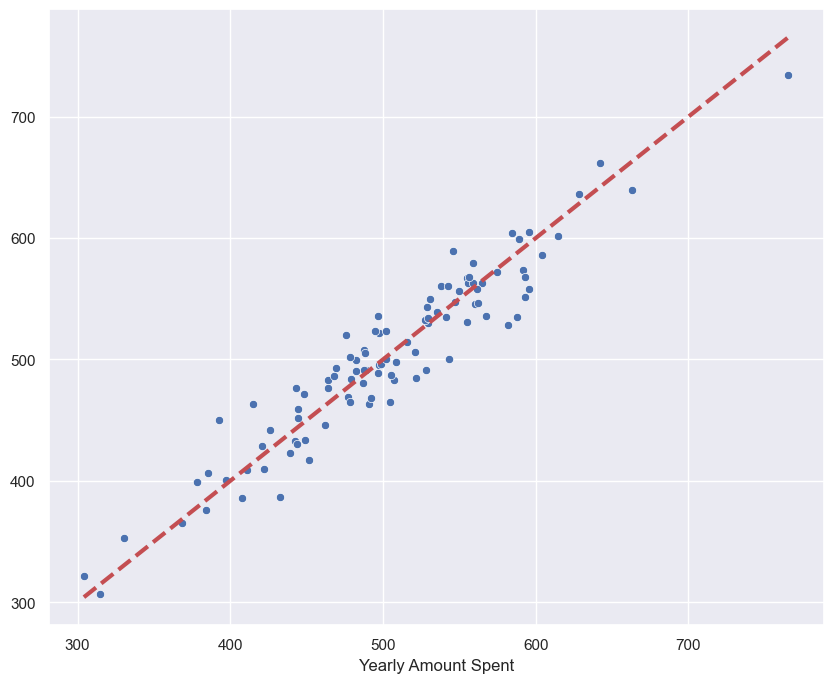

---

3. 비용함수(Cost Function)

• 원래의 값과 가장 오차가 작은 최적의 가중치를 도출하는 함수

선형회귀

아래와 같이 데이터가 있을 때, 이에 최적인 회귀선을 생성할 때 사용한다

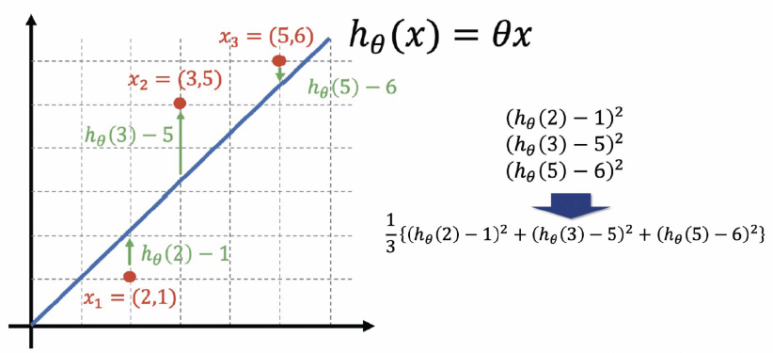
이 식을 비용함수(Cost Function)이고, 손실을 최소화 하는 파라미터를 찾을 수 있다.

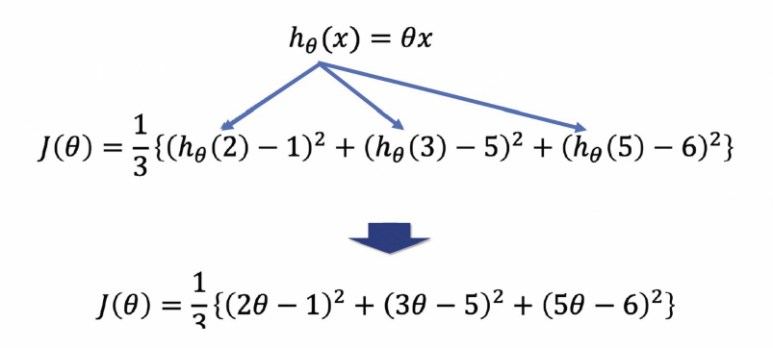
파이썬 활용

import numpy as np

coff = np.poly1d([2, -1])**2 + np.poly1d([3, -5])**2 + np.poly1d([5, -6])**2
coff
-----------------------
poly1d([ 38, -94,  62])

곡선 생성

x = np.linspace(-3, 6, 1000)
y = coff[2]*x**2 + coff[1]*x + coff[0]

plt.plot(x, y, label=f'${coff[2]}\u03b8^2 + {coff[1]}\u03b8 + {coff[0]}$'.replace('+ -', '-'));
plt.legend()
plt.grid()

계수 구하기

import sympy as sym

th = sym.Symbol('th')
diff_th = sym.diff(coff[2]*th**2 + coff[1]*th + coff[0], th)
diff_th
------------------------
76*th - 94

th = 94/76
th
-------------------
1.236842105263158

회귀선 그리기

x1 = [2, 3, 5]
y1 = [1, 5, 6]
x2 = np.linspace(0, 6, 100)
y2 = th * x2

plt.scatter(x1, y1, c='r')
plt.plot(x2, y2, label='')
plt.grid()

경사하강법

• 실제 데이터들은 복잡하여 위의 방식을 적용하기 어렵다.

• 손실함수를 최소화시키는 방법

1) 임의의 위치 선정

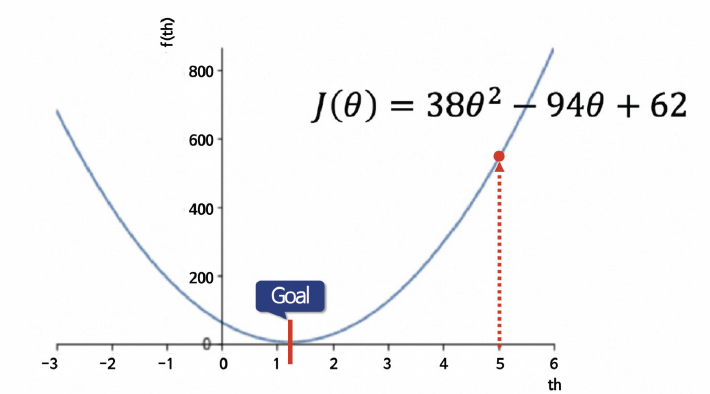
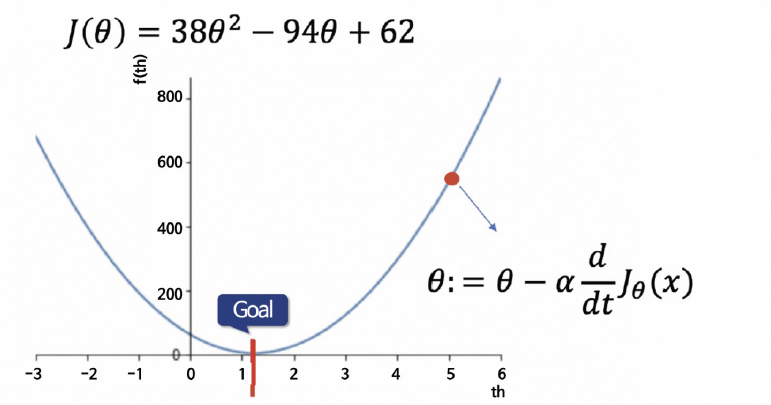
2) 임의의 점에서 미분값을 계산해서 업데이트

• 이 과정을 반복하여 목표에 도달
• 좌측에서 점을 잡아도 목표로 이동
  

---

4. 보스턴 집값 예측

개요

• 여러 칼럼들로 보스턴의 집값 데이터가 존재한다
• 이를 활용하여 집값을 예측해보자

목표

• 선형회귀로 집값 예측

절차

• 1) 데이터 이해
• 2) 선형회귀 적용
• 3) LSTAT 칼럼을 제거한 선형회귀

1) 데이터이해

데이터가져오기

• 버전이 상승하면서 datasets에서 boston 데이터가 삭제되었다
• fetch_openml을 활용해야하며, version=1로 사용해야한다
• verison=2는 PRICE데이터가 숫자형이 아니다

from sklearn.datasets import fetch_openml
import pandas as pd

X, y = fetch_openml('boston', return_X_y=True, parser='auto', version=1)
boston_pd = X
boston_pd['PRICE'] = y
boston_pd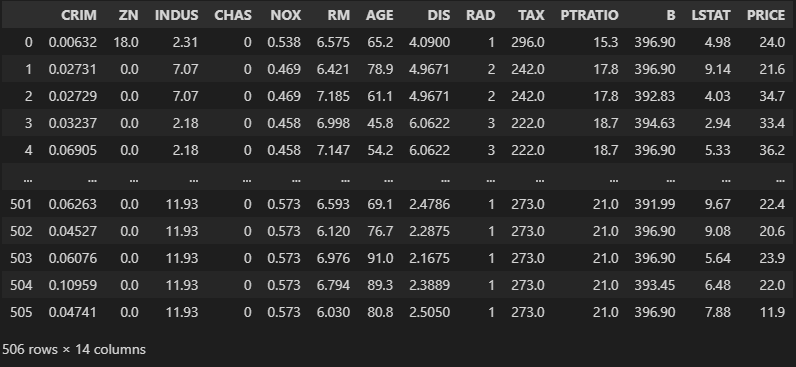

칼럼정보

오류

TypeError: can't multiply sequence by non-int of type 'float'

데이터 타입이 잘못된 경우이다.
선형회귀 수행 시 데이터 타입이 숫자형(int, float)이어야 하는데,
CHAS와 RAD가 눈으로 보기에 정수형이지만 info()를 확인한 결과,
category형이었다. 이를 다른 데이터와 같은 float형으로 변환했다

데이터형 변환

boston_pd.info()
--------------------------------------
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 506 entries, 0 to 505
Data columns (total 14 columns):
 #   Column   Non-Null Count  Dtype   
---  ------   --------------  -----   
 0   CRIM     506 non-null    float64 
 1   ZN       506 non-null    float64 
 2   INDUS    506 non-null    float64 
 3   CHAS     506 non-null    category
 4   NOX      506 non-null    float64 
 5   RM       506 non-null    float64 
 6   AGE      506 non-null    float64 
 7   DIS      506 non-null    float64 
 8   RAD      506 non-null    category
 9   TAX      506 non-null    float64 
 10  PTRATIO  506 non-null    float64 
 11  B        506 non-null    float64 
 12  LSTAT    506 non-null    float64 
 13  PRICE    506 non-null    float64 
dtypes: category(2), float64(12)
memory usage: 49.0 KB

boston_pd['CHAS'] = boston_pd['CHAS'].astype('float64')
boston_pd['RAD'] = boston_pd['RAD'].astype('float64')
boston_pd.info()
----------------------------------------
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 506 entries, 0 to 505
Data columns (total 14 columns):
 #   Column   Non-Null Count  Dtype  
---  ------   --------------  -----  
 0   CRIM     506 non-null    float64
 1   ZN       506 non-null    float64
 2   INDUS    506 non-null    float64
 3   CHAS     506 non-null    float64
 4   NOX      506 non-null    float64
 5   RM       506 non-null    float64
 6   AGE      506 non-null    float64
 7   DIS      506 non-null    float64
 8   RAD      506 non-null    float64
 9   TAX      506 non-null    float64
 10  PTRATIO  506 non-null    float64
 11  B        506 non-null    float64
 12  LSTAT    506 non-null    float64
 13  PRICE    506 non-null    float64
dtypes: float64(14)
memory usage: 55.5 KB

Label 데이터 확인

import plotly.express as px

fig = px.histogram(boston_pd, x="PRICE")
fig.show()

상관관계 확인

• 주요 상관관계 : RM(방 갯수), LSTAT(저소득층 인구)

import matplotlib.pyplot as plt
import seaborn as sns

corr_mat = boston_pd.corr().round(1)
sns.set(rc={'figure.figsize':(10,8)})
sns.heatmap(data=corr_mat, annot=True, cmap='bwr');

주요상관관계 시각화

• 가격은 저소득층인구에 반비례, 방 갯수에 비례
• 저소득층 인구는 소득이 적은 사람을 의미하는데 이는 PRICE의 다른 형태가 아닌가??

fig, ax = plt.subplots(1, 2)
sns.regplot(x='RM', y='PRICE', data=boston_pd, ax=ax[0])
sns.regplot(x='LSTAT', y='PRICE', data=boston_pd, ax=ax[1])
plt.show()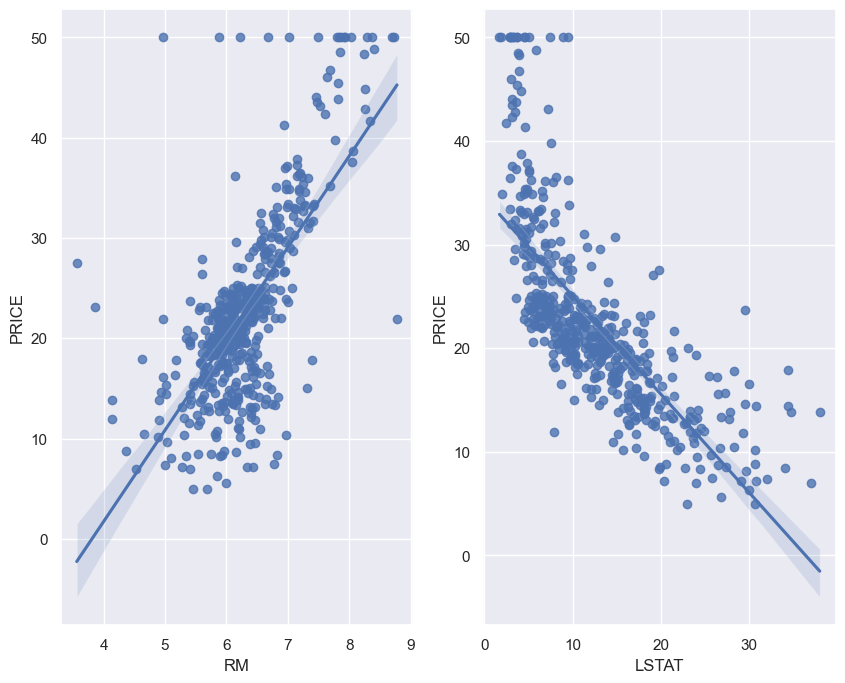

2) LSTAT를 포함한 선형회귀

import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

X = boston_pd.drop('PRICE', axis=1)
y = boston_pd['PRICE']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=13)

reg = LinearRegression()
reg.fit(X_train, y_train)

pred_tr = reg.predict(X_train)
pred_test = reg.predict(X_test)
rmse_tr = np.sqrt(mean_squared_error(y_train, pred_tr))
rmse_test = np.sqrt(mean_squared_error(y_test, pred_test))

print('RMSE of Train Data : ', rmse_tr)
print('RMSE of Test Data : ', rmse_test)
----------------------------------------
RMSE of Train Data :  4.642806069019824
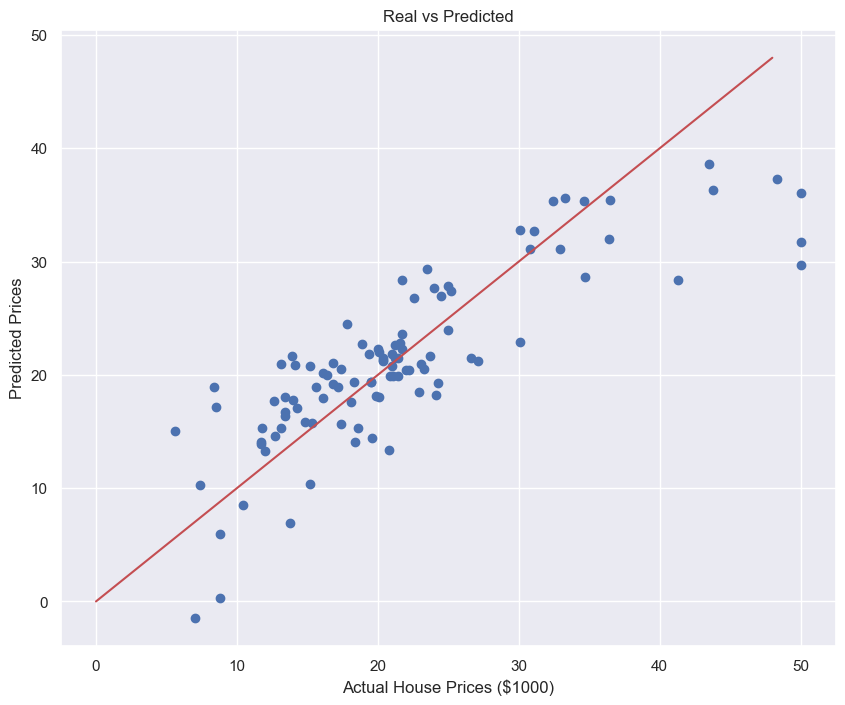
RMSE of Test Data :  4.931352584146711

성능확인 시각화

plt.scatter(y_test, pred_test)
plt.xlabel("Actual House Prices ($1000)")
plt.ylabel("Predicted Prices")
plt.title("Real vs Predicted")
plt.plot([0,48],[0,48],'r')
plt.show()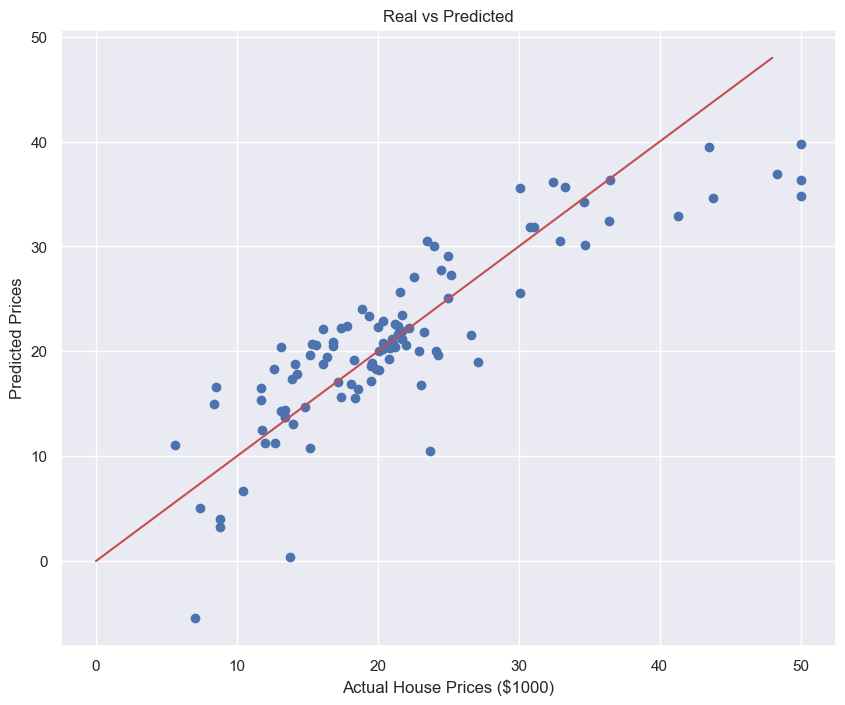

3) LSTAT를 제거한 선형회귀

• 오차가 더 증가한다. 이런 것을 포함해야 할지 말지는 엔지니어의 몫이다.

X = boston_pd.drop(['PRICE','LSTAT'], axis=1)
y = boston_pd['PRICE']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=13)

reg = LinearRegression()
reg.fit(X_train, y_train)

pred_tr = reg.predict(X_train)
pred_test = reg.predict(X_test)
rmse_tr = np.sqrt(mean_squared_error(y_train, pred_tr))
rmse_test = np.sqrt(mean_squared_error(y_test, pred_test))

print('RMSE of Train Data : ', rmse_tr)
print('RMSE of Test Data : ', rmse_test)
----------------------------------------
RMSE of Train Data :  5.165137874244864
RMSE of Test Data :  5.295595032597162

성능확인 시각화

plt.scatter(y_test, pred_test)
plt.xlabel("Actual House Prices ($1000)")
plt.ylabel("Predicted Prices")
plt.title("Real vs Predicted")
plt.plot([0,48],[0,48],'r')
plt.show()