
행렬 정의
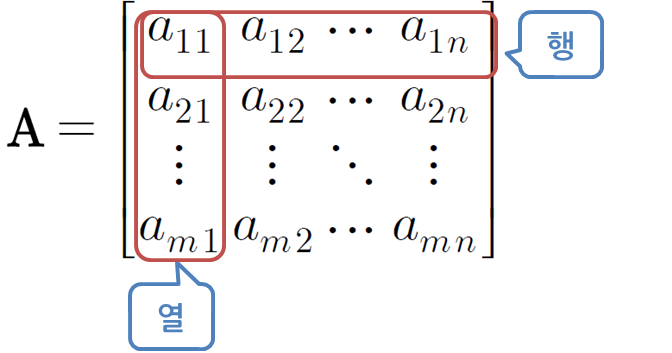
m개의 행(row)과 n개의 열(column)으로 이루어진 행렬을 m by n matrix라 읽는다.
항등행렬이란?
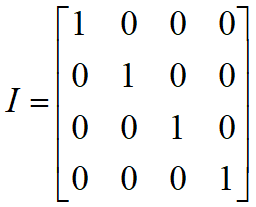
대각선 성분만 1이고 나머지는 0인 행렬을 말한다.
전치행렬이란?
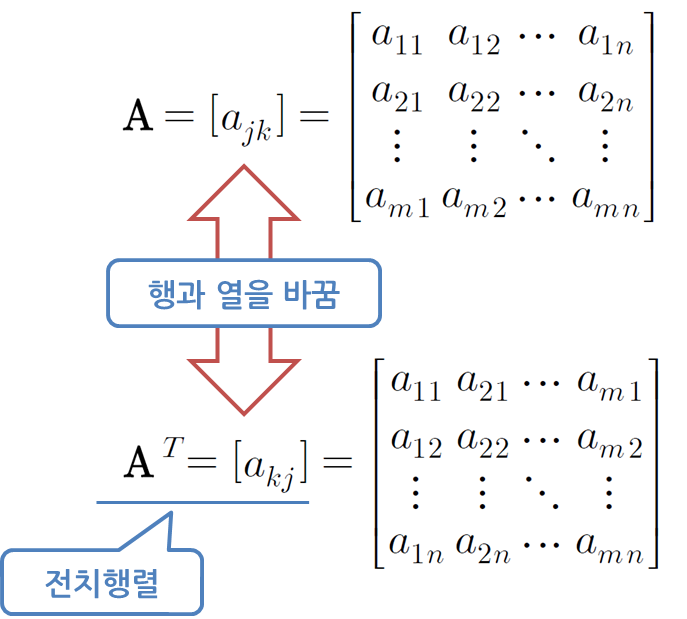
행렬의 전치 : 임의 행렬의 열과 행을 바꿔 새로운 행렬을 구성한다는 의미
j행 k열의 원소 -> k행 j열의 원소
행렬 연산
-
행렬 간의 합과 차는 행렬의 크기가 같을 때만 계산 가능하다.
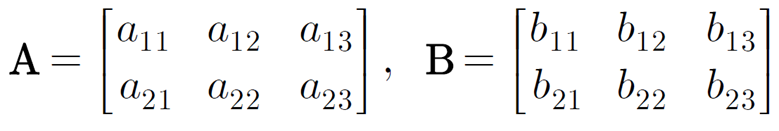
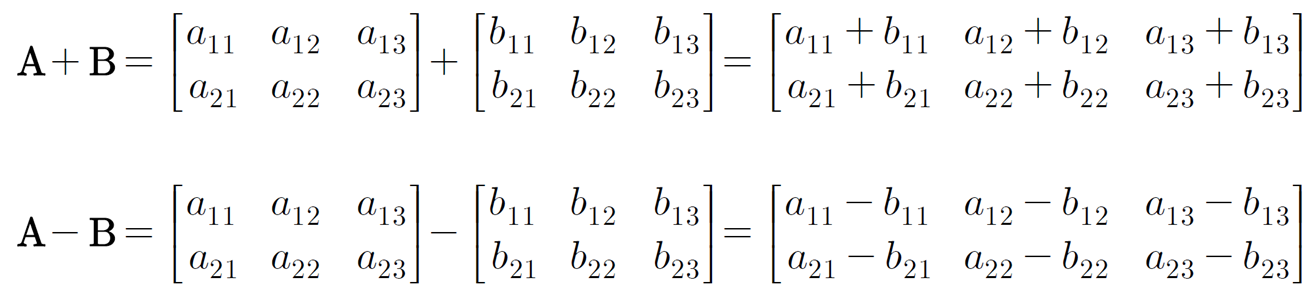
-
행렬과 스칼라의 곱
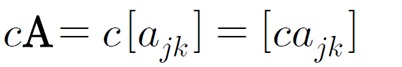
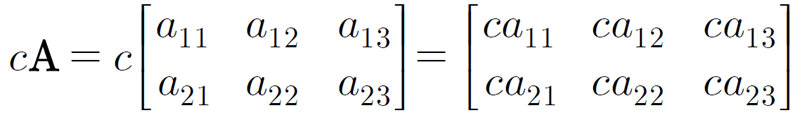
각 원소에 스칼라 값을 곱해준다.
- 행렬 곱인 두 행렬 A와 B의 곱 𝐶 = 𝐴×𝐵가 가능하려면, 첫 번째 행렬 𝐴의 열(column) 개수와 두 번째 행렬 𝐵의 행(row) 개수가 같아야 한다.
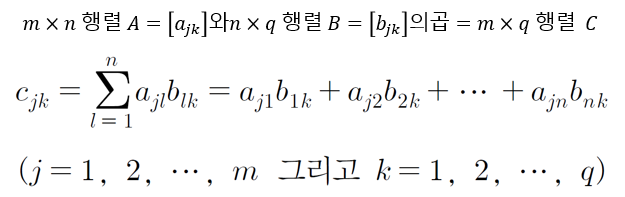
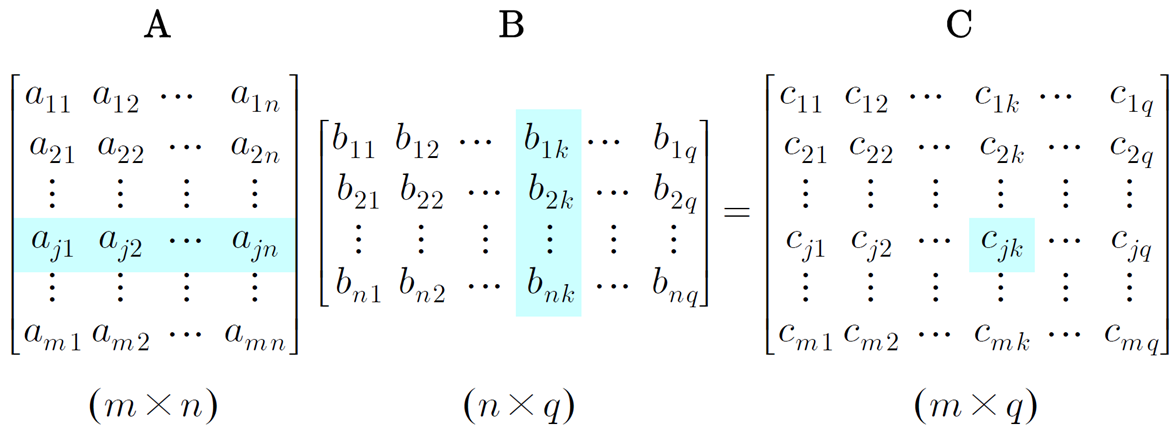
위와 같이 m by q 행렬을 구할 수 있다.
- 벡터의 내적
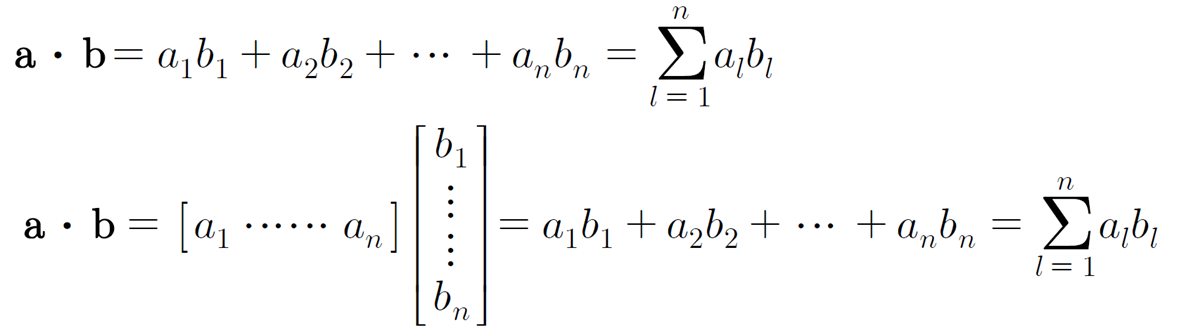
행렬의 곱셈은 벡터내적을 모아 놓은 것이다
행렬의 성질
결합법칙, 분배법칙은 가능하나 교환법칙은 불가능!
* 행렬의 곱셈을 해보기만 해도 알 수 있음 특히 Transform을 하는 과정에서 이 중요성이 두드러지는데
애들하고 얘기했던 과정... 이제 이걸 정리해보자면
Transform은 Scale Rotation Translation 행렬의 순서로 이루어진다.
이 순서를 반드시 지켜줘야하는데, 이는 x,y축을 기저벡터로 이용하기 때문이다.
1) srt 순서대로 행렬곱을 했을 때
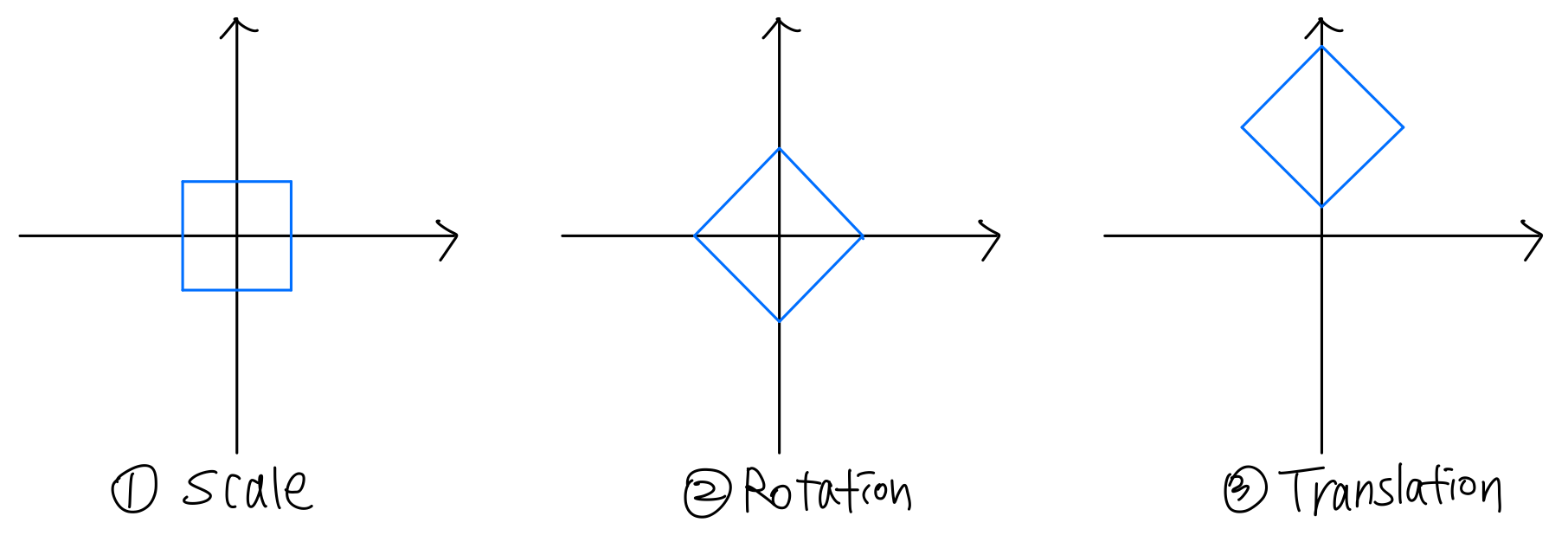
2) 임의로 str 순서를 바꾸어줬을 때
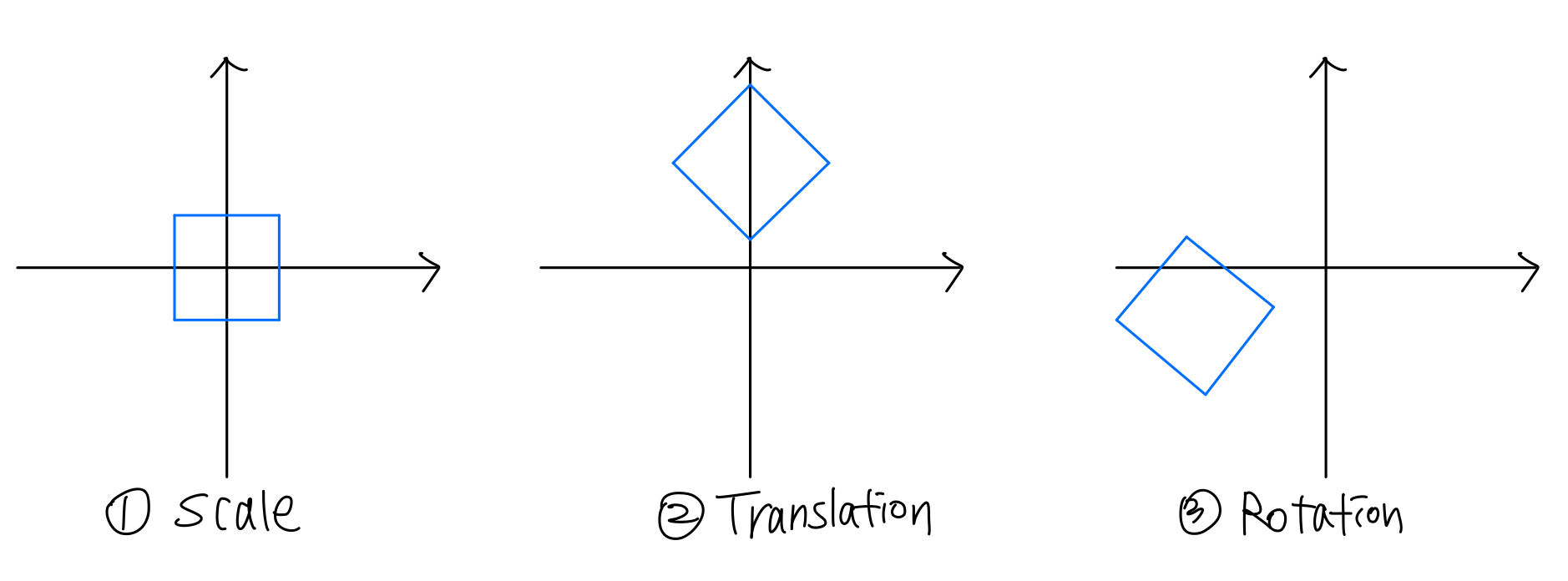
아마도 우리가 원하는 좌표이동은 1번과 같은 형태일 것이다.
기저를 중심으로 회전을 해야 우리가 일반적으로 생각하는 변환이 가능해진다.
행렬의 종류
특히 중요한 역행렬
너 누군데
우선 역행렬의 값은 역행렬을 구하고자하는 행렬과 그 역행렬의 곱이 단위행렬가 되는 행렬을 말한다.

이 그림을 가지고 역행렬과 카메라 좌표계의 관계를 이해해보자.
카메라가 오른쪽으로 움직인다고 가정할 때, 오브젝트는 왼쪽으로 움직이는 것처럼 보일 것이다.
이는 카메라 좌표를 기준으로 오브젝트의 x좌표가 계속 -가 되어가고 있다는 것이다.
그렇기 때문에 위처럼 역행렬을 곱해도 되고,
카메라 좌표의 x,y 축에 -를 곱한 값이 플레이어의 좌표라고 생각해도 된다!
