벡터 정의
- 벡터(vector) : 크기와 방향에 의해 결정되는 양 (크기 + 방향)
- 스칼라(scalar) : 크기에 의해서만 결정되는 양 (크기)
scalar는 scale(크기, 축적)에서 온 것으로 1을 기준으로 몇배인가라는 의미
10g은 1g의 10배. 0.1g은 1g의 1/10배라는 뜻이다.
- 시점(P) : 벡터가 시작되는 화살표의 꼬리
- 종점(Q) : 벡터의 마지막 부분인 화살표의 머리
- 크기(a) : 방향과 상관없는 화살표의 길이
3차원에서의 벡터의 크기는 피타고라스 정리에 의해
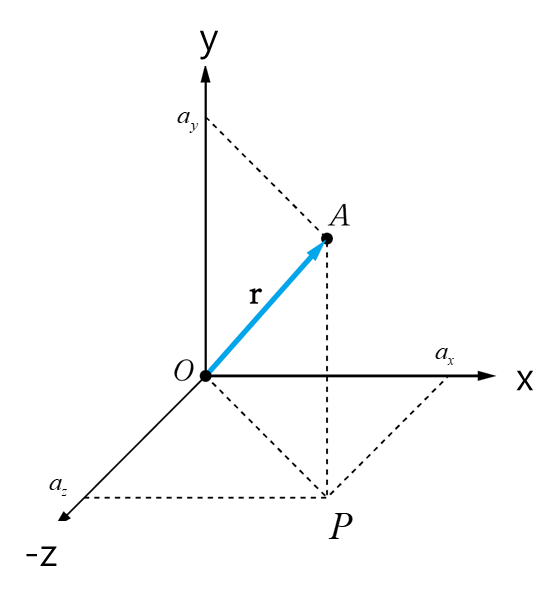
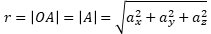
로 정의 될 수 있다.
(2차원은 아래와 같다.)
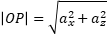
벡터 종류
- 단위 벡터
- 벡터의 크기가 1인 벡터를 단위벡터(unit vector)라 한다.
- 벡터의 크기를 1로 만드는 행위를 정규화(normalize)라고 한다.
- 𝑉=(𝑣𝑥, 𝑣𝑦, 𝑣𝑧) 라 할 때, 단위벡터 𝑈𝑣는
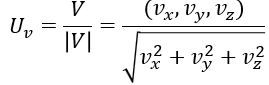로 정의한다.
음, 쉽게 생각해서 벡터와 벡텅 크기의 역수를 곱한다고 생각하면 된다.
벡터 크기(|𝑉|에 1을 대입하면 원래 벡터가 나옴 ㅇㅇ)
벡터 연산
-
덧셈
-
스칼라곱
-
뺄셈
-
내적
※ scalar product : 벡터의 방향성이 사라지고 크기값만 남음
𝐴=(𝑎𝑥, 𝑎𝑦, 𝑎𝑧) 𝐵=(𝑏𝑥, 𝑏𝑦, 𝑏𝑧)
=> 𝐴•𝐵=𝑎𝑥𝑏𝑥 + 𝑎𝑦𝑏𝑦 + 𝑎𝑧𝑏𝑧 = |𝐴||𝐵|cos𝜃
여기서 A,B가 단위벡터라면 |𝐴| = |𝐵| = 1 이므로
=> 𝐴•𝐵=𝑎𝑥𝑏𝑥 + 𝑎𝑦𝑏𝑦 + 𝑎𝑧𝑏𝑧 = cos𝜃-> 증명
증명 들어가기 전, 코사인 제 2법칙이 무엇인지를 알아보자면
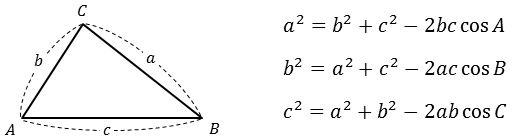
이고, 이를 통해
내적 값을 증명할 수 있게 되었습니다.
+ 내적의 유용성이라고 하면
1.내적은 곱셈 세번, 덧셈 두번으로 연산비용이 저렴하다.
2. 이 저렴한 연산으로 cos()값을 얻기 때문이 매우 유용하다
이해가 잘 안돼서 책직핃티에게 물어보니
~cos 그래프 참고~
위 그래프를 참고해서 사잇각을 알아낼 수 있는데
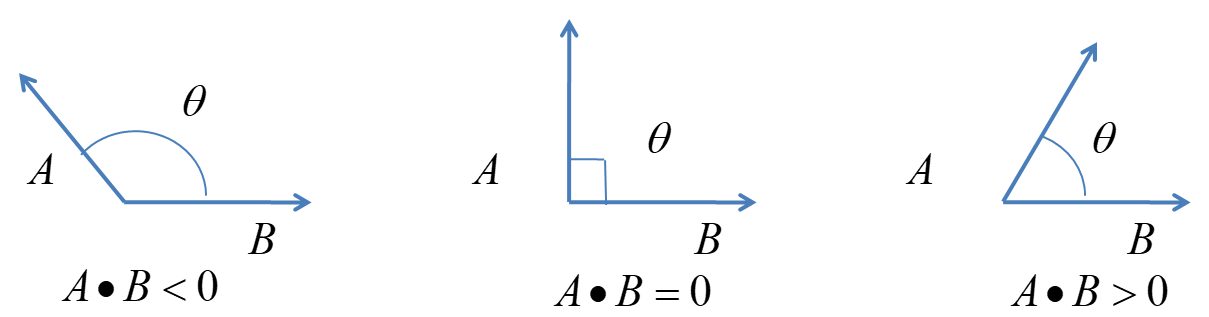
-> 용도
1. 확산광 계산
2. 가시성 판단
3. 방향 계산
4. 투영
- 외적
-> 증명
-> 용도
- 면의 법선벡터
- 평행사변형 면적
