스택(stack)

• 자료(data element)를 보관할 수 있는 (선형)구조

• 단, 넣을 때에는 한 쪽 끝에서 밀어 넣는다

  → 푸시(Push)연산

• 꺼낼 때에는 같은 쪽에서 뽑아 꺼내야 한다

  → 팝(Pop)연산

• 후입선출(LIFO, Last-In First-Out) 특징을 가지는 선형 자료구조
  

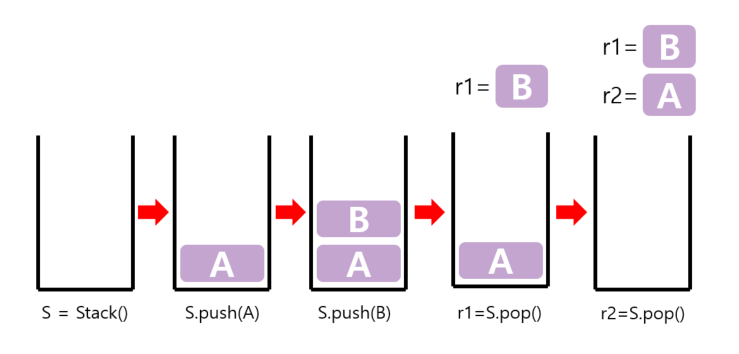
• 초기 상태 : 비어 있는 스택(empy stack)

  • S = Stack()

• 데이터 원소 A를 스택에 추가

  • S.push(A)
  • S.push(B)

• 데이터 원소 꺼내기

  • r1 = S.pop()
  • r2 = S.pop()

스택에서 발생하는 오류

• 비어 있는 스택에서 데이터 원소를 꺼내려 할 때

  • r3 = S.pop()

    → 스택 언더플로우(stack underflow)

• 꽉 찬 스택에 데이터 원소를 넣으려 할 때

  → 스택 오버플로우(stack overflow)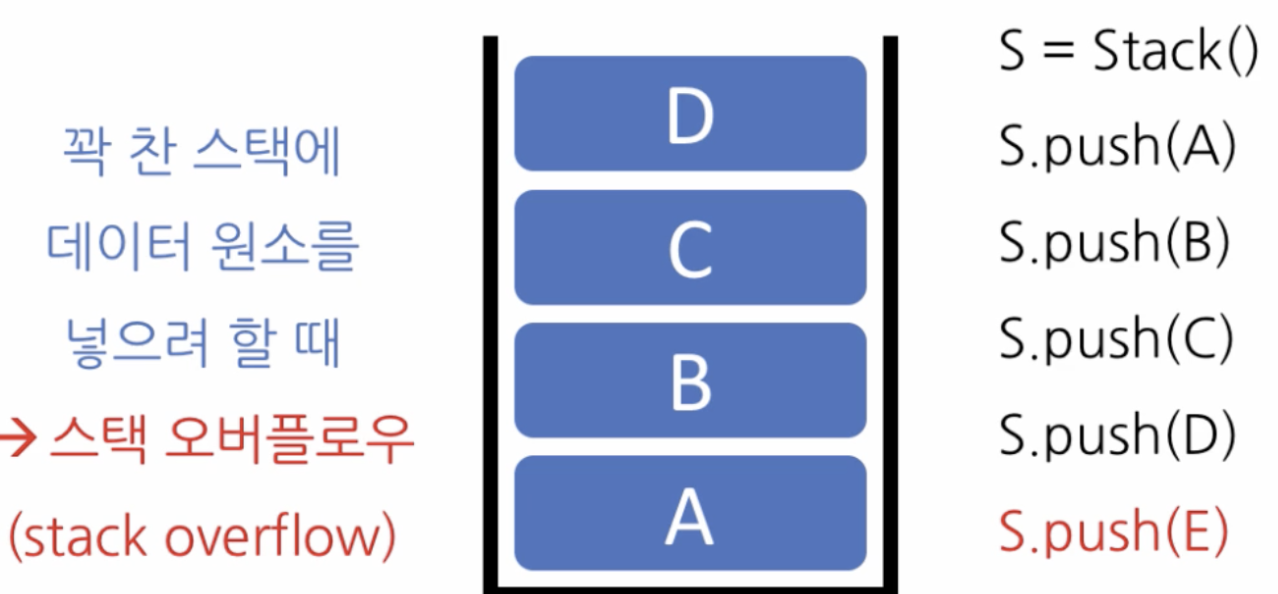

  

스택의 추상적 자료구조 구현

1. 배열(array)를 이용하여 구현

• python 리스트와 메서드를 이용하여 구현

2. 연결 리스트(Linked list)를 이용하여 구현

• 양방향 연결 리스트를 이용

연산의 정의

• size(): 현재 스택에 들어 있는 데이터 원소의 수를 구함
• isEmpty(): 현재 스택이 비어 있는지를 판단 (size() == 0?)
• push(x): 데이터 원소 x 를 스택에 추가
• pop(): 스택에 가장 나중에 저장된 데이터 원소를 제거 (또한, 반환)
• peek(): 스택에 가장 나중에 저장된 데이터 원소를 참조 (반환), 그러나 제거하지는 않음

배열로 구현한 스택

class ArrayStack:

	def size(self): # 스택의 크기를 리턴
		return len(self.data)

	def isEmpty(self): # 스택이 비어 있는지 판단
		return self.size() == 0

	def push(self, item): # 데이터 원소를 추가
		self.data.append(item)

	def pop(self): # 데이터 원소를 삭제(리턴)
		return self.data.pop()

	def peek(self): # 스택의 꼭대기 원소 반환
		return self.data[-1]

양방향 연결 리스트를 이용하여 구현한 스택

from doubly_linked_list import Node
from doubly_linked_list import DoublyLinkedList # 양방향 연결 리스트를 불러옴

class LinkedListStack:

	def __init__(self):
		self.data = DoublyLinkedList()

	def size(self): # 스택의 크기를 리턴
		return self.data.getLength()

	def isEmpty(self): # 스택이 비어 있는지 판단
		return self.size() == 0

	def push(self, item): # 데이터 원소를 추가
		node = Node(item)
		self.data.insertAt(self.size() + 1, node)

	def pop(self): # 데이터 원소를 삭제(리턴)
		return self.data.popAt(self.size())

	def peek(self): # 스택의 꼭대기 원소 반환
		return self.data.getAt(self.size()).data

수식의 괄요 유효성 검사

올바른 수식

• (A + B)
• {(A + B) * C}
• [(A + B) * (C + D)]

올바르지 않은 수식

• (A + B
• A + B)
• {A * (B + C}(
• [(A + B) * (C + D)}

알고리즘 설계

• 수식을 왼쪽부터 한 글자씩 읽음
• 여는 괄호 - ( 또는 { 또는 [ 를 만나면 스택에 푸시
• 닫는 괄호 - ) 또는 } 또는 ] 를 만나면
  • 스택이 비어 있으면 올바르지 않은 수식
  • 스택에서 pop, 쌍을 이루는 여는 괄호 인지 검사
    • 맞니 안ㄹ으면 올바르지 않은 수식
• 끝까지 검사한 후, 스택이 비어 있어야 올바른 수식

[실습] 수식의 괄호 검사(스택)

참고

수식의 괄요 유효성 검사

올바른 수식

• (A + B)
• {(A + B) * C}
• [(A + B) * (C + D)]

올바르지 않은 수식

• (A + B
• A + B)
• {A * (B + C}(
• [(A + B) * (C + D)}

알고리즘 설계

• 수식을 왼쪽부터 한 글자씩 읽음
• 여는 괄호 - ( 또는 { 또는 [ 를 만나면 스택에 푸시
• 닫는 괄호 - ) 또는 } 또는 ] 를 만나면
  • 스택이 비어 있으면 올바르지 않은 수식
  • 스택에서 pop, 쌍을 이루는 여는 괄호 인지 검사
    • 맞니 안ㄹ으면 올바르지 않은 수식
• 끝까지 검사한 후, 스택이 비어 있어야 올바른 수식

---

문제

어서와! 자료구조와 알고리즘은 처음이지? 11강 실습:수식의 괄호 검사 (스택)

문제 설명

소괄호: ( )중괄호: { }대괄호: 를 포함할 수 있는 수식을 표현한 문자열 expr 이 인자로 주어질 때, 이 수식의 괄호가 올바르게 여닫혀 있는지를 판단하는 함수 solution() 을 완성하세요. 이 함수는 수식의 괄호가 유효하면 True 를, 그렇지 않으면 False 를 리턴합니다.

스택을 활용하여 수식 내의 괄호 여닫음의 유효성을 검사하는 알고리즘에 대해서는 동영상 강의 내용을 참고하세요.

---

나의 풀이

solution.py

class ArrayStack:

    def __init__(self):
        self.data = []

    def size(self):
        return len(self.data)

    def isEmpty(self):
        return self.size() == 0

    def push(self, item):
        self.data.append(item)

    def pop(self):
        return self.data.pop()

    def peek(self):
        return self.data[-1]

def solution(expr):
    
    match = {
        ')' : '(',
        '}' : '{',
        ']' : '['
    }
    
    S = ArrayStack()

    for c in expr:
        if c in '({[' :
            S.push(c)
        elif c in match:
            if S.isEmpty():
                return False
            else:
                t = S.pop()
                if t != match[c]:
                    return False
    return S.isEmpty()

실행 결과

정확성  테스트
테스트 1 〉	통과 (0.04ms, 10.9MB)
테스트 2 〉	통과 (0.04ms, 10.9MB)
테스트 3 〉	통과 (0.04ms, 10.8MB)
테스트 4 〉	통과 (0.04ms, 10.8MB)
테스트 5 〉	통과 (0.06ms, 10.7MB)
테스트 6 〉	통과 (0.04ms, 10.7MB)
채점 결과
정확성: 100.0
합계: 100.0 / 100.0