중위 표기법(Infix Notation)

• 연산자가 피연산자들의 사이에 위치
• (A + B) * (C + D)

후위 표기법(Postfix Notation)

• 연산자가 피연산자들의 뒤에 위치
• AB + CD + *

---

중위 표현식 → 후위 표현식

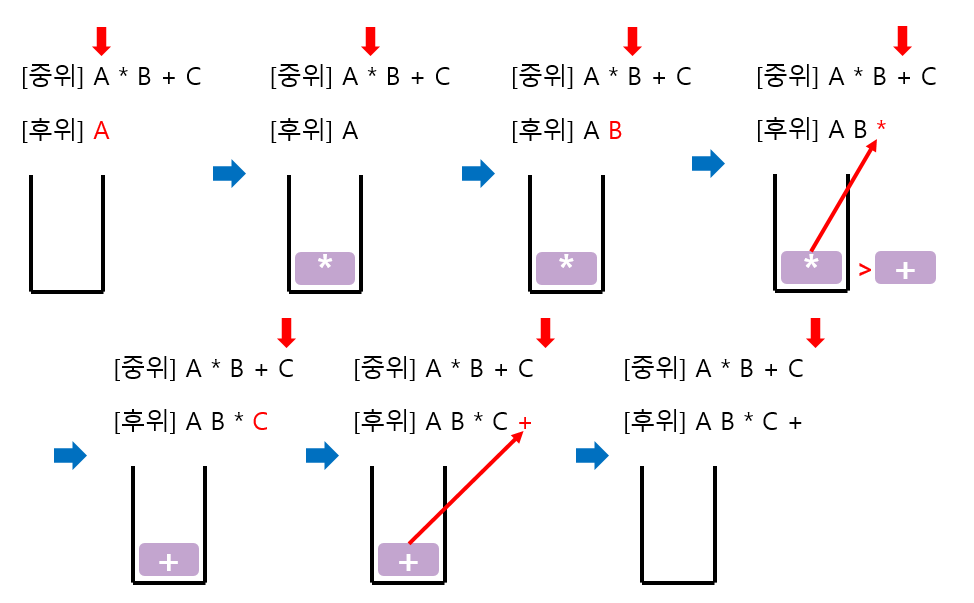
1. 예시 A * B + C

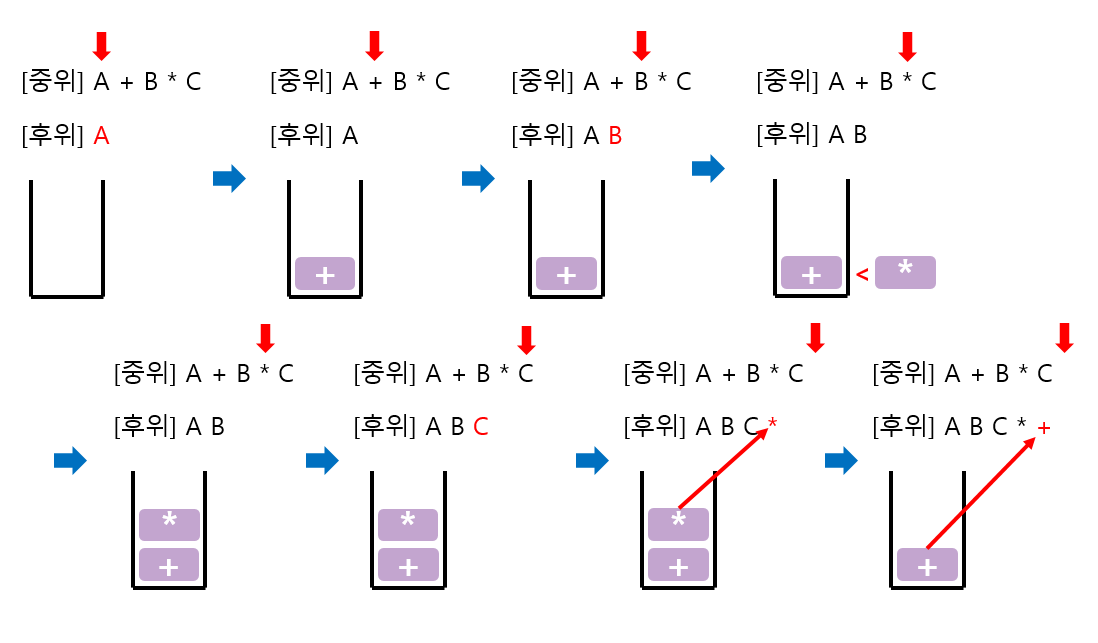
2. 예시 A + B * C

괄호의 처리

[중위] (A + B) * C

[후위] A B + C *

• 여는 괄호는 스택에 push
• 닫는 괄호를 만나면 여는 괄호가 나올 때까지 pop

→ 괄호안에 있는 내용들 먼저 pop

[중위] A * (B + C)

[후위] A B C + *

• 연산자를 만났을 때, 여는 괄호 너머까지 pop 하지 않도록
• 여는 괄호 우선순위는 가장 낮게 설정

알고리즘의 설계

• 연산자의 우선순위 설정

prec = {
	'*' : 3,
	'/' : 3,
	'+' : 2,
	'-' : 2,
	'(' : 1
}

• 중위 표현식을 왼쪽부터 한 글자씩 읽어서
  • 피연산지연 그냥 출력
    • (이면 스택에 push
    • ) 이면 ) 이 나올 때까지 스택에서 pop 그리고 출력
  • 연산자이면 스택에서 이보다 높(거나 같)은 우선순위 것들을 pop 그리고 출력
    • 그리고 이 연산자는 스택에 push
• 스택에 남아 있는 연산자는 모두 pop 그리고 출력

[실습] 중위표현 수식 → 후위표현 수식

참고

• 스택의 맨 위에 있는 연산자와의 우선순위 비교

  → 스택의 peek() 연산 이용

• 스택에 남아 있는 연산자 모두 pop() 하는 순환문

  → while not opStack.isEmpty()

문제

어서와! 자료구조와 알고리즘은 처음이지? 12강 실습:중위표현 수식 --> 후위표현 수식

문제 설명

중위 표기법을 따르는 수식 S 가 인자로 주어질 때, 이 수식을 후위 표기법을 따르는 수식으로 변환하여 반환하는 함수 solution() 을 완성하세요.

인자로 주어지는 수식 문자열 S 는 영문 대문자 알파벳 한 글자로 이루어지는 변수 A - Z 까지와 4칙연산을 나타내는 연산자 기호 +, -, *, /, 그리고 여는 괄호와 닫는 괄호 (, ) 로 이루어져 있으며 공백 문자는 포함하지 않는 것으로 가정합니다. 또한, 올바르게 구성되지 않은 수식은 인자로 주어지지 않는다고 가정합니다. (수식의 유효성은 검증할 필요가 없습니다.)

문제에서 미리 주어진, 연산자의 우선순위를 표현한 python dict 인 prec 을 활용할 수 있습니다.

또한, 스택의 기초 강의에서 이미 구현한, 배열을 이용한 스택의 추상적 자료 구조 코드가 이미 포함되어 있으므로 그대로 이용할 수 있습니다.

• (참고) 테스트 케이스를 보완하여 문제가 2019년 9월 24일에 수정되었습니다.

---

나의 풀이

• 피연산자이면 그대로 출력
  • ( 이면 스택에 push
  • ) 이면 ( 나올때 까지 스택에서 pop 그리고 출력
• 연산자이면 스택에서 이보다 높거나 같은 우선순위 들을 pop
  그리고 이 연산자는 스택에 push
• 스택에 남아 있는 연잔자는 모두 pop 그리고 출력

solution.py

class ArrayStack:

    def __init__(self):
        self.data = []

    def size(self):
        return len(self.data)

    def isEmpty(self):
        return self.size() == 0

    def push(self, item):
        self.data.append(item)

    def pop(self):
        return self.data.pop()

    def peek(self):
        return self.data[-1]

prec = {
    '*': 3, '/': 3,
    '+': 2, '-': 2,
    '(': 1
}

def solution(S):
    stack = []
    answer = ''
    for c in S:
        if c not in '()+-*/':
            answer += c
        elif  c == '(':
            stack.append(c)
        elif c == ')':
            while stack[-1] != '(':
                answer += stack.pop()
            stack.pop()
        elif stack and prec[c] <= prec[stack[-1]]:
            answer += stack.pop()
            stack.append(c)
        else:
            stack.append(c)
            
    while stack:
        answer += stack.pop()
                
    return answer

실행결과

정확성  테스트
테스트 1 〉	통과 (0.05ms, 10.7MB)
테스트 2 〉	통과 (0.04ms, 10.9MB)
테스트 3 〉	통과 (0.04ms, 10.7MB)
테스트 4 〉	통과 (0.05ms, 10.7MB)
테스트 5 〉	통과 (0.04ms, 10.9MB)
테스트 6 〉	통과 (0.04ms, 10.8MB)
테스트 7 〉	실패 (0.24ms, 10.7MB)
테스트 8 〉	실패 (0.27ms, 10.7MB)
채점 결과
정확성: 75.0
합계: 75.0 / 100.0

• 입력되는 값이 공백이 있을 경우를 생각해야함
• 피연산자가 숫자인 경우도 생각해서 제거해야함

나의 풀이_2

• 들어오는 값이 공백 또는 숫자인 경우를 생각해서 split(공백제거)하는 메소드
  그리고 후위표현 수식으로 변경하는 메소드로 나눠서 구현

solution_2.py

class ArrayStack:

    def __init__(self):
        self.data = []

    def size(self):
        return len(self.data)

    def isEmpty(self):
        return self.size() == 0

    def push(self, item):
        self.data.append(item)

    def pop(self):
        return self.data.pop()

    def peek(self):
        return self.data[-1]

prec = {
    '*': 3, '/': 3,
    '+': 2, '-': 2,
    '(': 1
}

# 수식이 문자열로 주어져 있을 때 (몇자리수인지 모르는 상태)
# 각각을 피연산자인 수와 연산자인 기호로 분리해서 리스트로 만드는 작업
# exprStr -> 중위표현 수식
def splitTokens(expStr):
    tokens = []
    val = 0 # 각 자리 숫자를 담은 변수
    valProcessing = False # 변수프로세스 false로 초기화
    for c in expStr:
        if c == ' ': # 빈칸이 들어 있으면 패스
            continue
        if c in '0123456789': # 숫자를 10진수로 변환하는 과정
            val = val * 10 + int(c)
            valProcessing = True # 숫자를 만났음으로 True로 변환
        else:
            if valProcessing:
                tokens.append(val)
                val = 0 
            valProcessing = False # 10진수가 아님으로 False로 다시 변환
            tokens.append(c)
    if valProcessing: # 변수프로세스 확인 후 변수처리
        tokens.append(val)
    return tokens

def infixToPostfix(s): # 중위표현 수식 -> 후위표현 수식 변경 작업
    re = ''
    stack = []
    for c in s: 
        if type(c) is int: # 수식이 숫자이면 바로 re에 담음
            re += str(c)
        elif c not in '()+-*/': # 수식이 연산자가 아니면 re에 담음
            re += c
        elif c == "(": # 수식이 '('이면 stack에 넣음
            stack.append(c)
        elif stack and c == ")": # stack이 있고, ')'라면, stack 마지막이 '('아닐때까지 stack에서 꺼내서 re에 담음
            while stack[-1] != "(":
                re += stack.pop()
            stack.pop()
        elif stack and prec.get(c) <= prec.get(stack[-1]): # stack에 값이 있고, prec에 수식이 stack마지막 값보다 같거나 작다면
            re += stack.pop() # stack에서 꺼내서 re에 담은
            stack.append(c) # stack에 수식을 넣음
            if len(stack) == 2: # stack의 길이가 2라면, stack의 첫번째 값을 re에 담음
                re += stack.pop(0)
        else:
            stack.append(c) # 위에 해당하지 않은 수식은 stack에 담음
            
    while stack: # stack에 남아있는 수식을 re에 담음
        re += stack.pop()
                
    return re

    
def solution(expr):
    tokens = splitTokens(expr)
    postfix = infixToPostfix(tokens)
    
    return postfix