[알고리즘] BOJ 3687 성냥개비

[BOJ] 3687 성냥개비 바로가기

📍 문제

성냥개비는 숫자를 나타내기에 아주 이상적인 도구이다. 보통 십진수를 성냥개비로 표현하는 방법은 다음과 같다.

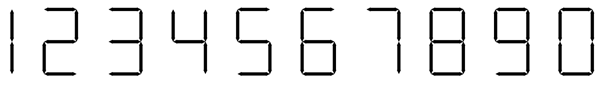
성냥개비의 개수가 주어졌을 때, 성냥개비를 모두 사용해서 만들 수 있는 가장 작은 수와 큰 수를 찾는 프로그램을 작성하시오.

---

📍 입력

첫째 줄에 테스트 케이스의 개수가 주어진다. 테스트 케이스는 최대 100개 이다. 각 테스트 케이스는 한 줄로 이루어져 있고, 성냥개비의 개수 n이 주어진다. (2 ≤ n ≤ 100)

---

📍 출력

각 테스트 케이스에 대해서 입력으로 주어진 성냥개비를 모두 사용해서 만들 수 있는 가장 작은 수와 가장 큰 수를 출력한다. 두 숫자는 모두 양수이어야 하고, 숫자는 0으로 시작할 수 없다.

---

📍 풀이

✍ 적용 알고리즘

• 동적 프로그래밍(Dynamic Programming) 알고리즘을 적용하여 문제를 해결하였다.

✍ 문제 풀이

📌 현재 성냥개비 수(n)로 만들 수 있는 가장 큰 수를 만드는 법

• 현재 성냥개비 수(n)가 짝수인 경우는 숫자의 자리수를 최대로 만들기 위해서 가장 적은 성냥개비 수 2개를 소모하는 숫자 1 을 사용하여 숫자를 생성한다.
• Ex) 현재 성냥개비 수(n)가 8 일 경우 성냥개비를 2 2 2 2로 나눈 후 모두 숫자 1로 바꾸어주면 1111 이라는 가장 큰 수를 얻을 수 있다.
• 현재 성냥개비 수(n)가 홀수인 경우는 숫자의 자리수를 최대로 만들기 위해서 가장 적은 성냥개비를 소모하는 숫자 1 을 최대한으로 사용한 후 숫자 1 다음으로 적은 성냥개비를 소모하는 숫자 7 을 사용하여 숫자를 생성한다.
• Ex) 현재 성냥개비 수(n)가 9 일 경우 성냥개비를 3 2 2 2로 나눈 후 성냥개비 3개는 숫자 7 로 성냥개비 2개는 숫자 1로 바꾸어주면 7111 이라는 가장 큰 수를 얻을 수 있다.

📌 현재 성냥개비 수(n)로 만들 수 있는 가장 작은 수를 만드는 법

• 2개부터 8개까지 성냥개비로 만들 수 있는 가장 작은 수 리스트(dp)를 생성한다.
• 2개부터 7개까지 성냥개비로 만들 수 있는 가장 작은 수 딕셔너리(D)를 생성한다.
• 9 부터 100 까지의 성냥개비로 만들 수 있는 가장 작은 수를 구하기 위해서 현재 성냥개비 수(n)에서 2 ~ 7(k) 만큼의 성냥개비 수를 뺀 n - k 개의 성냥개비로 만들 수 있는 값 중 가장 작은 값을 dp 리스트에서 추출한 후 그 값에 k 개의 성냥개비로 만들 수 있는 가장 작은 수를 D 딕셔너리에서 추출하여 합친 값 중 가장 작은 값을 dp 리스트에 추가한다.
• Ex) 현재 성냥개비 수(n)가 9 일 경우 아래와 같은 경우가 존재한다.
  • dp[2] + D[7] = 18
  • dp[3] + D[6] = 70
  • dp[4] + D[5] = 42
  • dp[5] + D[4] = 24
  • dp[6] + D[3] = 67
  • dp[7] + D[2] = 81
• 이 값들 중 가장 작은 값인 18 을 dp 리스트에 추가한다.

✍ 코드

from sys import stdin

dp = [0,0,1,7,4,2,6,8,10] # 성냥개비 n개로 만들 수 있는 가장 작은 수의 배열
D = {2: 1, 3: 7, 4: 4, 5: 2, 6: 0, 7: 8} # 성냥개비 2~7개로 만들 수 있는 가장 작은 수
for n in range(9,101):
    # 현재 성냥개비 수로 만들 수 있는 경우의 수 중에서 가장 작은 값을 dp에 추가
    element = min(dp[n-7]*10 + D[7], dp[n-6]*10 + D[6], dp[n-5]*10 + D[5], dp[n-4]*10 + D[4], dp[n-3]*10 + D[3], dp[n-2]*10 + D[2])
    dp.append(element)

T = int(stdin.readline())
for _ in range(T):
    n = int(stdin.readline())
    # 홀수일 경우
    if n%2: MAX = '7' + '1' * ((n - 3) // 2)
    else: MAX = '1' * (n // 2)
    print(dp[n],MAX)