[Programmers] 교점에 별 만들기 바로가기
📍 문제 설명
Ax + By + C = 0 으로 표현할 수 있는 n 개의 직선이 주어질 때, 이 직선의 교점 중 정수 좌표에 별을 그리려 합니다.
예를 들어, 다음과 같은 직선 5개를
2x - y + 4 = 0-2x - y + 4 = 0-y + 1 = 05x - 8y - 12 = 05x + 8y + 12 = 0
좌표 평면 위에 그리면 아래 그림과 같습니다.
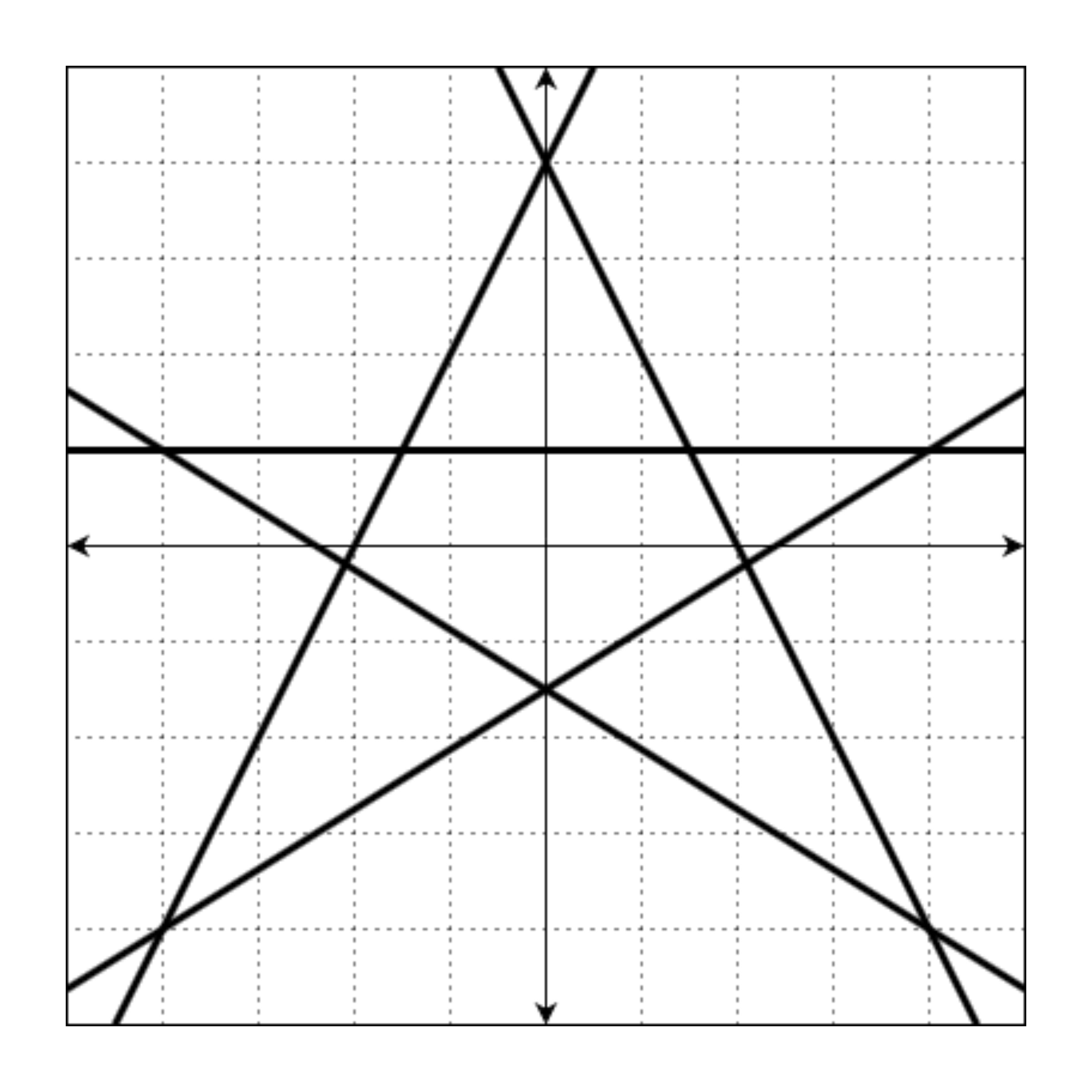
이때, 모든 교점의 좌표는 (4, 1), (4, -4), (-4, -4), (-4, 1), (0, 4), (1.5, 1.0), (2.1, -0.19), (0, -1.5), (-2.1, -0.19), (-1.5, 1.0)입니다. 이 중 정수로만 표현되는 좌표는 (4, 1), (4, -4), (-4, -4), (-4, 1), (0, 4)입니다.
만약 정수로 표현되는 교점에 별을 그리면 다음과 같습니다.
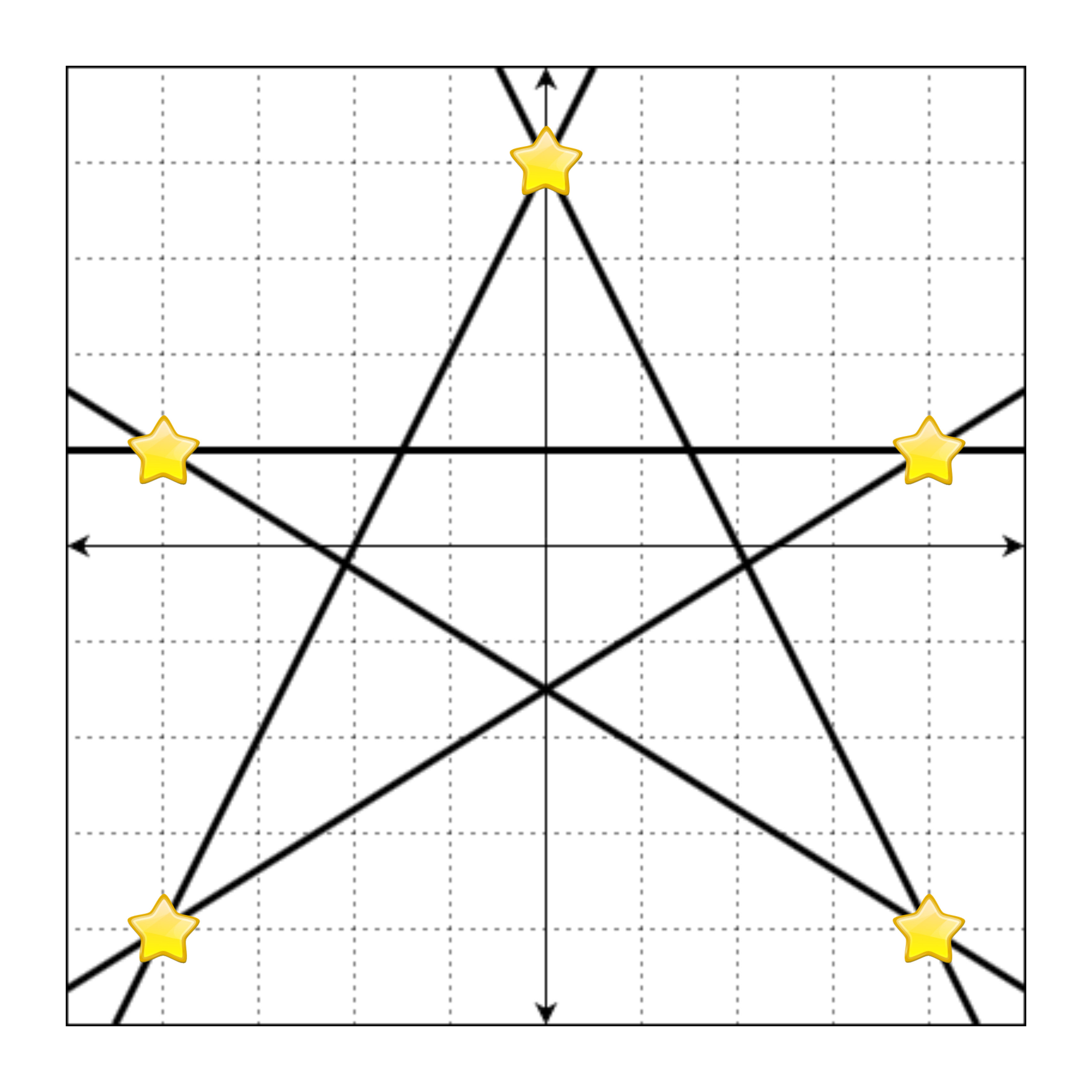
위의 그림을 문자열로 나타낼 때, 별이 그려진 부분은 *, 빈 공간(격자선이 교차하는 지점)은 .으로 표현하면 다음과 같습니다.
"..........."
".....*....."
"..........."
"..........."
".*.......*."
"..........."
"..........."
"..........."
"..........."
".*.......*."
"..........." 이때 격자판은 무한히 넓으니 모든 별을 포함하는 최소한의 크기만 나타내면 됩니다.
따라서 정답은
"....*...."
"........."
"........."
"*.......*"
"........."
"........."
"........."
"........."
"*.......*" 입니다.
직선 A, B, C 에 대한 정보가 담긴 배열 line 이 매개변수로 주어집니다. 이때 모든 별을 포함하는 최소 사각형을 return 하도록 solution 함수를 완성해주세요.
📍 제한 사항
- line의 세로(행) 길이는 2 이상 1,000 이하인 자연수입니다.
- line의 가로(열) 길이는 3입니다.
- line의 각 원소는 [A, B, C] 형태입니다.
- A, B, C는 -100,000 이상 100,000 이하인 정수입니다.
- 무수히 많은 교점이 생기는 직선 쌍은 주어지지 않습니다.
- A = 0이면서 B = 0인 경우는 주어지지 않습니다.
- 정답은 1,000 * 1,000 크기 이내에서 표현됩니다.
- 별이 한 개 이상 그려지는 입력만 주어집니다.
📍 입출력 예
| line | result |
|---|---|
| [[2, -1, 4], [-2, -1, 4], [0, -1, 1], [5, -8, -12], [5, 8, 12]] | ["........", ".........", ".........", ".......", ".........", ".........", ".........", ".........", ".......*"] |
| [[0, 1, -1], [1, 0, -1], [1, 0, 1]] | ["."] |
| [[1, -1, 0], [2, -1, 0]] | ["*"] |
| [[1, -1, 0], [2, -1, 0], [4, -1, 0]] | ["*"] |
📍 입출력 예 설명
입출력 예 #1
문제의 예시와 같습니다.
입출력 예 #2
직선 y = 1, x = 1, x = -1 는 다음과 같습니다.
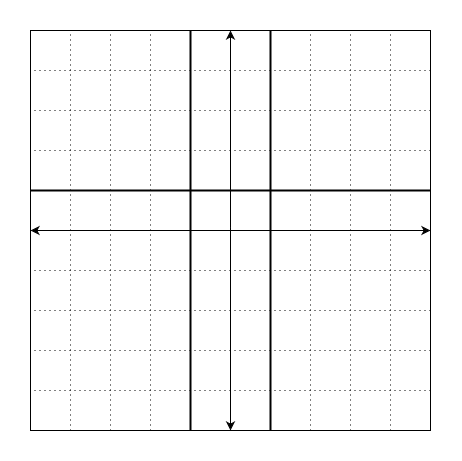
(-1, 1), (1, 1) 에서 교점이 발생합니다.
따라서 정답은
"*.*" 입니다.
입출력 예 #3
직선 y = x, y = 2x 는 다음과 같습니다.
(0, 0) 에서 교점이 발생합니다.
따라서 정답은
"*" 입니다.
입출력 예 #4
직선 y = x, y = 2x, y = 4x 는 다음과 같습니다.
(0, 0) 에서 교점이 발생합니다.
따라서 정답은
"*"입니다.
📍 참고 사항
Ax + By + E = 0
Cx + Dy + F = 0
두 직선의 교점이 유일하게 존재할 경우, 그 교점은 다음과 같습니다.
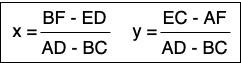
또, AD - BC = 0인 경우 두 직선은 평행 또는 일치합니다.
📍 문제 풀이
📌 풀이 과정
📍 참고사항에서 주어진 정보는 2개이다.- 두 직선
Ax + By + E = 0,Cx + Dy + F = 0에서AD - BC = 0이면 두 직선은 평행 또는 일치한다.- 위 정보의 의미는 두 직선의 기울기가 같기 때문에 교점이 없거나 교점이 무한하다는 것을 의미한다.
- 하지만
📍 제한사항에서 무수히 많은 교점이 생기는 직선 쌍 즉, 같은 값을 가지는 직선 쌍은 주어지지 않는다고 했다. - 따라서
AD - BC = 0인 두 직선은 교점이 없는 직선임을 알 수 있다.
- 두 직선
Ax + By + E = 0,Cx + Dy + F = 0의 교점이 존재할 경우 교점을 구하는 방정식은 아래와 같다.x = (B*F-E*D)/(A*D-B*C), y = (E*C-A*F)/(A*D-B*C)
- 두 직선
calculation(eq1,eq2)함수는 두 직선의 교점의 값을 반환해 주는 함수이다.- 만약 두 직선의 기울기가 같다면 함수를 종료한다.
- 만약 교점인
x, y모두가 정수라면 교점값을 반환한다.
combinations()함수를 통해 2개의 직선을 만들 수 있는 모든 조합을 만든 후 2개의 직선을 인자로calculation()함수를 실행한다.calculation()함수의 결과값을points배열에 저장한다.points배열의 x 값 기준 최대값과 최소값, y 값 기준 최대값과 최소값을w1,w2,h1,h2변수에 저장한다.w1,w2,h1,h2를 활용하여 최소크기의 격자판(answer)을 생성한다.- 교점의 시작점(
w1,h1)을 기준으로points배열에 존재하는 교점들을 격자판에 그려준다.
✍ 코드
from itertools import combinations
def calculation(eq1, eq2):
x1, y1, c1 = eq1 # 직선1
x2, y2, c2 = eq2 # 직선2
# 기울기가 깉아 해가 없는 경우
if x1*y2 == y1*x2:
return
# 두 직선의 해
x = (y1*c2-c1*y2)/(x1*y2-y1*x2)
y = (c1*x2-x1*c2)/(x1*y2-y1*x2)
# 두 직선의 해 x, y가 모두 정수라면 반환
if x == int(x) and y == int(y):
return [int(x), int(y)]
def solution(lines):
points = []
# 모든 선들의 교점 확인
for eq1, eq2 in combinations(lines,2):
point = calculation(eq1,eq2)
if point: points.append(point)
# 그림의 시작점과 마지막점 찾기
w1, w2 = min(points, key = lambda x : x[0])[0], max(points, key = lambda x : x[0])[0] + 1
h1, h2 = min(points, key = lambda x : x[1])[1], max(points, key = lambda x : x[1])[1] + 1
# 별을 포함하는 최소한의 크기 배열 생성
answer = [['.'] * (w2 - w1) for _ in range((h2 - h1))]
# 그림의 시작점을 기준으로 교점 위치 "*" 변환
for x, y in points:
answer[y-h1][x-w1] = '*'
answer.reverse()
return [''.join(a) for a in answer]