[Programmers] 디스크 컨트롤러 바로가기
📍 문제 설명
하드디스크는 한 번에 하나의 작업만 수행할 수 있습니다. 디스크 컨트롤러를 구현하는 방법은 여러 가지가 있습니다. 가장 일반적인 방법은 요청이 들어온 순서대로 처리하는 것입니다.
예를들어
- 0ms 시점에 3ms가 소요되는 A작업 요청
- 1ms 시점에 9ms가 소요되는 B작업 요청
- 2ms 시점에 6ms가 소요되는 C작업 요청와 같은 요청이 들어왔습니다. 이를 그림으로 표현하면 아래와 같습니다.
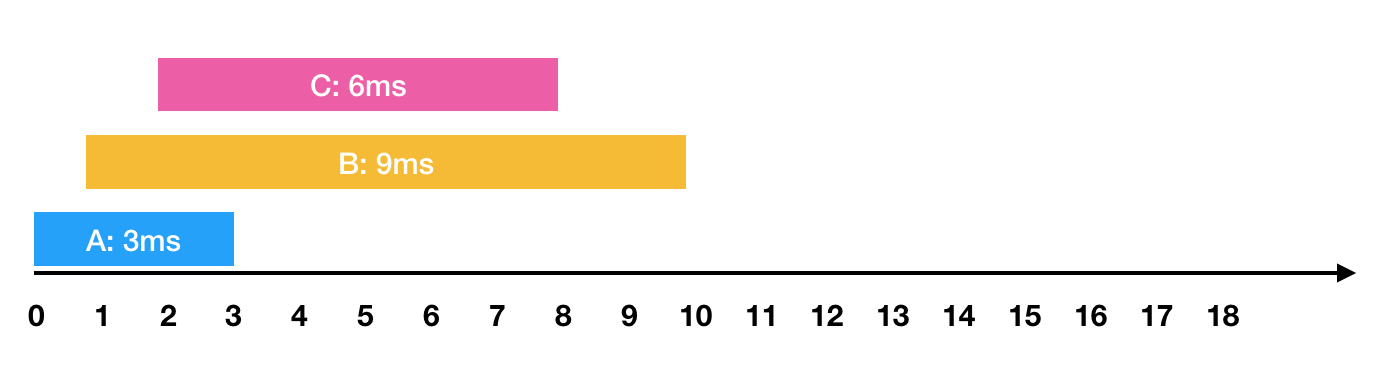
한 번에 하나의 요청만을 수행할 수 있기 때문에 각각의 작업을 요청받은 순서대로 처리하면 다음과 같이 처리 됩니다.
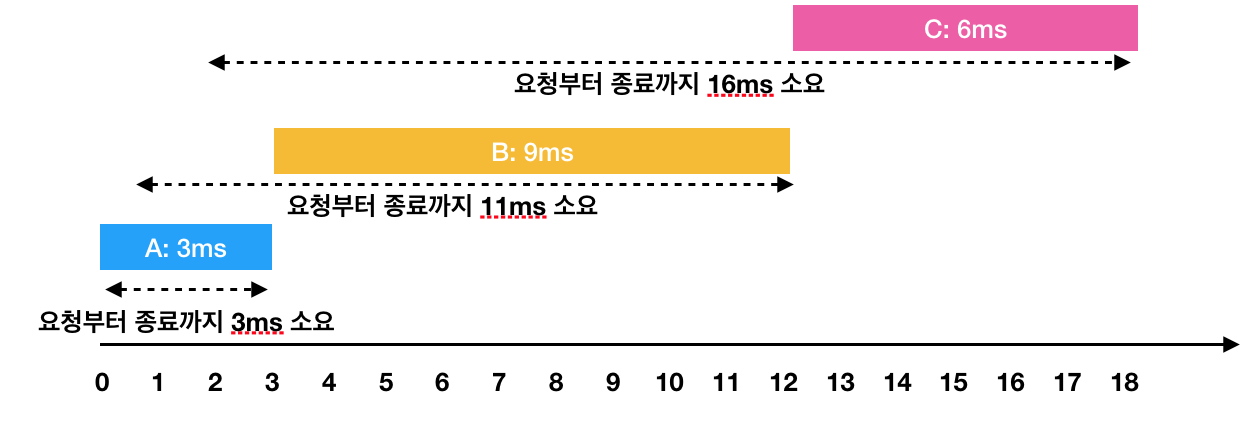
- A: 3ms 시점에 작업 완료 (요청에서 종료까지 : 3ms)
- B: 1ms부터 대기하다가, 3ms 시점에 작업을 시작해서 12ms 시점에 작업 완료(요청에서 종료까지 : 11ms)
- C: 2ms부터 대기하다가, 12ms 시점에 작업을 시작해서 18ms 시점에 작업 완료(요청에서 종료까지 : 16ms)이 때 각 작업의 요청부터 종료까지 걸린 시간의 평균은 10ms(= (3 + 11 + 16) / 3)가 됩니다.
하지만 A → C → B 순서대로 처리하면
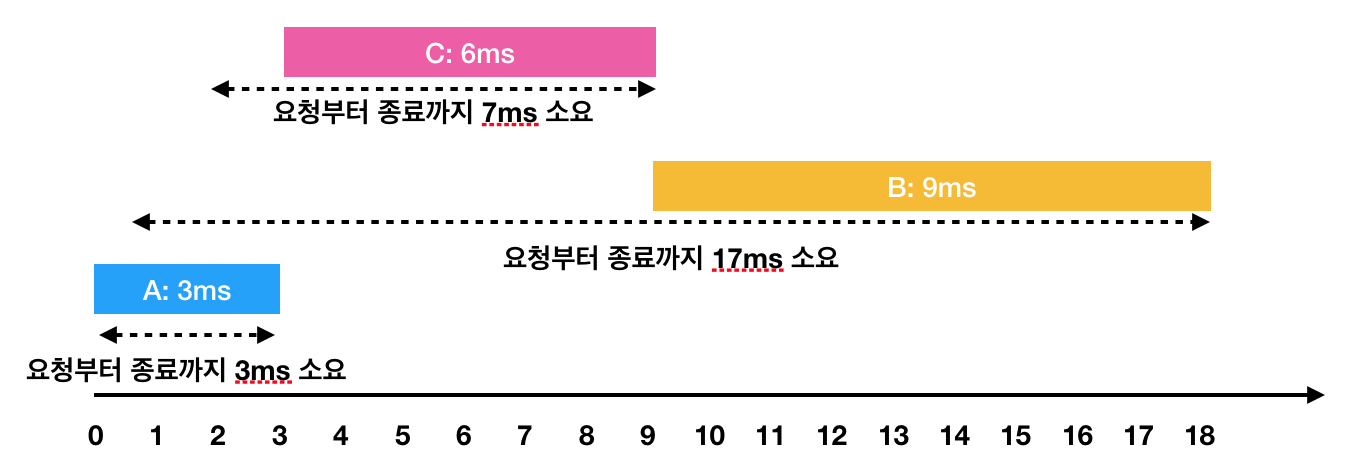
- A: 3ms 시점에 작업 완료(요청에서 종료까지 : 3ms)
- C: 2ms부터 대기하다가, 3ms 시점에 작업을 시작해서 9ms 시점에 작업 완료(요청에서 종료까지 : 7ms)
- B: 1ms부터 대기하다가, 9ms 시점에 작업을 시작해서 18ms 시점에 작업 완료(요청에서 종료까지 : 17ms)이렇게 A → C → B의 순서로 처리하면 각 작업의 요청부터 종료까지 걸린 시간의 평균은 9ms(= (3 + 7 + 17) / 3)가 됩니다.
각 작업에 대해 [작업이 요청되는 시점, 작업의 소요시간]을 담은 2차원 배열 jobs가 매개변수로 주어질 때, 작업의 요청부터 종료까지 걸린 시간의 평균을 가장 줄이는 방법으로 처리하면 평균이 얼마가 되는지 return 하도록 solution 함수를 작성해주세요. (단, 소수점 이하의 수는 버립니다)
📍 제한사항
- jobs의 길이는 1 이상 500 이하입니다.
- jobs의 각 행은 하나의 작업에 대한 [작업이 요청되는 시점, 작업의 소요시간] 입니다.
- 각 작업에 대해 작업이 요청되는 시간은 0 이상 1,000 이하입니다.
- 각 작업에 대해 작업의 소요시간은 1 이상 1,000 이하입니다.
- 하드디스크가 작업을 수행하고 있지 않을 때에는 먼저 요청이 들어온 작업부터 처리합니다.
📍 입출력 예
| jobs | return |
|---|---|
| [[0, 3], [1, 9], [2, 6]] | 9 |
📍 입출력 예 설명
문제에 주어진 예와 같습니다.
- 0ms 시점에 3ms 걸리는 작업 요청이 들어옵니다.
- 1ms 시점에 9ms 걸리는 작업 요청이 들어옵니다.
- 2ms 시점에 6ms 걸리는 작업 요청이 들어옵니다.
📍 풀이
💡 고찰
- 운영체제가 사용하는 스케줄링 기법인 최소 작업 우선 스케줄링(Shortest Job First)을 적용하여 문제를 해결하였다.
- 문제에서 주어진 조건을 제대로 이해하지 못해서 해결하는데 오랜 시간이 걸렸다.
- 작업을 수행할 때 작업 사이에 공백의 시간 없이 주어질 거라고 생각해서 조건 없이 알고리즘을 작성하였더니 정답을 도출할 수 없었다.
- 나중에서야 작업 수행 도중에 공백의 시간이 존재할 수도 있음을 인지하고 코드를 수정하였더니 문제를 해결할 수 있었다.
제한사항에하드디스크가 작업을 수행하고 있지 않을 때에는 먼저 요청이 들어온 작업부터 처리합니다.지문의 의미를 정확하게 이해하지 못한 것이 수 많은 수행착오를 겪게 만든 포인트인 것 같다.- 문제를 내 마음대로 해석하고 이해하려는 자세를 고쳐야 할 것 같다.
📌 문제 풀이
✏️ [1] heap 초기화
requestTime, requireTime = jobs.pop()
heap = [(requireTime, requestTime)]- 작업(
jobs) 중에서 가장 먼저 요청이 들어온 작업을 힙(heap) 자료구조에 추가한다.
✏️ [2] 가장 짧은 시간의 작업 추출
requireTime, requestTime = heappop(heap)- 작업 테이블(
heap)에 존재하는 작업 중 처리시간이 가장 짧은 작업을 추출한다.
✏️ [3] 작업 시간 및 작업 소요시간 갱신
if time < requestTime:
answer += requireTime
time = requestTime + requireTime
else:
answer += (time - requestTime) + requireTime
time += requireTime- 현재 시간(
time) 이후에 요청된 작업의 경우에는 대기 시간 없이 작업이 바로 시작 된다. - 따라서 총 작업 소요시간(
answer)에 처리시간(requireTime)을 누적으로 더한다. - 현재 시간(
time)은 요청 시간(requestTime)에 시작해서 처리시간(requireTime)후에 종료되므로 요청 시간(requestTime)에 + 처리시간(requireTime) 값으로 갱신한다. - 현재 시간 이전에 요청된 작업일 경우에는 작업이 대기한 시간(
time - requestTime)과 처리시간(requireTime)을 누적으로 더한다. - 현재 시간(
time)은 현재 시간에서 처리시간(requireTime)을 더한 값으로 갱신한다.
✏️ [4] 작업 테이블 갱신
while jobs and time >= jobs[-1][0]:
requestTime, requireTime = jobs.pop()
heappush(heap,(requireTime, requestTime))- 현재 시간(
time)을 기준으로 이전에 요청된 모든 작업(jobs)을 작업 테이블(heap)에 추가한다.
✏️ [5] 작업이 남고 테이블이 빈 경우
if jobs and not heap:
requestTime, requireTime = jobs.pop()
heappush(heap,(requireTime, requestTime))- 만약 처리해야할 작업(
jobs)이 남아 있는데 작업 테이블(heap)이 비어있다면 현재 시간(time)부터 남은 작업의 요청 시간까지 공백이 존재한다는 의미이다. - 따라서 남은 작업 중 가장 먼저 요청된 작업을 작업 테이블에 추가한다.
✍ 코드
from heapq import heappop, heappush
def solution(jobs):
answer, time = 0, 0
N = len(jobs)
jobs.sort(reverse = True)
# [1] heap 초기화
requestTime, requireTime = jobs.pop()
heap = [(requireTime, requestTime)]
# [2] 최소 작업 우선 스케줄링(Shortest Job First)
while heap:
# [2-1] 가장 짧은 시간의 작업 추출
requireTime, requestTime = heappop(heap)
# [2-2] 작업 시간 및 작업 소요시간 갱신
if time < requestTime:
answer += requireTime
time = requestTime + requireTime
else:
answer += (time - requestTime) + requireTime
time += requireTime
# [2-3] 작업 테이블 갱신
while jobs and time >= jobs[-1][0]:
requestTime, requireTime = jobs.pop()
heappush(heap,(requireTime, requestTime))
# [2-4] 작업 테이블에 작업이 없지만, 작업이 남은 경우
if jobs and not heap:
requestTime, requireTime = jobs.pop()
heappush(heap,(requireTime, requestTime))
return answer//N