[Programmers] 우박수열 정적분 바로가기
📍 문제 설명
콜라츠 추측이란 로타르 콜라츠(Lothar Collatz)가 1937년에 제기한 추측으로 모든 자연수 n에 대해 다음 작업을 반복하면 항상 1로 만들 수 있다는 추측입니다.
1-1. 입력된 수가 짝수라면 2로 나눕니다.
1-2. 입력된 수가 홀수라면 3을 곱하고 1을 더합니다.
2.결과로 나온 수가 1보다 크다면 1번 작업을 반복합니다.예를 들어 주어진 수가 5 라면 5 ⇒ 16 ⇒ 8 ⇒ 4 ⇒2 ⇒ 1 이되어 총 5번만에 1이 됩니다.
수가 커졌다 작아지기를 반복하는 모습이 비구름에서 빗방울이 오르락내리락하며 우박이 되는 모습과 비슷하다고 하여 우박수 또는 우박수열로 불리기도 합니다. 현재 이 추측이 참인지 거짓인지 증명되지 않았지만 약 1해까지의 수에서 반례가 없음이 밝혀져 있습니다.
은지는 우박수열을 좌표 평면 위에 꺾은선 그래프로 나타내보려고 합니다. 초항이 K인 우박수열이 있다면, x = 0일때 y = K이고 다음 우박수는 x = 1에 표시합니다. 이런 식으로 우박수가 1이 될 때까지 점들을 찍고 인접한 점들끼리 직선으로 연결하면 다음과 같이 꺾은선 그래프를 만들 수 있습니다.
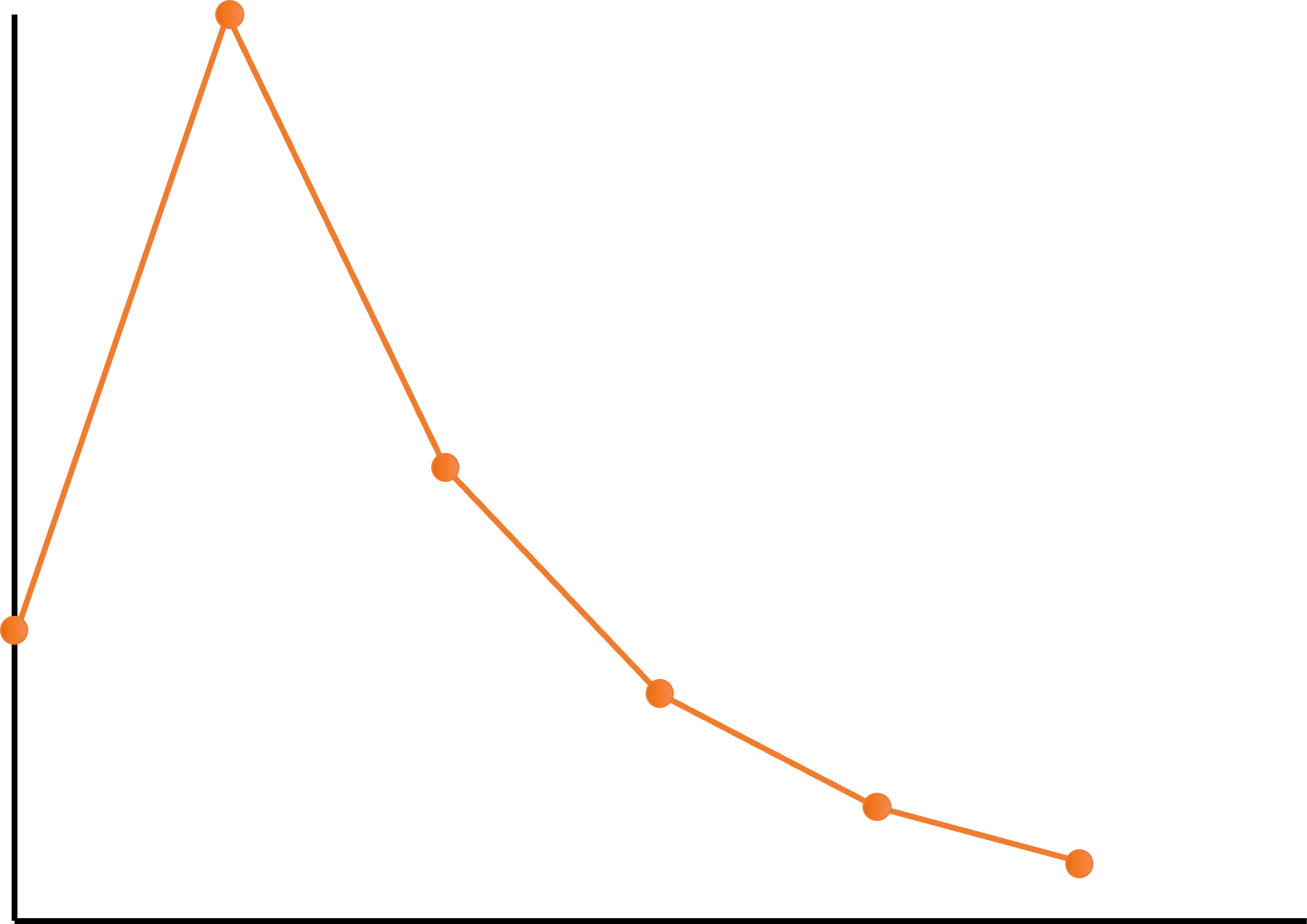
은지는 이렇게 만든 꺾은선 그래프를 정적분 해보고 싶어졌습니다. x에 대한 어떤 범위 [a, b]가 주어진다면 이 범위에 대한 정적분 결과는 꺾은선 그래프와 x = a, x = b, y = 0 으로 둘러 쌓인 공간의 면적과 같습니다. 은지는 이것을 우박수열 정적분이라고 정의하였고 다양한 구간에 대해서 우박수열 정적분을 해보려고 합니다.
단, 우박수열 그래프의 가로축 길이를 미리 알 수 없기 때문에 구간의 시작은 음이 아닌 정수, 구간의 끝은 양이 아닌 정수로 표현합니다. 이는 각각 꺾은선 그래프가 시작하는 점과 끝나는 점의 x좌표에 대한 상대적인 오프셋을 의미합니다.
예를 들어, 5를 초항으로 하는 우박수열은 5 ⇒ 16 ⇒ 8 ⇒ 4 ⇒ 2 ⇒ 1 입니다. 이를 좌표 평면으로 옮기면 (0, 5), (1, 16), (2, 8), (3, 4), (4, 2), (5, 1) 에 점이 찍히고 점들을 연결하면 꺾은선 그래프가 나옵니다. 이를 [0,0] 구간에 대해 정적분 한다면 전체 구간에 대한 정적분이며, [1,-2] 구간에 대해 정적분 한다면 1 ≤ x ≤ 3인 구간에 대한 정적분입니다.
우박수의 초항 k와, 정적분을 구하는 구간들의 목록 ranges가 주어졌을 때 정적분의 결과 목록을 return 하도록 solution을 완성해주세요. 단, 주어진 구간의 시작점이 끝점보다 커서 유효하지 않은 구간이 주어질 수 있으며 이때의 정적분 결과는 -1로 정의합니다.
📍 제한사항
- 2 ≤
k≤ 10,000 - 1 ≤
ranges의 길이 ≤ 10,000ranges의 원소는 [a, b] 형식이며 0 ≤ a < 200, -200 < b ≤ 0 입니다.
- 주어진 모든 입력에 대해 정적분의 결과는 227 을 넘지 않습니다.
- 본 문제는 정답에 실수형이 포함되는 문제입니다. 입출력 예의 소수 부분
.0이 코드 실행 버튼 클릭 후 나타나는 결괏값, 기댓값 표시와 다를 수 있습니다.
📍 입출력 예
| k | ranges | result |
|---|---|---|
| 5 | [[0,0],[0,-1],[2,-3],[3,-3]] | [33.0,31.5,0.0,-1.0] |
📍 입출력 예 설명
입출력 예 #1
5로 시작하는 우박수열은 5 ⇒ 16 ⇒ 8 ⇒ 4 ⇒ 2 ⇒ 1 입니다. 그래프에서 꺾이는 지점을 경계로 5개의 구역으로 나눠보면 각각의 구간 넓이는 10.5, 12, 6, 3, 1.5 입니다.
📍 풀이
- 정적분의 넓이를 구하는 공식은 아래와 같다.
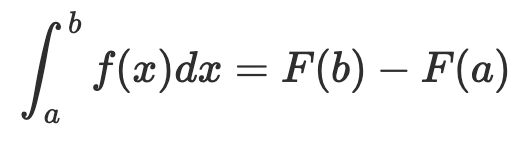
- 위 공식은
0~b까지의 정적분 값에서0~a까지의 정적분 값을 제거하는 방법으로a~b까지의 정적분 값을 구하고 있다. 0에서부터 각 지점까지의 정적분 값을 모두 알고 있으면 모든 구간의 정적분의 값을 구할 수 있다는걸 알 수 있다.
- 쉬운 이해를 돕기 이해 그래프를 통해 설명해보도록 하겠다.
k가 5로 시작할 때 생기는 우박수열의 그래프는 아래와 같다.
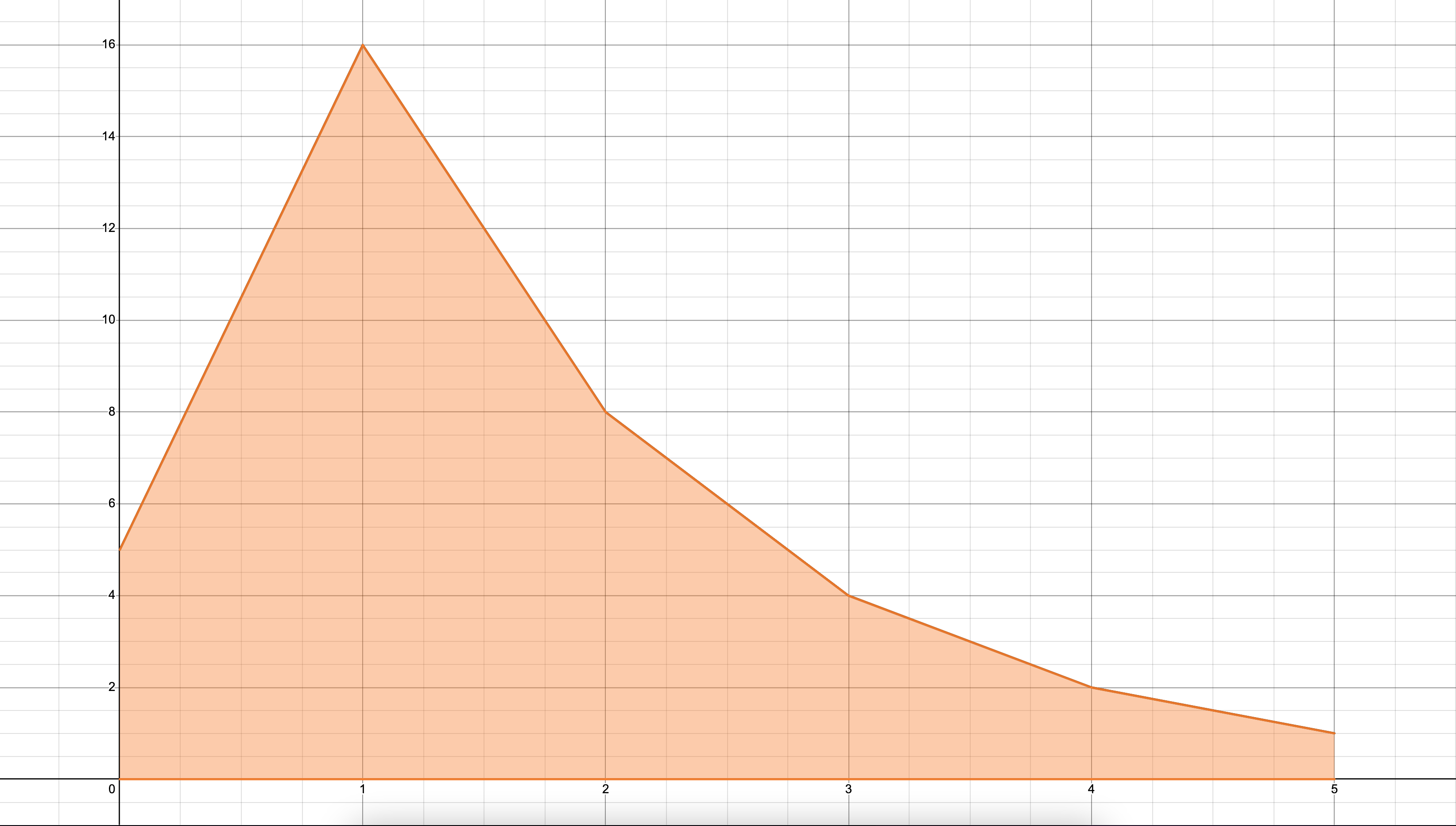
- 위 그래프의
0부터 시작해서 각 지점까지의 정적분의 값은 아래 표와 같다.
🧷 누적 정적분 값
| 정적분 범위 → (0 ~ x) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 정적분 값 → f(x) | 10.5 | 22.5 | 28.5 | 31.5 | 33 |
- 누적 정적분 값을 이용하여
2~4범위의 정적분의 값을 구하려면f(4) - f(2)의 값을 구하면 된다. - 따라서
2~4범위의 정적분의 값은31.5 - 22.5 = 9임을 알 수 있다.
🧷 0 ~ 4 범위의 정적분 넓이
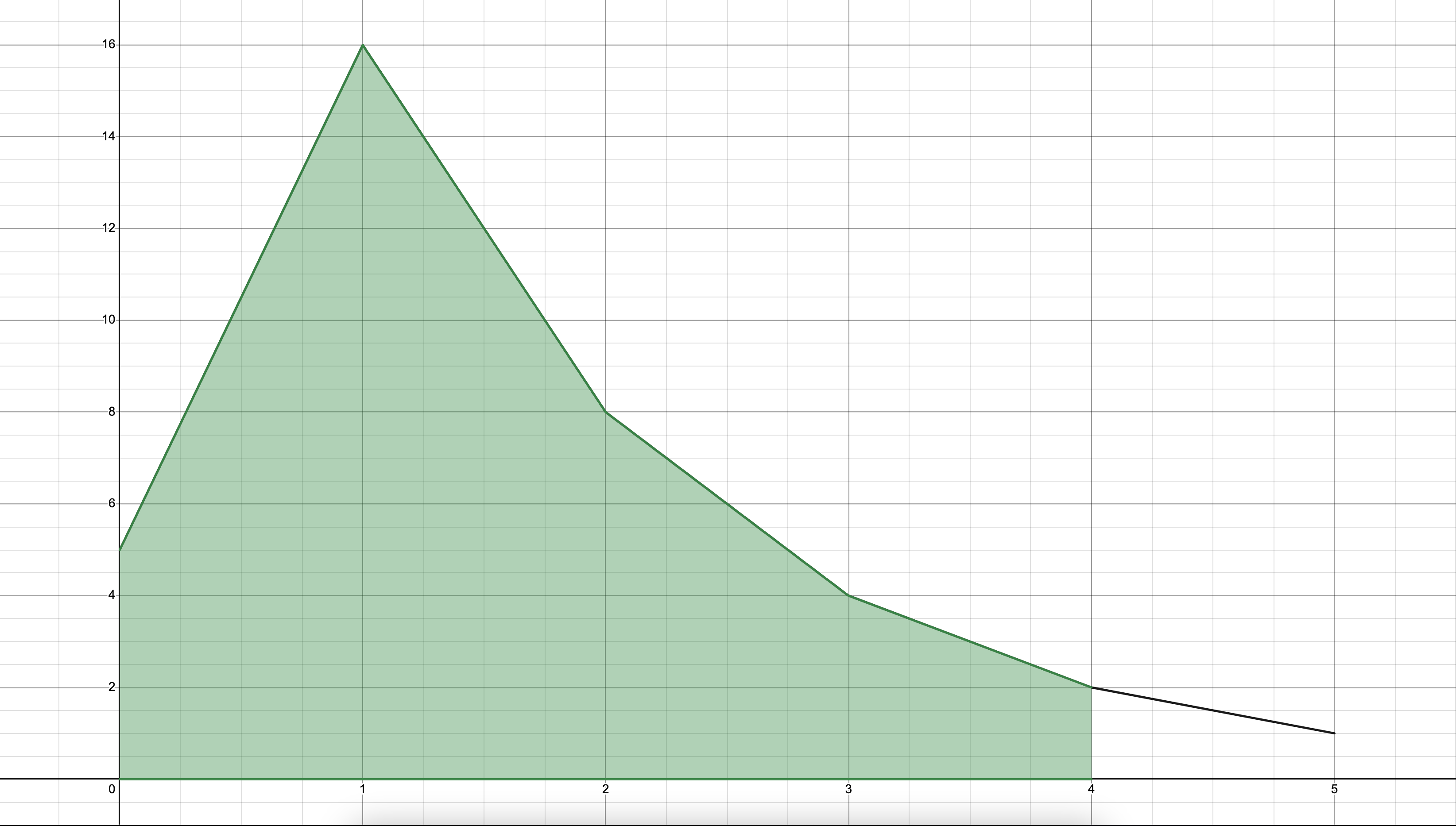
🧷 0 ~ 2 범위의 정적분 넓이
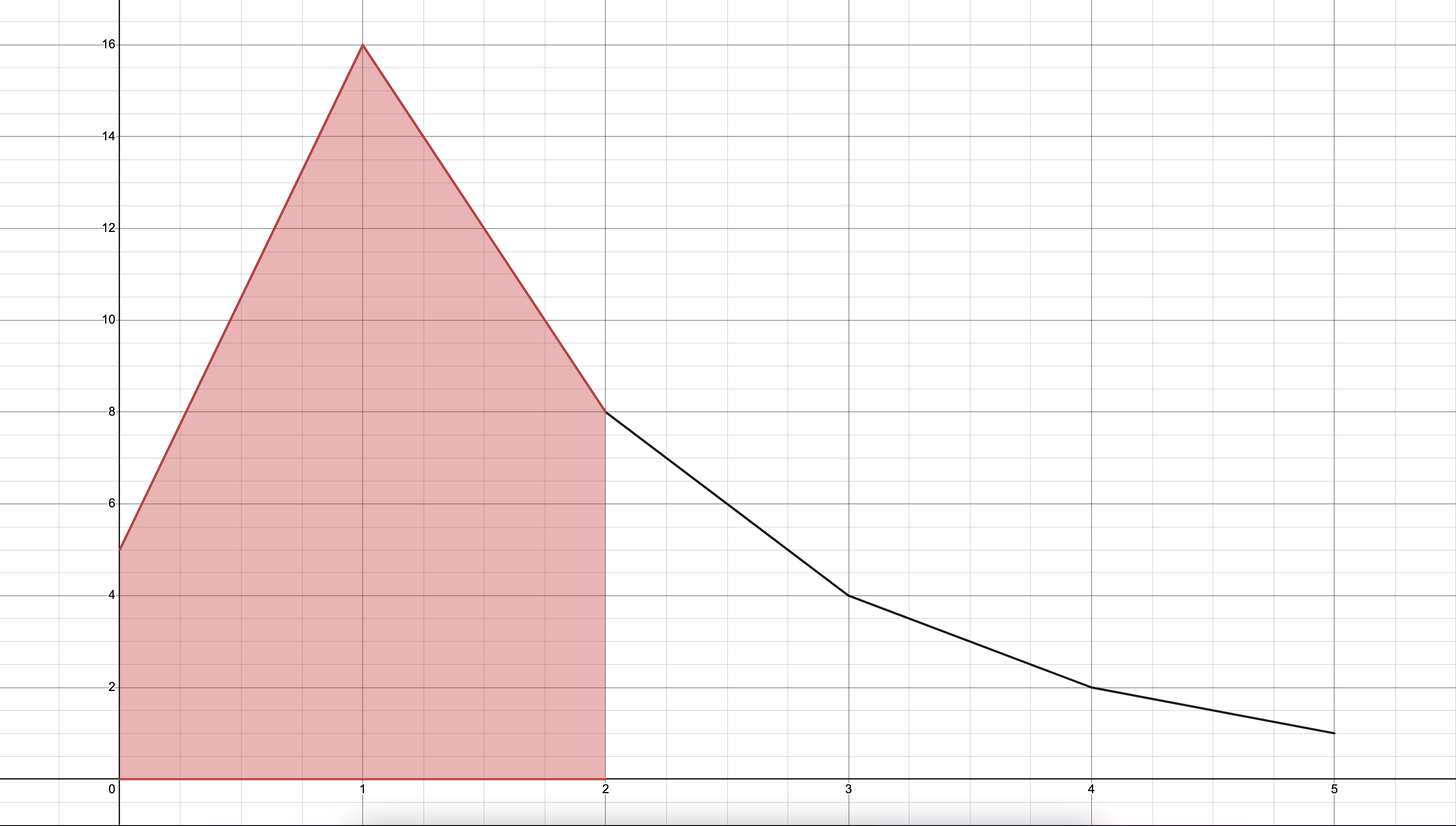
🧷 2 ~ 4 범위의 정적분 넓이
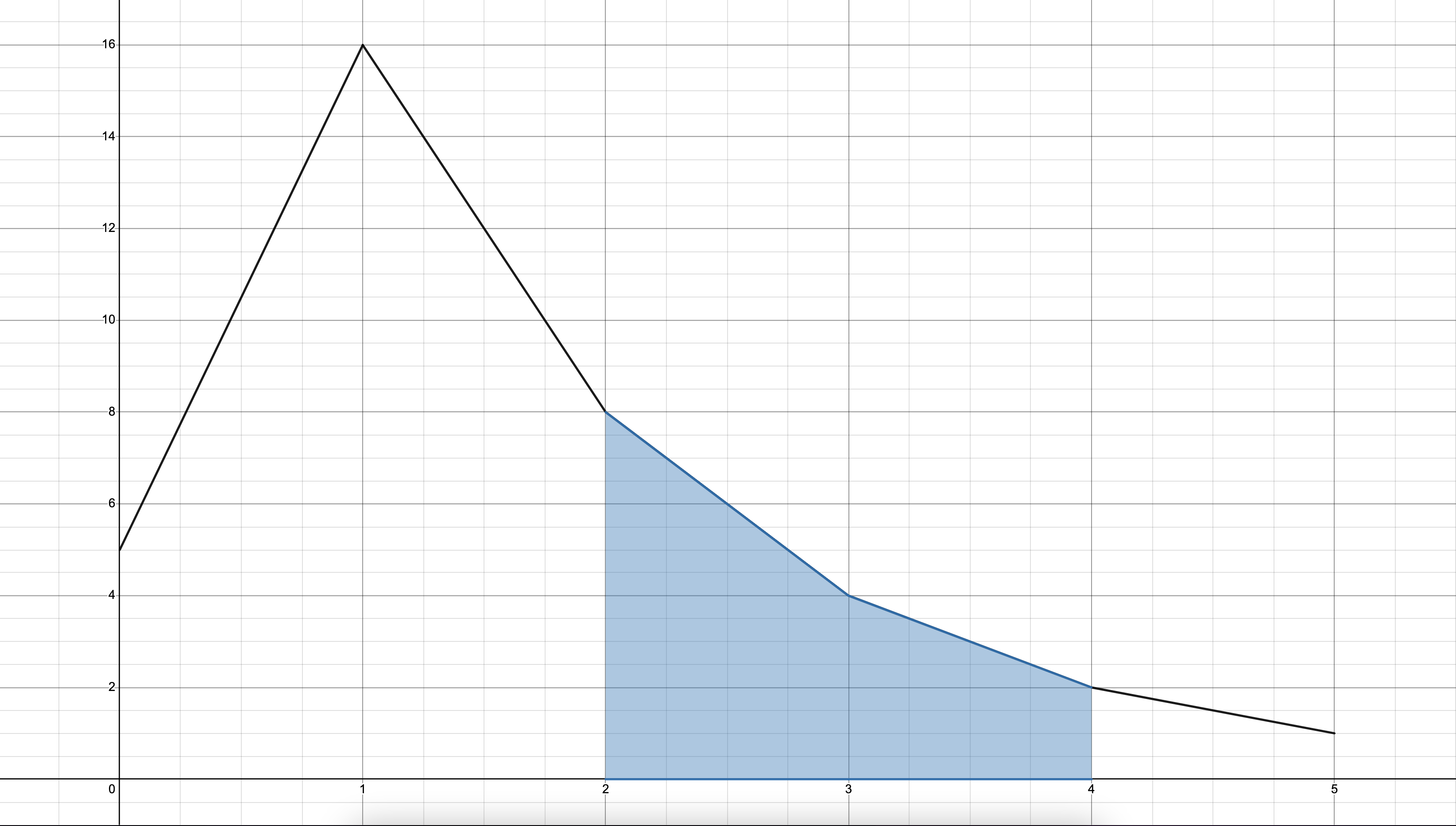
📌 문제 풀이
✏️ [1] 누적 정적분 넓이 구하기
while k != 1:
newK = (k//2) if k % 2 == 0 else (k*3+1)
minY, maxY = min(k, newK), max(k, newK)
integralArea.append(integralArea[-1] + (minY + (1/2) * (maxY - minY)))
k = newK- 현재 자연수
k를 우박 수열에 적용하여 새로운 우박수newK를 구한다. - x가 0 부터 현재 위치까지의 정적분의 넓이를
integralArea배열에 저장한다. k의 값을newK의 값으로 갱신해준다.
✏️ [2] 주어진 구간의 정적분 넓이 구하기
for y1, y2 in ranges:
if N + (y2-1) >= y1: answer.append(integralArea[y2-1] - integralArea[y1])
else: answer.append(-1)- 정적분이 가능한 범위(
y1 <= y2)라면 해당 범위의 정적분 값(integralArea[y2-1] - integralArea[y1])을answer에 추가한다. - 정적분이 불가능한 범위(
y1 > y2)라면-1을answer에 추가한다.
✍ 코드
def solution(k, ranges):
answer = []
integralArea = [0.0]
while k != 1:
# 우박 수열
newK = (k//2) if k % 2 == 0 else (k*3+1)
# 정적분 넓이
minY, maxY = min(k, newK), max(k, newK)
integralArea.append(integralArea[-1] + (minY + (1/2) * (maxY - minY)))
# 자연수 k 갱신
k = newK
N = len(integralArea) # 그래프 길이
for y1, y2 in ranges:
# 정적분이 유효한 구간
if N + (y2-1) >= y1: answer.append(integralArea[y2-1] - integralArea[y1])
# 시작점이 끝점보다 커서 유효하지 않은 구간
else: answer.append(-1)
return answer