알고리즘 - 백트랙킹

itonse·2024년 5월 28일

백트랙킹 알고리즘

자료구조 & 알고리즘

목록 보기

16/19

백트랙킹 알고리즘이란?

모든 해를 탐색하지만, 해를 찾는 도중 해가 절대 될 수 없다고 판단되면, 되돌아가서 해를 다시 찾아가는 기법
주로 DFS와 함께 사용되며, 재귀 함수를 통해 구현됩니다.
퍼즐 문제(N-Queens), 조합 문제, 부분 집합 문제, 순열 문제 등에서 사용됩니다.
특징
- 조건 확인: 각 단계에서 해가 될 수 있는지 확인하는 단계
- 가지 치기: 유망하지 않은 경로를 미리 배제하여 탐색 공간을 줄이는 단계

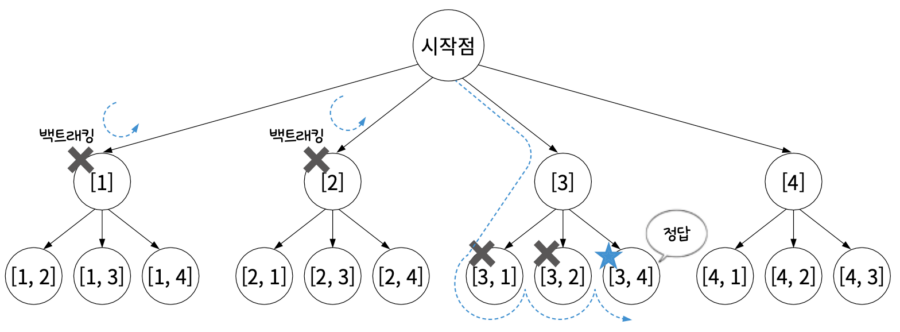
이미지 출처

시간 복잡도

문제의 성격과 탐색 공간에 크기에 따라 차이가 납니다.

1. N-Queens 문제

N-Queens 문제는 NxN 체스보드 위에 N개의 퀸을 서로 공격하지 않게 배치하는 문제입니다. 백트래킹을 사용하여 모든 가능한 배치를 탐색합니다.

가능한 상태 수: 각 퀸은 N개의 위치 중 하나에 놓일 수 있으므로, 최악의 경우 모든 퀸을 배치하는 경우의 수는 N! (N 팩토리얼)입니다.
시간 복잡도: O(n!)

2. 순열 생성

주어진 n개의 원소로 모든 순열을 생성하는 문제입니다. 예를 들어, {1, 2, 3}의 순열을 생성하는 문제입니다.

가능한 상태 수: n개의 원소로 만들 수 있는 순열의 수는 n! 입니다.
시간 복잡도: O(n!)

3. 조합 생성

주어진 n개의 원소에서 k개의 원소를 선택하는 모든 조합을 생성하는 문제입니다. 예를 들어, {1, 2, 3, 4}에서 2개의 원소를 선택하는 모든 조합을 생성하는 문제입니다.

가능한 상태 수: n개의 원소에서 k개의 원소를 선택하는 경우의 수는 C(n, k) = n! / (k!(n-k)!)입니다.
시간 복잡도: O(C(n, k))

4. 부분 집합 생성

주어진 n개의 원소로 만들 수 있는 모든 부분 집합을 생성하는 문제입니다.

가능한 상태 수: n개의 원소로 만들 수 있는 부분 집합의 수는 2^n입니다.
시간 복잡도: O(2^n)

예시 코드

기본 코드

void backtrack(상태 current) {
    // (1) 해가 되는 조건 확인
    if (해가 되는 조건) { 
        해를 저장하거나 출력
        return;
    }
    
    // (2) 가능한 모든 선택지를 탐색
    for (각 선택지 in 가능한 선택지들) {
        // (3) 조건 확인 
        if (조건 확인(선택지)) { 
            선택지를 현재 상태에 추가   // (4) 상태 업데이트
            backtrack(업데이트된 상태)   // (5) 다음 단계로 재귀 호출
            선택지를 현재 상태에서 제거 (백트랙킹)    // (6) 백트랙킹: 재귀가 끝나면 선택지 제거(상태 복귀)
        }  // (7) 조건을 만족하지 않으면 이 선택지는 가지치기 (Pruning)
    }
}

문제: 주어진 배열에서 합이 5가 되는 모든 부분 집합 찾기 (조합 문제)

백트래킹을 이용해서 각 단계에서 조건 확인과 가지치기를 통해 불필요한 탐색을 줄여 효율적으로 해를 찾기

import java.util.*;

class Solution {
    public static void main(String[] args) {
        int[] nums = {1, 2, 3, 4, 5};
        int target = 5;
        List<List<Integer>> results = new ArrayList<>();
        backtrack(nums, target, 0, new ArrayList<>(), results);
    }
    
    public static void backtrack(int[] nums, int target, int start, List<Integer> current, List<List<Integer>> results) {
        if (target == 0) {  // (1) 해가 되는 조건: 목표 합에 도달
            results.add(new ArrayList<>(current));  // 해를 저장
            return;
        }
        
        // (2) 가능한 모든 선택지를 탐색
        for (int i = start; i < nums.length; i++) { 
            // (3) 조건 확인: 현재 숫자가 남은 목표보다 작거나 같은지 확인
            if (nums[i] <= target) {  
                current.add(nums[i]);  // (4) 상태 업데이트
                backtrack(nums, target - nums[i], i + 1, current, results);  // (5) 다음 단계로 재귀 호출
                current.remove(current.size() - 1);  // (6) 백트래킹: 선택지 제거
            }  // (7) 조건을 만족하지 않으면 가지치기: 현재 숫자가 남은 목표보다 크면 넘어감
        }
    }
}