자료구조 & 알고리즘

가장 직관적이고 구현하기 쉬운 탐색 방법현재 정점과 연결된 정점들을 하나씩 갈 수 있는지 검사하고, 특정 정점으로 갈 수 있다면 그 정점에 가서 같은 행위를 반복한다.같은 정점을 다시 방문하지 않아도 정점에 방문했다는 것을 표시해준다.재귀 함수를 통해 구현한다.장점:

이진 탐색 알고리즘은 정렬된 배열에서 특정 값을 빠르게 찾기 위해 사용됩니다.탐색 과정에서 배열의 중간값과 찾고자 하는 값을 비교하여 매 단계에서 탐색 범위를 절반으로 줄이는 방식으로 작동합니다.이 알고리즘의 효율성은 대체로 O(logn)의 시간 복잡도를 갖습니다.re

재귀 함수는 실행 과정에서 자기 자신을 호출하는 함수문제를 더 작은 문제로 나눌 수 있는 경우복잡한 문제를 더 작고 관리하기 쉬운 부분으로 나눌 수 있다. 반복문의 중첩이 복잡하거나 예측하기 어려운 경우중첩 반복문을 사용하는 대신 재귀 함수를 사용하면 코드의 가독성을

지금 당장의 최선의 선택지만을 골라가며 해를 도출해나가는 방법을 채택한알고리즘지금의 선택이 앞으로 남은 선택들에 거떤 영향을 끼칠지 고려하지 않는다.당장 눈 앞의 이익만을 좇는다.일반적인 상황에서 그리디 알고리즘은 최적의 해를 보장할 수 없을 때가 많다.그리디 알고리즘

삽입, 삭제, 검색의 시간 복잡도가 전부 O(1)이다.HashMap<String, Integer> map = new HashMap<>();map.put("초록", 1);map.put("파랑", 2);System.out.println(map.get("초록"))

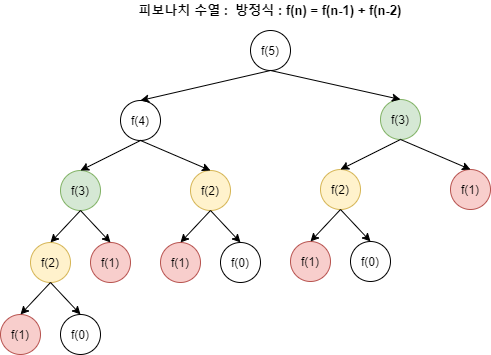
다이나믹 프로그래밍은 복잡한 문제를 여러 개의 간단한 하위 문제로 나누어 해결하는 알고리즘 설계 기법입니다. 각 하위 문제의 해답을 저장하고 재사용함으로써, 전체 문제를 효율적으로 해결할 수 있습니다. 이 방법은 특히 반복되는 계산을 많이 요구하는 문제에 효과적이며,

연속된메모리 공간 사용\-> index를 통해 각 요소에 접근 가능, 탐색에 필요한 시간복잡도는 O(1)삽입이나 삭제의 경우에는 다른 요소들을 이동(shift)해야 하므로 O(n)의 시간복잡도를 가짐크기가 고정적 (컴파일시 정적으로 메모리 할당)정리: 추가, 삭제 연산

처음부터 끝까지 순차적으로 탐색하며, 각 턴에서 현재 턴의 데이터들 중 가장 작은 값을 찾습니다.현재 턴의 맨 앞 데이터는 이미 정렬이 완료된 상태로 간주합니다. 따라서 다음 턴에서는 그 다음 데이터부터 마지막 데이터까지 동일한 과정을 반복합니다.첫 번째 요소는 이미

퀵 정렬은 분할 정복(Divide and Conquer) 방식을 사용하여 정렬합니다. 평균적으로 매우 빠른 성능을 보여주며, 평균 시간 복잡도는 𝑂(nlogn)입니다.기준 값 선택 (Pivot Selection): 배열에서 하나의 요소를 선택하여 기준 값(pivot)

합병 정렬이라고도 부르며, 분할 정복 방법을 통해 구현됩니다.시간 복잡도는 평균 O(NlogN)퀵정렬과는 반대로 안정 정렬에 속합니다.\-> 퀵정렬은 불안정 정렬: 동일한 값의 원소들의 상대적인 순서가 정렬 과정에서 유지되지 않을 수 있음퀵정렬은 우선 피벗을 통해 정렬

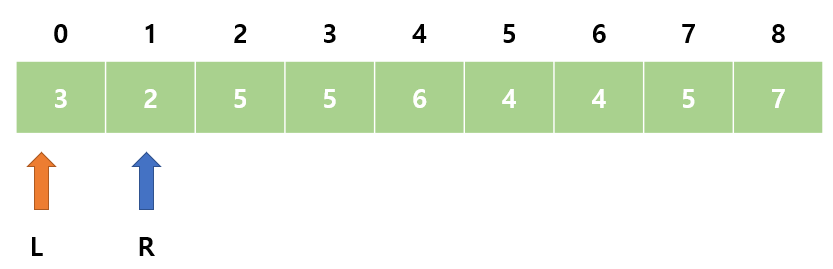
투포인터는 List에 순차적으로 접근해야 할 때 두 개의 점의 위치를 기록하면서 처리하는 알고리즘 입니다.1차원 배열에서 각자 다른 원소를 가리키고 있는 2개의 포인터를 조작해가면서 원하는 값을 찾을 때 까지 탐색합니다.두 개의 포인터 start와 end는 현재 부분

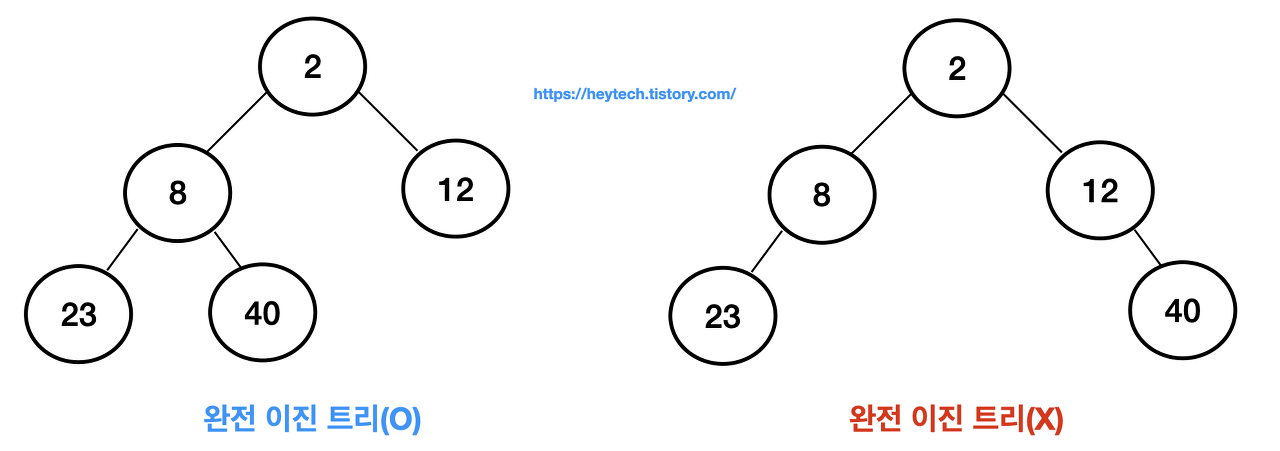
힙(heap)은 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 설계된 완전 이진트리를 기본으로 한 자료구조 입니다.완전 이진트리 (마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있는 트리)중복값 허용최댓값, 최솟값을 빠리게 찾기 용이종류최대 힙(max hea

큐는 FIFO(선입선출) 구조 형식의 자료구조입니다.ex) 줄 선 순서대로 입장(여기서 <자료형> 을 생략하면 어떤 자료형이든 넣을 수 있습니다.)큐는 LinkedList를 사용한다는 것이 특징인데, 이는 ArrayList보다 삽입/삭제 연산에서 유리하다는 장점이

스택의 삭제(pop) 연산의 시간복잡도는 맨 위의 원소를 제거하는 것 이기 때문에 O(1) 입니다. 검색의 경우 full scan을 해서 특정 데이터를 찾는 것 이므로 O(n)의 시간복잡도를 가집니다.큐의 삭제(Dequeue) 연산의 시간복잡도는 가장 먼저 들어온 원소

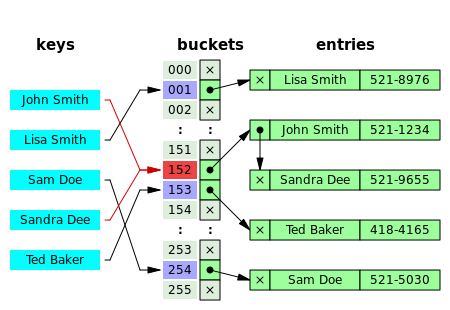
해시 관련 용어 정리 해시 함수 (Hash Function): 임의의 데이터를 일정한 크기의 해시값으로 변환하는 함수. 해시 (Hash): 해시 함수의 결과물이며, 저장소에서 값(value)과 매칭되어 저장된다 해시 테이블 (Hash Table): key-valu

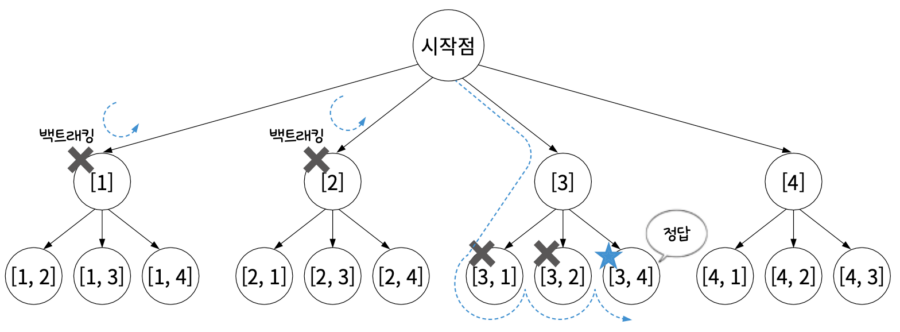
모든 해를 탐색하지만, 해를 찾는 도중 해가 절대 될 수 없다고 판단되면, 되돌아가서 해를 다시 찾아가는 기법주로 DFS와 함께 사용되며, 재귀 함수를 통해 구현됩니다.퍼즐 문제(N-Queens), 조합 문제, 부분 집합 문제, 순열 문제 등에서 사용됩니다.특징조건 확

서로 다른 n개에서 r개를 뽑아서 정렬하는 경우의 수DFS 이용시간 복잡도: O(P(n, r)) = O(n! / (n-r)!)순열 예제: 5P3n개의 숫자 중에서 r개의 수를 순서 없이 뽑는 경우의 수백트랙킹 이용시간 복잡도: O(C(n, r)) = O(n! / (r!

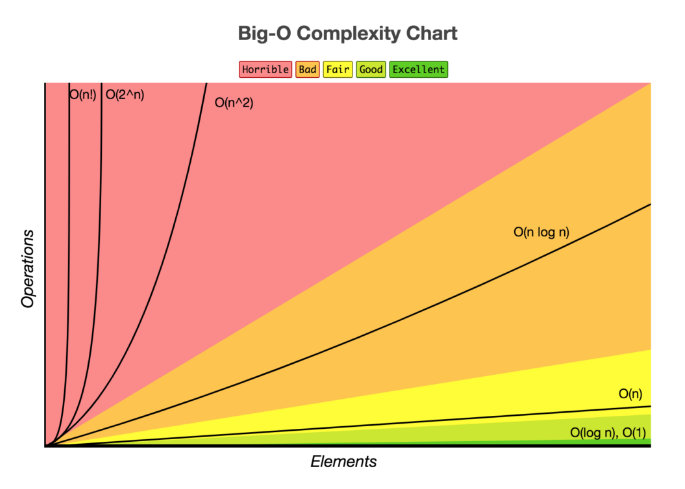
복잡도는 알고리즘의 성능과 효율성을 나타내는 척도입니다. 주로 시간 복잡도와 공간 복잡도로 나눌 수 있으며, 각 알고리즘이 주어진 특정 크기의 입력(N)을 기준으로 수행 시간 혹은 사용 공간이 얼마나 되는지를 객관적으로 비교할 수 있는 기준을 제시합니다.시간 복잡도:

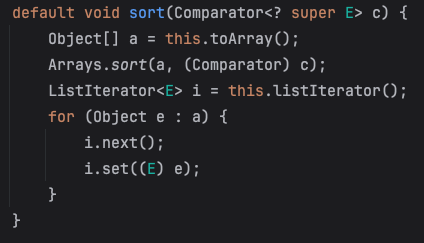
위의 코드는 Comparator 인터페이스의 compare 메서드를 구현한 람다 표현식입니다. 이 람다 표현식은 o1과 o2 두 객체를 비교하여 정렬하게됩니다.list.sort((o1, o2) -> 비교식(비교 결과 값) ) 호출List.sort() 메서드가 호출되어