정렬(3) 병합정렬(Merge Sort)

병합정렬 개념

• 합병정렬이라고도 부르며, 분할 정복 방법을 통해 구현됩니다.
  -> 배열을 재귀적으로 분할하고, 분할된 부분 배열을 정렬한 후 다시 합병하여 전체 배열을 정렬합니다

• 시간 복잡도는 평균 O(NlogN)

병합 정렬의 과정

(1)분할 단계

• 배열을 두 개의 부분 배열로 나눕니다.
  -> 이 과정을 부분 배열의 크기가 1이 될 때까지 반복합니다.

(2)정복 단계

• 부분 배열이 더 이상 나눌 수 없을 때, 부분 배열을 정렬된 상태로 합병합니다.
• 두 부분 배열을 비교하여 더 작은 값을 앞에 두고 병합을 진행합니다.

(3)병합 단계

• 정렬된 부분 배열들을 병합하여 최종적으로 하나의 정렬된 배열을 만듭니다.

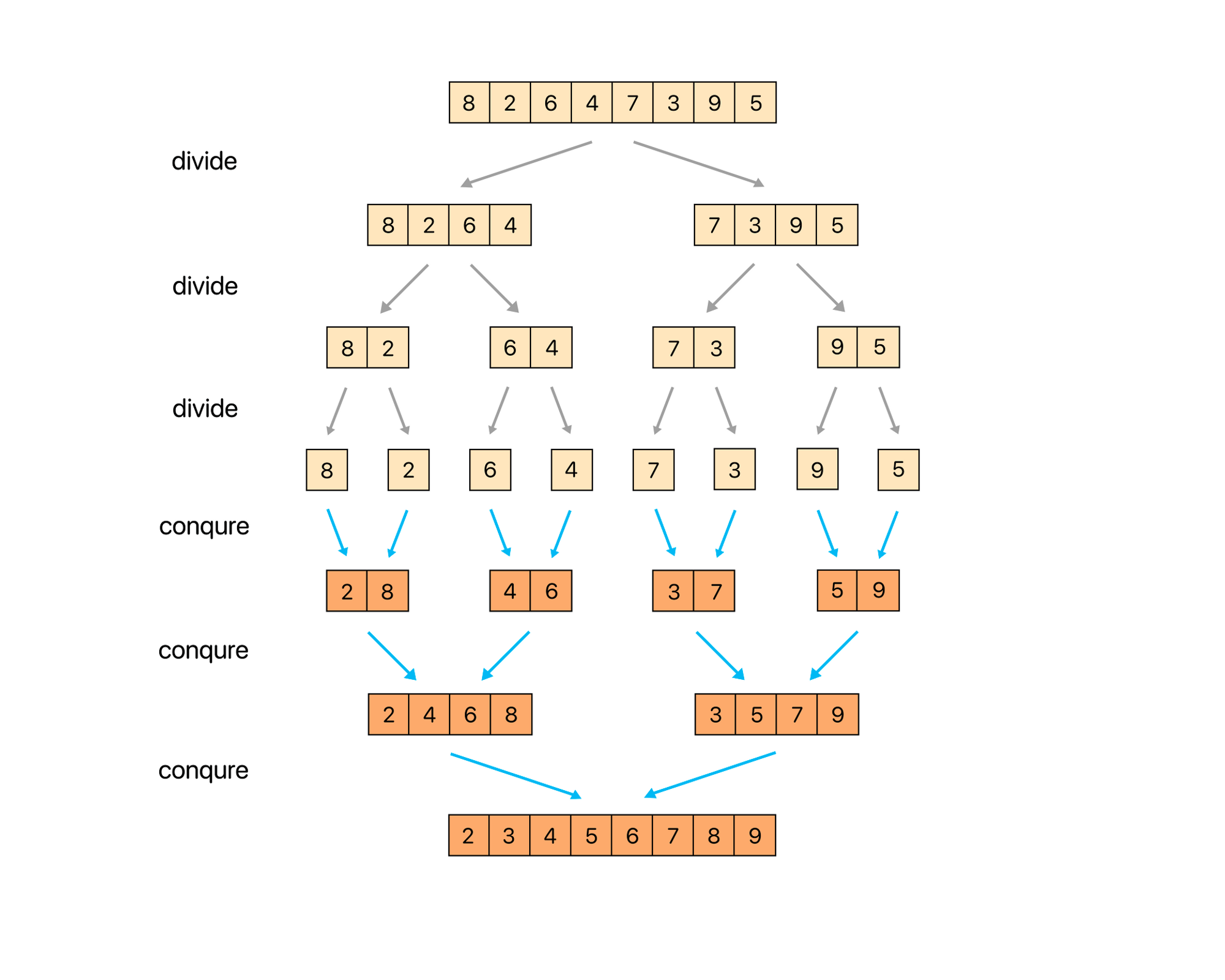
이미지 출처

병합 방식

• 각 부분리스트의 첫번째 원소부터 순차적으로 비교하면서 병합합니다.
  -> 병합 과정에서 각 부분 리스트는 정렬된 상태입니다.

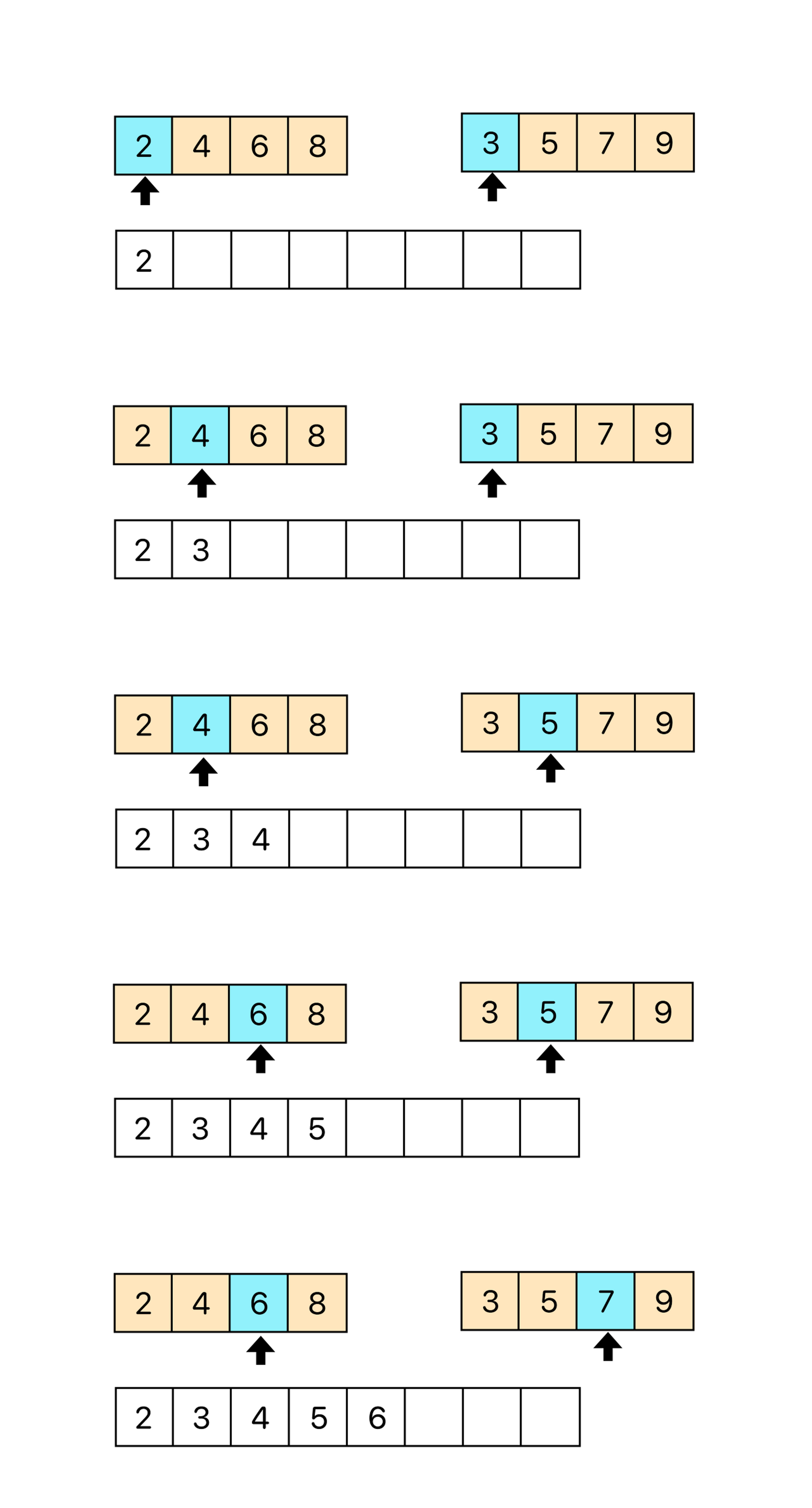
이미지 출처

병합정렬 코드

public class MergeSort {
	// 메인 함수
    public static void main(String[] args) {
        int[] array = {12, 11, 13, 5, 6, 7};

        // 병합 정렬 호출
        mergeSort(array, 0, array.length - 1);
    }
    
    // 병합 정렬 함수
    public static void mergeSort(int[] array, int left, int right) {
        if (left < right) {
            int middle = (left + right) / 2;

            // 배열의 왼쪽 절반 정렬
            mergeSort(array, left, middle);
            // 배열의 오른쪽 절반 정렬
            mergeSort(array, middle + 1, right);

            // 두 절반 배열을 병합
            merge(array, left, middle, right);
        }
    }

    // 두 개의 정렬된 배열을 병합하는 함수
    public static void merge(int[] array, int left, int middle, int right) {
        int n1 = middle - left + 1;
        int n2 = right - middle;

        int[] leftArray = new int[n1];
        int[] rightArray = new int[n2];

        // 왼쪽, 오른쪽 배열에 데이터 복사
        for (int i = 0; i < n1; ++i) leftArray[i] = array[left + i];
        for (int j = 0; j < n2; ++j) rightArray[j] = array[middle + 1 + j];

        int i = 0, j = 0;
        int k = left;

        // 병합 작업
        while (i < n1 && j < n2) {
            if (leftArray[i] <= rightArray[j]) {
                array[k] = leftArray[i];
                i++;
            } else {
                array[k] = rightArray[j];
                j++;
            }
            k++;
        }

        // 남은 요소 병합
        while (i < n1) array[k++] = leftArray[i++];
        while (j < n2) array[k++] = rightArray[j++];
    }
}

병합정렬의 장단점

장점

• 항상 두 부분리스트로 쪼개어 들어가기 때문에 최악의 경우에도 O(NlogN)으로 유지가 됩니다.
• 퀵정렬과는 반대로 안정 정렬에 속합니다.
  -> 퀵정렬은 불안정 정렬: 동일한 값의 원소들의 상대적인 순서가 정렬 과정에서 유지되지 않을 수 있음

단점

• 정렬 과정에서 추가적인 보조 배열 공간을 사용하기 때문에 메모리 사용량이 많습니다.
• 보조 배열에서 원본 배열로 복사하는 과정은 많은 시간을 소비하게 되므로, 데이터가 많을 경우
  상대적으로 많은 시간이 소요될 수 있습니다.

---

ref.
https://github.com/gyoogle/tech-interview-for-developer/blob/master/Algorithm/MergeSort.md
https://emptyhead.oopy.io/4d0d7147-ca5d-4de1-9c4e-f140a9fe57f2