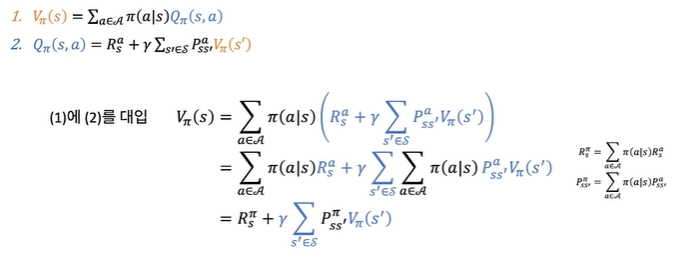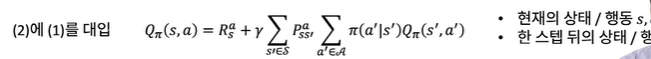강화학습 강의 필기(1강-강화학습 소개, 2강- 가치기반 강화학습의 풀이법)

Kiwoong Park·2022년 3월 13일
강화학습
1

1강 강화학습 소개

강화학습의 분류

강화학습 에이전트의 환경에 대한 모델 유무에 따른 분류

강화학습

  • (모델 없는, Model free) 강화학습 (일반적인 강화학습)
    • 가치기반 강화학습(가치함수를 직접적으로 추산, value based)
    • 정책기반 강화학습(가치함수 대신 곧바로 정책함수를 최적화, policy based)
    • Actor-Critic(가치기반, 정책기반의 각 장점을 살려)
  • 모델 기반 강화학습(Model based)

강화학습에 활용되는 수식

조건부 확률(conditional probability)

Ex) 전체 원룸 매물 중 70%가 전자렌지가 있고, 40%가 TV가 있다고 하자. 또한 전체 원룸 중 90%가 적어도 둘 중 하나는 가지고 있다고 할 때, 전자렌지가 없는 원룸 중, TV도 없을 확률은?

P(X)P(X)=전체 원룸 중 전자렌지가 없을 확률 = 0.3
P(Y)P(Y)=전체 원룸 중 TV가 없을 확률 = 0.6
P(Y∩X)P(Y \cap X)=전체 원룸 중 둘다 없을 확률 = 1-0.9 = 0.1
구하고 싶은 값, P(Y∣X)P(Y|X) = P(Y∩X)P(X)\frac{P(Y \cap X)}{P(X)} = 0.1/0.3 = 1/3

기댓값을 근사적으로 계산하는 방법: Monte-Carlo 기법

주사위 눈의 기댓값을 계산할 때, 만약에 우리가 각 눈이 나올 확률을 모른다면?

  • 기댓값이란, 일어날 수 있는 사건들의 확률*개별결과값의 합계이므로 주사위를 무한히 던져서 나온 값들을 평균하면 거의 기댓값과 같아질 수 있음.

조건부 기댓값(Conditional expectation)

E(Y∣X=x)=∑ip(Y=yi∣X=x)yiE(Y|X=x) = \sum_{i}p(Y=y_i|X=x)y_i

로 정의되면 즉, xx에 대한 함수임

X, Y는 random variable 이며 Y에 대한 함수가 아니고 X에 대한 함수임.

2강 가치기반 강화학습의 풀이법

Ch 01. 마르코프 결정과정(Markov Decision Process)

  • 강화학습 문제 : Markov Decision Process 를 가정하고 풀이
    • 강화학습 문제를 기술하는 "수학적인 표현방법!"
    • MDP를 최대한 쉽게 이해하기 몇 가지 전 단계
      • 마르코프 과정(Markov Process) 혹은 마르코프 연쇄(Markov chain)으로도 불림
      • 마르코프 보상 과정(MRP)
      • 마르코프 결정 과정(MDP)
  • 풀이 기법
    • 환경에 대해서 알 때 : DP(Dynamic Programming)
      • (상대적으로)문제를 해결하기 쉬움
      • 매우 효율적임
      • 비현실적임
    • 환경에 대해서 모를 떄 : MC, TD
      • (DP에 비해) 효율성이 떨어짐
      • 현실적인 문제의 상황에 적용 가능

마르코프 특성(Markov property)

"어떤 상태 sts_t는 Markov하다의 정의 :

P(st+1∣st)=P(st+1∣st,st−1,...,s0)P(s_{t+1}|s_t) = P(s_{t+1}|s_t,s_{t-1}, ..., s_0)

현재 상태 sts_t를 알면, 역사를 아는 것과 동일한 수준으로 미래 상태를 추론할 수 있다.
즉, 미래의 상태는 과거와 무관하게 현재의 상태만으로 결정된다.

마르코프 과정(Markov process)

마르코프 과정(마르코프 연쇄)는 <S,P><S,P>인 튜플이다.

  • SS은 (유한한) 상태의 집합
  • PP는 상태 천이 행렬

상태 천이 행렬(State Transition matrix)

현재 상태 ss에서 s′s'로 이동할 확률 Pss′P_{ss'}

Pss′=P(St+1=s′∣S=s)P_{ss'}=P(S_{t+1}=s'|S=s)

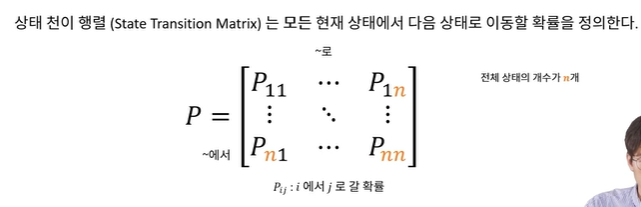
각 로우(=가로)의 요소의 합은 항상 1.0이 되어야 함.

마르코프 보상 과정

마르코프 보상 과정(MRP)는 <S,P,R,γ><S,P,R,\gamma>인 튜플이다.

  • SS은 (유한한) 상태의 집합
  • PP는 상태 천이 행렬
  • RR는 보상 함수, R:S→RR:S \rarr \mathbb{R} ~ 확률적/결정적일 수 있음
  • γ\gamma는 감가율, γ∈[0,1]\gamma \in [0,1] ~ 0이상 1이하의 실수 중 하나

리턴(GtG_t)

리턴 GtG_t는 현재시점 tt부터 전체 미래에 대한 "감가"된 보상의 합

Gt=Rt+1+γRt+2+γ2Rt+3+...=∑τ∞γτ−1Rt=Rt+1+γGt+1(recursive표현)G_t = R_{t+1}+\gamma R_{t+2}+\gamma ^2 R_{t+3} + ... = \sum_{\tau }^{\infin}\gamma ^{\tau -1}R_t \\ = R_{t+1} + \gamma G_{t+1} (recursive 표현)

RtR_t는 확률변수로 아직 하나의 결정된 값은 아님 즉, GtG_t 리턴의 경우도 하나로 결정된 값이 아닌 확률변수

보상 함수 Rt+1R_{t+1}은 상태 sts_t를 떠날 때의 보상값을 의미

항상 에피소드가 끝나는 경우에는 γ=1.0\gamma=1.0을 사용하기도 한다.

가치함수(Value function)

가치함수 V(s)V(s)는 현재 상태 ss에서 미래의 "감가된 보상의 합(=리턴(GtG_t))"의 기댓값. 리턴은 확률 변수이기 때문에 기대값을 구하여 하나의 정해진 스칼라 값으로 바꿔줌!

V(s)=E[Gt∣St=s]V(s) = E[G_t|S_t=s]

즉, 현재 상태에서 미래의 기대 리턴은 얼마인가?

마르코프 결정과정(Markov decision process:MDP)

마르코프 결정 과정(MDP)는 <S,A,P,R,γ><S,A,P,R,\gamma>인 튜플이다.

  • SS은 (유한한) 상태의 집합
  • AA는 (유한한) 행동의 집합
  • PP는 상태 천이 행렬, Pss′a=P[St+1=s′∣St=s,At=a]P^a_{ss'}=P[S_{t+1}=s'|S_t=s, A_t=a] ~ 더 이상 매트릭스로 표현 불가능! AA 축이 추가된 3d 구조로 표현해야 됨.
  • RR는 보상 함수, R:S×A→RR:S \times A \rarr \mathbb{R} ~ 확률적/결정적일 수 있음
  • γ\gamma는 감가율, γ∈[0,1]\gamma \in [0,1] ~ 0이상 1이하의 실수 중 하나

비로소, 환경에 행동을 가함으로써 미래의 상태와, 보상을 바꿀 수 있게 됨!

정책 함수 (Policy function)

정책함수 π\pi는 현재 상태에서 수행 할 행동의 확률 분포

π(a∣s)=P(At=a∣St=s)\pi (a|s) = P(A_t=a|S_t=s)

MDP의 가치함수

상태 가치함수 : Vπ(s)=Eπ[Gt∣St=s]V_\pi(s)=E_\pi [G_t|S_t=s]
현재 tt 상태 ss에서 정책 π\pi를 따른다면 얻을 미래 가치의 감가 총합

행동 가치함수 : Qπ(s)=Eπ[Gt∣St=s,At=a]Q_\pi(s)=E_\pi [G_t|S_t=s, A_t=a]
현재 tt 상태 ss에서 aa라는 행동을 취한 후, 정책 π\pi를 따른다면 얻을 미래 가치의 감가 총합

상태가치 함수 VV와 행동 가치함수 QQ의 관계

행동 가치함수로 상태 가치함수 표현하기
현재 상태 ss에서 각각의 행동 aa를 할 확률이 π(a∣s)\pi(a|s)이므로, 각 상태와 행동에 대한 가치 Qπ(s,a)Q_\pi(s,a)를 π(a∣s)\pi(a|s)로 평균을 내면 현재 상태의 가치 Vπ(s)V_\pi(s)가 됨.

상태 가치함수로 행동 가치함수 표현하기

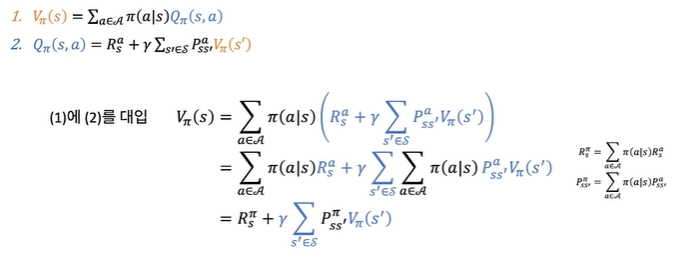
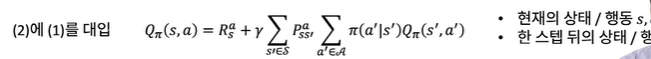
Bellman (expectation) equation의 행렬표현과 직접해

v=Rπ+γPπvv=(I−γPπ)−1Rπv = R^\pi + \gamma P^\pi v \\ v = (I-\gamma P^\pi)^{-1}R^\pi

최적 가치 함수 (Optimal Value Function)

최적 가치함수 (혹은 그것을 만드는 정책함수 π\pi를 찾았을 때) MDP를 '풀었다'라고 표현.

최적 상태 가치 함수

V∗(s)V^*(s): 존재하는 모든 정책들 중에 모든 상태 ss에서 가장 높은 Vπ(s)V_\pi(s)를 만드는 π\pi를 적용했을 때 얻는 Vπ(s)V_\pi(s), V∗(s)=mπaxVπ(s)V^*(s)=\underset{\pi}maxV_\pi(s)

최적 행동 가치 함수

Q∗(s,a)Q^*(s,a): 존재하는 모든 정책들 중에 모든 상태/행동 조합 (s,a)(s,a)에서 가장 높은 Qπ(s,a)Q_\pi(s,a)를 만드는 π\pi를 적용했을 때 얻는 Qπ(s,a)Q_\pi(s,a), V∗(s)=mπaxQπ(s,a)V^*(s)=\underset{\pi}maxQ_\pi(s,a)

최적 정책(Optimal policy)

정책함수 π\pi간의 대소관계를 다음과 같이 정의한다.

π′≥π,↔Vπ′(s)≥Vπ(s),∀s∈S\pi' \ge \pi, \leftrightarrow V_{\pi'}(s) \ge V_\pi(s), \forall s \in S

최적 정책 정리(Optimal policy theorem)

어떠한 MDP에 대해서도 다음이 성립한다.

  • 최적 정책 π∗\pi^*가 존재하며, 모든 존재하는 정책 π\pi에 대하여 π∗≥π\pi^* \ge \pi를 만족한다.(최적 정책의 존재성)
  • 최적 정책들은 π∗\pi^* 최적 상태 가치함수를 성취한다. 즉, Vπ∗(s)=V∗(s)V_{\pi^*}(s) = V^*(s)이다.
  • 최적 정책들은 π∗\pi^* 최적 행동 가치함수를 성취한다. 즉, Qπ∗(s,a)=Q∗(s,a)Q_{\pi^*}(s,a) = Q^*(s,a)이다.

1) 최적 정책이 유일하게 존재하는 것은 아님
2) 최적 정책을 찾으면 최적 가치함수를 찾을 수 있음.

최적 가치 함수 중 하나를 찾는 방법

흥미로운 항등식: Bellman (expectation) equation

V(s)=E[Gt∣St=s]=E[Rt+1+γRt+2+γ2Rt+3+...∣St=s]=E[Rt+1+γ(Rt+2+γRt+3+...)∣St=s](4)=E[Rt+1+γGt+1∣St=s](5)=E[Rt+1+γV(St+1)∣St=s]V(s) = E[G_t|S_t=s] \\ = E[R_{t+1}+\gamma R_{t+2}+\gamma ^2 R_{t+3} + ... |S_t=s] \\ = E[R_{t+1}+\gamma (R_{t+2}+\gamma R_{t+3} + ... ) |S_t=s] \\ (4) = E[R_{t+1} + \gamma G_{t+1} |S_t=s] \\ (5) = E[R_{t+1} + \gamma V(S_{t+1})|S_t=s]

(4) →\rarr (5): E[A]=E[E[A]]E[A] = E[E[A]]를 활용.

E[Rt+1+γGt+1∣St=s]=E[Rt+1∣St=s]+E[γGt+1∣St=s]=E[Rt+1∣St=s]+γE[Gt+1∣St=s]=E[Rt+1∣St=s]+γV(St+1)=E[Rt+1∣St=s]+γE[V(St+1)∣St=s]=E[Rt+1+γV(St+1)∣St=s]E[R_{t+1} + \gamma G_{t+1} |S_t=s] = E[R_{t+1}|S_t=s] + E[\gamma G_{t+1} |S_t=s]\\ = E[R_{t+1}|S_t=s] + \gamma E[G_{t+1} |S_t=s] \\ = E[R_{t+1}|S_t=s] + \gamma V(S_{t+1}) \\ = E[R_{t+1}|S_t=s] + \gamma E[V(S_{t+1})|S_t=s] \\ = E[R_{t+1} + \gamma V(S_{t+1})|S_t=s]

보상함수, R(s)R(s)가 결정적이라고 가정시,

V(s)=R(s)+γ∑s′∈St+1Pss′V(s′)V(s) = R(s) + \gamma \sum_{s'\in S_{t+1}}P_{ss'}V(s')

벨만 방정식은 선형 연립방정식을 활용해 표현 가능!

v=R+γPvv=R+\gamma P v

vv 는 모든 상태의 value function 값을 담은 벡터. v∈Rnv \in \mathbb{R}^n, R\mathbb{R}은 실수 공간, n^n은 n×1n\times 1의 1차원의 벡터
RR 는 모든 상태의 reward function 값을 담은 벡터. R∈RnR \in \mathbb{R}^n
PP 는 상태 전이 매트릭스. P∈Rn×nP \in \mathbb{R}^{n\times n}
(보통, 소문자 영어는 벡터를, 대문자 영어는 매트릭스를 표현)

벨만 기대 방정식의 풀이법

v=R+γPv(I−γP)v=Rv=(I−γP)−1Rv = R + \gamma Pv \\ (I-\gamma P)v = R \\ v = (I-\gamma P)^{-1}R
  • 벨만 기대 방정식은 선형 방정식이기 때문에 직접적으로 해를 구하는 것이 가능
  • 하지만 n이 커질 수록 직접적으로 푸는 것이 어려워짐
    • DP, MC, TD를 이용해 문제를 풀 수 있음.

마르코프 결정과정 (MDP)

  • 마르코프 결정과정은 MRP에 행동을 추가한 확률 과정
  • MDP는 <S,A,P,R,γ><S, A, P, R, \gamma>인 튜플이다.
    • AA는 (유한한) 행동의 집합
    • PP는 상태 전이 확률, Pss′a=P[St+1=s′∣St=s,At=a]P_{ss'}^a=P[S_{t+1}=s'|S_t=s, A_t=a]
      • 더이상 매트릭스로 표현 불가능! 3d 구조로 표현해야 함.
    • RR 는 보상함수, R:S×A→RR:S \times A \rarr \mathbb{R} 확률적/결정적일 수 있음

환경에 행동을 가함으로써 미래의 상태와, 보상을 바꿀 수 있게 됨!

정책함수 (policy function)

정책함수 π\pi는 현재 상태에서 수행할 행동의 확률분포

π(a∣s)=P[At=a∣St=s]\pi (a|s) = P[A_t=a|S_t=s]

강화학습 에이전트는 현재상태 sts_t를 활용하여, 현재의 행동 ata_t를 결정한다.
sts_t를 아는 것이 과거를 아는 것과 동일하다는 Markov 특성을 가정하였으므로, 현재 상태만을 가지고 의사결정을 해도 충분함

MDP, MRP와 MP의 관계

MDP <S,A,P,R,γ><S,A,P,R,\gamma >와 정책 π\pi가 결정 됐을 때,

  • So,S1,S2,...S_o, S_1, S_2, ...는 마르코프 과정이다.
  • So,R1,S1,R2,S2,...S_o, R_1, S_1, R_2, S_2, ...는 마르코프 보상 과정 <S,Pπ,Rπ,γ><S,P^{\pi}, R^{\pi},\gamma >이다.
PSS′π=∑a∈Aπ(a∣s)Pss′aRSπ=∑a∈Aπ(a∣s)RsaP^{\pi}_{SS'} = \sum_{a\in A} \pi(a|s)P_{ss'}^a \\ R^{\pi}_S = \sum_{a\in A} \pi(a|s)R_s^a

좋은 π\pi를 가지고 있다면, 최대한 많은 이득을 얻는 것이 가능하다!

MDP의 가치함수

상태 가치함수(State value function): Vπ(s)=Eπ[Gt∣St=s]V_\pi (s) = E_\pi [G_t|S_t=s]

현재 tt 상태 ss에서 정책 π\pi를 따른다면 얻을 미래의 가치의 감가 총합

행동 가치함수(상태-행동 가치함수라고도 함, State-action value function): Qπ(s)=Eπ[Gt∣St=s,At=a]Q_\pi(s) = E_\pi [G_t|S_t=s, A_t=a]

현재 tt 상태 ss에서 a라는 행동을 취한 후, 정책 π\pi를 따른다면 얻을 미래의 가치의 감가 총합.

상태가치 함수 VV와 행동 가치함수 QQ의 관계

(1). 행동 가치함수 →\rarr 상태 가치함수

Vπ(s)=∑a∈Aπ(a∣s)Qπ(s,a)V_\pi(s) = \sum_{a\in A} \pi(a|s)Q_\pi(s,a)

현재 상태 ss에서 각각의 행동 aa를 할 확률이 π(a∣s)\pi(a|s)이므로, 각 상태와 행동에 대한 가치 Qπ(s,a)Q_\pi(s,a)를 π(a∣s)\pi(a|s)로 평균을 내면 현재 상태의 가치 Vπ(s)V_\pi(s)가 된다.

(2). 상태 가치함수 →\rarr 행동 가치함수

Qπ(s,a)=Rsa+γ∑s′∈SPss′aVπ(s′)Q_\pi(s,a) = R_s^a + \gamma \sum_{s'\in S}P^a_{ss'}V_\pi(s')

현재 ss상태에서 aa를 행동하면, RsaR_s^a 만큼의 보상을 받고 확률적으로 어떤 s′s'들에 도달하게 된다. 각 도달한 s′s'에서 각각의 가치는 Vπ(s′)V_\pi(s')이니, 다음에 기대적으로 얻을 가치는 각각의 s′s'에 대한 확률 Pss′aP^a_{ss'}과 가치를 Vpi(s′)V_{pi}(s') 활용해 평균을 낸 값이다. 그 후 γ\gamma 만큼 감가한다.

(1)에 (2)를 대입

Vπ(s)=∑a∈Aπ(a∣s)(Rsa+γ∑s′∈SPss′aVπ(s′))=∑a∈Aπ(a∣s)Rsa+γ∑s′∈S∑a∈Aπ(a∣s)Pss′aVπ(s′)=Rsπ+γ∑s′∈SPss′πVπ(s′)V_\pi(s) = \sum_{a\in A}\pi(a|s)(R_s^a+\gamma \sum_{s'\in S}P^a_{ss'}V_\pi(s')) \\ = \sum_{a\in A}\pi(a|s)R_s^a + \gamma \sum_{s'\in S}\sum_{a\in A}\pi(a|s)P^a_{ss'}V_\pi(s') \\ = R_s^\pi + \gamma \sum_{s'\in S}P^\pi_{ss'}V_\pi(s')

(2)에 (1)를 대입

Qπ(s,a)=Rsa+γ∑s′∈SPss′a∑a∈Aπ(a′∣s′)Qπ(s′,a′)Q_\pi(s,a) = R_s^a + \gamma \sum_{s'\in S}P^a_{ss'}\sum_{a\in A} \pi(a'|s')Q_\pi(s',a')
  • 현재의 상태 / 행동 →s,a\rarr s, a
  • 한 스텝 뒤의 상태 / 행동 →s′,a′\rarr s', a'

Bellman (expectation) equation의 행렬표현과 직접해

v=Rπ+γPπvv=(I−γPπ)−1Rπv = R^\pi + \gamma P^\pi v \\ v = (I-\gamma P^\pi)^{-1}R^\pi

Value function, Vπ(s)V_\pi(s)를 계산한다면, 최적의 π\pi는 어떻게 결정할 것인가? 를 정리하는 질문들

좋은 π\pi를 가지고 있다면, 최대한 많은 이득을 얻는 것이 가능하다!

  • 무엇이 좋은 π\pi의 기준일까?
  • 무엇이 최적의 π\pi를 결정지을까?

최적 가치 함수(Optimal Value Function)

최적 상태 가치함수: V∗(s)=maxπVπ(s)V^*(s)=\underset{\pi}{max}V_\pi(s)

최적 상태 가치함수: 존재하는 모든 정책들 중에 모든 상태 ss에서 가장 높은 Vπ(s)V_\pi(s)를 만드는 π\pi를 적용했을 때 얻는 Vπ(s)V_\pi(s)

최적 행동 가치함수: Q∗(s,a)=maxπQπ(s,a)Q^*(s,a)=\underset{\pi}{max}Q_\pi(s,a)

최적 행동 가치함수: 존재하는 모든 정책들 중에 모든 상태/행동 조합 (s,a)(s,a)에서 가장 높은 Qπ(s,a)Q_\pi(s,a)를 만드는 π\pi를 적용했을 때 얻는 Qπ(s,a)Q_\pi(s,a)

최적 가치함수 (혹은 그것을 만드는 π\pi를 찾았을 때) MDP를 '풀었다'고 라고 표현

최적 정책(Optimal policy)

정책함수 π\pi간의 대소관계를 다음과 같이 정의한다.

π′≥π↔Vπ′(s),∀s∈S\pi' \ge \pi \leftrightarrow V_{\pi'}(s), \forall s \in S

실제 정책의 수학적 대소관계가 아님.

최적 정책 정리(Optimal policy theorem)
어떠한 MDP에 대해서도 아래의 내용이 성립한다.

  • 최적 정책 π∗\pi^*가 존재하며, 모든 존재하는 정책 π\pi에 대하여 π′≥π\pi' \ge \pi를 만족한다. (최적 정책의 존재성)
  • 최적 정책들은 π∗\pi^* 최적 상태 가치함수를 성취한다. 즉, Vπ∗(s)=V∗(s)V_{\pi^*}(s) = V^*(s)이다.
  • 최적 정책들은 π∗\pi^* 최적 행동 가치함수를 성취한다. 즉, Qπ∗(s,a)=Q∗(s,a)Q_{\pi^*}(s,a) = Q^*(s,a)이다.

1) 최적 정책이 유일하게 존재하는 것은 아님.
2) 최적 정책을 찾으면 최적 가치함수를 찾을 수 있음.

최적 가치함수 중 하나를 찾는 방법

만약 최적 가치함수 Q∗(s,a)=maxπQπ(s,a)Q^*(s,a)=\underset{\pi}{max} Q_\pi(s,a)를 안다면,
(존재하는 여러가지 최적 정책 중 하나를) 찾는 방법:

π∗(a∣s)={1,  if  a=argmaxa∈AQ∗(s,a)0,  otherwise\pi^*(a|s) = \begin{cases} 1,\; if \; a = \underset{a \in A}{argmax}Q^*(s,a) \\ 0,\; otherwise \end{cases} \\

이때, argmaxQ∗(s,a){argmax}Q^*(s,a) 는 Q∗(s,a)Q^*(s,a) 들 중에서 Q∗(s,a)Q^*(s,a)를 최대화하는 a를 찾아서 내놓아라

Bellman 최적 방정식(Bellman Optimality Equation, BOE)

(1)V∗(s)=∑a∈Aπ∗(a∣s)Q∗(s,a)=maxa∈AQ∗(s,a)(1) V^*(s) = \sum_{a \in A}\pi^*(a|s)Q^*(s,a) \\ = \underset{a \in A}{max}Q^*(s,a)
(2)Q∗(s,a)=Rsa+γ∑s′∈SPss′aV∗(s′)(2) Q^*(s,a) = R_s^a + \gamma \sum_{s'\in S}P^a_{ss'}V^*(s')

(1)에 (2)를 대입

V∗(s)=maxa∈A(Rsπ+γ∑s′∈SPss′aV∗(s′))V^*(s) = \underset{a \in A}{max}(R_s^\pi + \gamma \sum_{s'\in S}P^a_{ss'}V^*(s'))

(2)에 (1)를 대입

Q∗(s,a)=Rsa+γ∑s′∈SPss′amaxa′∈AQ∗(s′,a′)Q^*(s,a) = R_s^a + \gamma \sum_{s'\in S}P^a_{ss'}\underset{a' \in A}{max}Q^*(s',a')

Bellman optimality equation, BOE 직접해(일반해)는 존재하지 않음

  • BOE는 선형방정식이 아님.
  • BOE는 일반해가 존재하지 않음.
  • 대신 반복적인 알고리즘을 통해서 해를 계산할 수 있음.
    • Policy iteration, Policy evaluation
    • Value iteration
    • Q-Learning
    • SARSA
    • ...
profile
Kiwoong Park
You matter, never give up
이전 포스트

N차 정규화

다음 포스트

영어 회화 준비 (feat. Naver Clova)

0개의 댓글