Leetcode : Letter Combinations of a Phone Number

digits 가 들어오면 해당 딕셔너리 안에서 가능한 조합들을 모두 꺼내는 알고리즘 같다. 내용을 보면 전화 키패드에서 사용되는 숫자와 문자의 매핑을 사용해야 하는 백트래킹 문제로 보여진다. 문제는 가능한 모든 문자 조합을 반환하라고 요청하고 있다.

1. 먼저, 숫자와 문자를 매핑하는 딕셔너리를 생성한다. 이 딕셔너리는 각 숫자를 문자들의 리스트로 매핑하며, 이것은 전화 키패드에 기반한 매핑이다.
2. 두 번째로, 백트래킹 함수를 정의한다. 이 함수는 현재까지 구성된 조합과 다음으로 처리해야 하는 숫자 위치를 인자로 받는다.
3. 백트래킹 함수 내에서, 만약 현재까지 구성된 조합이 입력된 숫자 문자열의 길이와 같다면, 이 조합은 완전하다는 것을 의미한다. 따라서 이 조합을 결과 리스트에 추가하고, 백트래킹 함수를 종료한다.
4. 만약 조합이 아직 완전하지 않다면, 다음 숫자에 해당하는 모든 문자를 반복하며, 각 문자를 현재까지의 조합에 추가하고, 다음 숫자 위치로 백트래킹 함수를 재귀 호출한다.
5. 이 백트래킹 함수를 입력된 숫자 문자열의 첫 번째 숫자 위치에서 호출하면, 함수는 가능한 모든 조합을 결과 리스트에 추가하며, 이 리스트를 최종 결과로 반환한다.

class Solution:
    def letterCombinations(self, digits: str) -> List[str]:
        if not digits:
            return []

        phone = {
            "2": "abc",
            "3": "def",
            "4": "ghi",
            "5": "jkl",
            "6": "mno",
            "7": "pqrs",
            "8": "tuv",
            "9": "wxyz"
        }

        def backtrack(combination, next_digits):
            if len(next_digits) == 0:
                output.append(combination)

            else:
                for letter in phone[next_digits[0]]:
                    backtrack(combination + letter, next_digits[1:])

        output = []
        backtrack("", digits)
        return output

class Solution:
    def letterCombinations(self, digits: str) -> List[str]:
        def dfs(index, path):
            if len(path) == len(digits):
                result.append(path)
                return
            for i in range(index, len(digits)):
                for j in dic[digits[i]]:
                    dfs(i + 1, path + j)

        if not digits:
            return []

        dic = {
            "2": "abc",
            "3": "def",
            "4": "ghi",
            "5": "jkl",
            "6": "mno",
            "7": "pqrs",
            "8": "tuv",
            "9": "wxyz"
        }

        result = []
        dfs(0, "")

        return result

Leetcode : Permutations

“Permutations (순열) : 주어진 원소들을 사용하여 만들 수 있는 모든 가능한 순서” 라고 한다. Input 으로 nums 라는 배열이 넘어오면 인덱스들로 가능한 모든 조합을 꺼내는 알고리즘을 구현하는 문제로 보여진다. 이 문제 에 백트래킹 알고리즘을 적용하여 모든 가능한 상태 공간을 탐색할 수 있을 것 같다.

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        # 결과를 저장할 리스트
        result = []

        # 주어진 리스트의 순열을 찾는 함수
        def find_permutations(nums, current_permutation):
            # 만약 주어진 리스트가 비었다면, 현재의 순열을 결과에 추가
            if not nums:
                result.append(current_permutation)
                return

            # 주어진 리스트의 모든 숫자에 대해 순열 찾기
            for i in range(len(nums)):
                # 숫자를 선택하고, 선택하지 않은 숫자들에 대해 순열 찾기
                remaining_nums = nums[:i] + nums[i+1:]
                new_permutation = current_permutation + [nums[i]]
                find_permutations(remaining_nums, new_permutation)

        # 주어진 숫자들에 대해 순열 찾기 시작
        find_permutations(nums, [])

        # 결과 반환
        return result

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        def dfs(path):
            if len(path) == len(nums):
                result.append(path[:])
                return

            for i in range(len(nums)):
                if nums[i] in path:
                    continue
                dfs(path + [nums[i]])

        result = []
        dfs([])
        return result

Leetcode : Reconstruct Itinerary

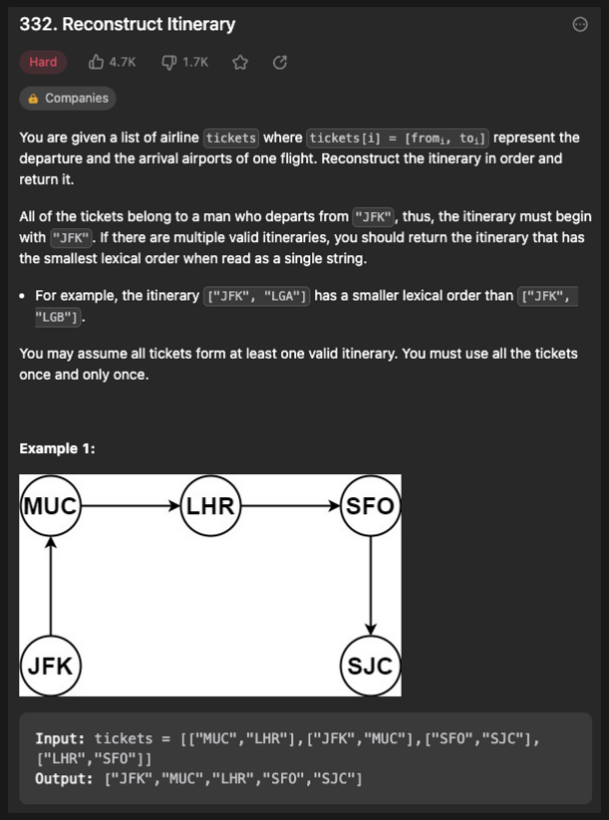
일정을 재구성하는 문제이다. from 과 to 가 적힌 티켓들이 전달되면 첫 from 은 JFK 로 고정하고 이후 티켓들을 돌면서 from 과 to 가 연결될 수 있도록 일정이 들어간 배열을 반환하는 문제로 보여진다. 만약 같은 출발지인데 다른 도착지가 있는 경우 lexical order 에 따라서 다음 목적지를 결정한다.

from collections import defaultdict
class Solution:
    def findItinerary(self, tickets: List[List[str]]) -> List[str]:
        # 그래프를 만들어. 공항을 키로하고 출발과 도착을 값으로 가지는 딕셔너리로
        # 도착지들은 우선순위 큐로 관리 (lexical)
        graph = defaultdict(list)

        # reverse 를 써서 뒤집어 두면 나중에 pop()으로 해결 가능
        for depart, arrive in sorted(tickets, reverse=True):
            graph[depart].append(arrive)

        route = []

        def dfs(airport):
            while graph[airport]:
                dfs(graph[airport].pop())
            route.append(airport)

        dfs("JFK")
        return route[::-1]

from collections import defaultdict
class Solution:
    def findItinerary(self, tickets: List[List[str]]) -> List[str]:
        graph = defaultdict(list)
        for a, b in sorted(tickets):
            graph[a].append(b)

        route = []

        def visit(city):
            while graph[city]:
                next_city = graph[city].pop(0)
                visit(next_city)
            route.append(city)

        visit("JFK")
        return route[::-1]

Leetcode : Network Delay Time

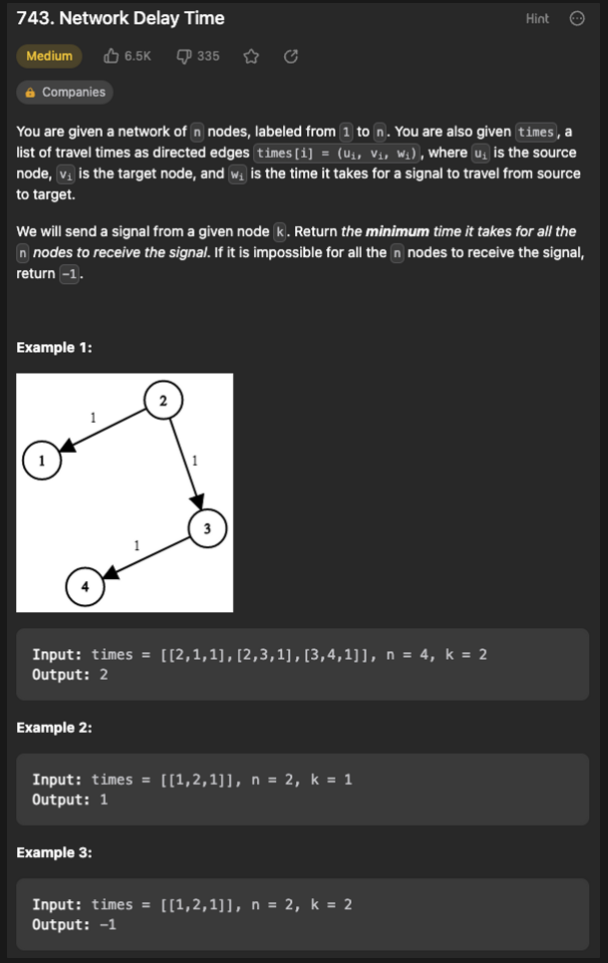
주어진 n 노드의 네트워크 내에서 특정 노드에서 신호를 보냈을 때 모든 노드가 신호를 수신하는 데 걸리는 최소 시간을 찾는 문제로 보인다.

# Network Delay Time : 다익스트라 알고리즘
import collections
import heapq

class Solution:
    def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
        # 그래프 구성
        graph = collections.defaultdict(list)
        for u, v, w in times:
            graph[u].append((v, w))

        # 큐 변수: [(소요 시간, 정점)]
        Q = [(0, k)]
        dist = collections.defaultdict(int)

        # 우선순위 큐 최소값 기준으로 정점까지 최단 경로 삽입
        while Q:
            time, node = heapq.heappop(Q)
            if node not in dist:
                dist[node] = time
                for v, w in graph[node]:
                    alt = time + w
                    heapq.heappush(Q, (alt, v))

        # 모든 노드의 최단 경로 존재 여부 판별
        if len(dist) == n:
            return max(dist.values())
        return -1