• 수학 안에서도 좀 더 구체적으로 그래프를 설명하자면, 그래프 이론에서 객체의 일부 쌍들이 연관되어 있는 개체 집합 구조를 말한다.
• 일반적으로는 정점(노드)과 간선(엣지)으로 이루어진 자료구조를 의미한다.
• 간선의 방향 유무에 따라서 단방향 그래프와 무방향 그래프(또는 양방향)로 나뉜다.
• 그래프의 표현은 크게 인접 행렬 그래프와 인접 리스트 그래프로 나눌 수 있다.
• 그래프 순회란, 그래프 탐색이라고도 불리우며 그래프의 각 정점을 방문하는 과정을 말한다.
• 탐색 기법에는, 너비 우선 탐색, 깊이 우선 탐색, 다익스트라, 플로이드 와샬 등이 있다.

BFS 탐색 (Breadth First Search)

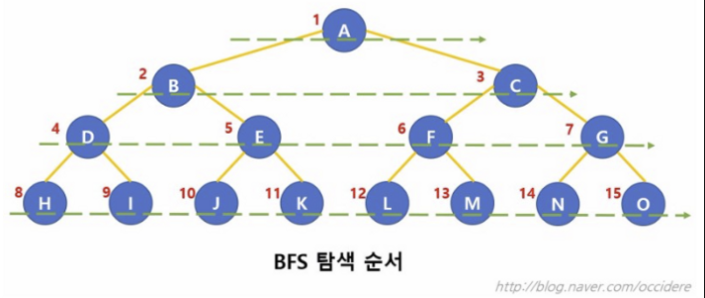
• 현재 정점과 연결된 점들에 대해 우선적으로 넓게 탐색
• 큐를 이용해 구현

DFS 탐색 (Depth First Search)

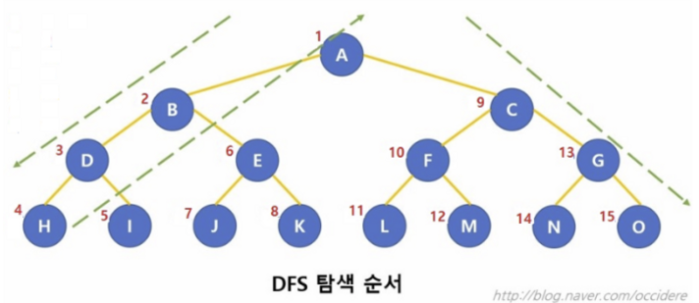
• 현재 정점에서 연결된 정점을 하나 골라 파고들 수 있는 최대한 깊게 파고 들어가며 탐색
• 스택을 이용해서 구현

예시 코드

# 그래프 알고리즘
graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}

visited = set() # 방문한 노드를 저장할 집합

###########################
# DFS (깊이 우선 탐색) - 재귀 함수
def dfs_recursive(node):
    if node not in visited:
        print(node, end=' ')
        visited.add(node)
        for neighbor in graph[node]:
            dfs_recursive(neighbor)

# 시작 노드 설정 및 함수 호출
start_node = 'A'
dfs_recursive(start_node)

###########################
# DFS (깊이 우선 탐색) - 스택 사용
def dfs_iterative(start_node):
    stack = [start_node]

    while stack:
        node = stack.pop()
        if node not in visited:
            print(node, end=' ')
            visited.add(node)
            stack.extend(reversed(graph[node]))

# 시작 노드 설정 및 함수 호출
start_node = 'A'
dfs_iterative(start_node)

###########################
# BFS (너비 우선 탐색) - 큐를 이용한 반복 구조로 구현
from collections import deque
def bfs_iterative(start_node):
    queue = deque([start_node]) # BFS 큐 초기화

    while queue:
        node = queue.popleft()
        if node not in visited:
            print(node, end=' ')
            visited.add(node)
            queue.extend(graph[node])

# 시작 노드 설정 및 함수 호출
start_node = 'A'
bfs_iterative(start_node)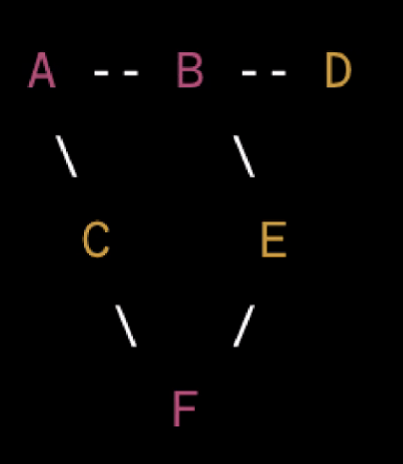

Resource:

[그래프] 쉽게 쓴 그래프 알고리즘 기초 (2018.03.06 수정완료)