
leetcode : Maximum Depth of Binary Tree
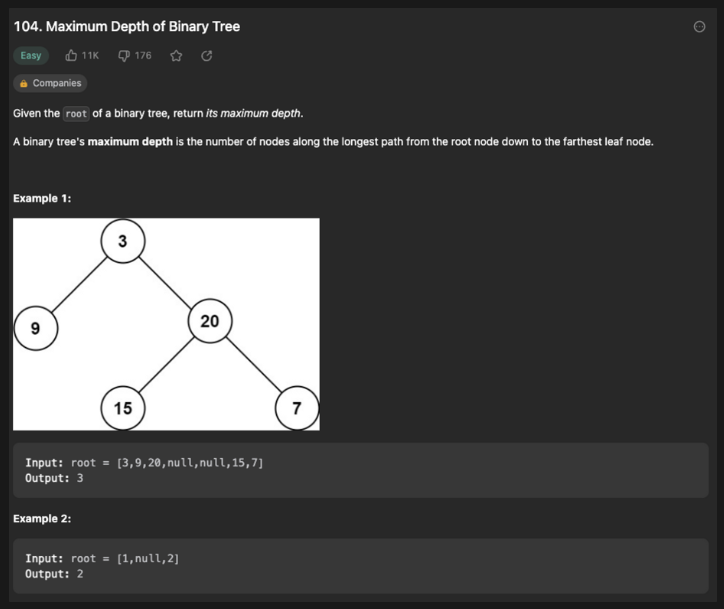
이진트리의 최대 깊이를 구하는 문제로 보인다. 트리의 루트에서 가장 깊은 잎(leaf) 노드까지의 경로를 따라 노드의 수를 계산한다.
# leetcode : Maximum Depth of Binary Tree - 트리
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
# 가장 먼저 입력값이 없으면 (항상 예외 처리를 먼저 신경쓰자)
if root is None:
return 0
else:
left_height = self.maxDepth(root.left)
right_height = self.maxDepth(root.right)
return max(left_height, right_height) + 1class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if root is None:
return 0
queue = collections.deque([root])
depth = 0
while queue:
depth += 1
for _ in range(len(queue)):
current_root = queue.popleft()
if current_root.left:
queue.append(current_root.left)
if current_root.right:
queue.append(current_root.right)
return depthleetcode : Longest Univalue Path
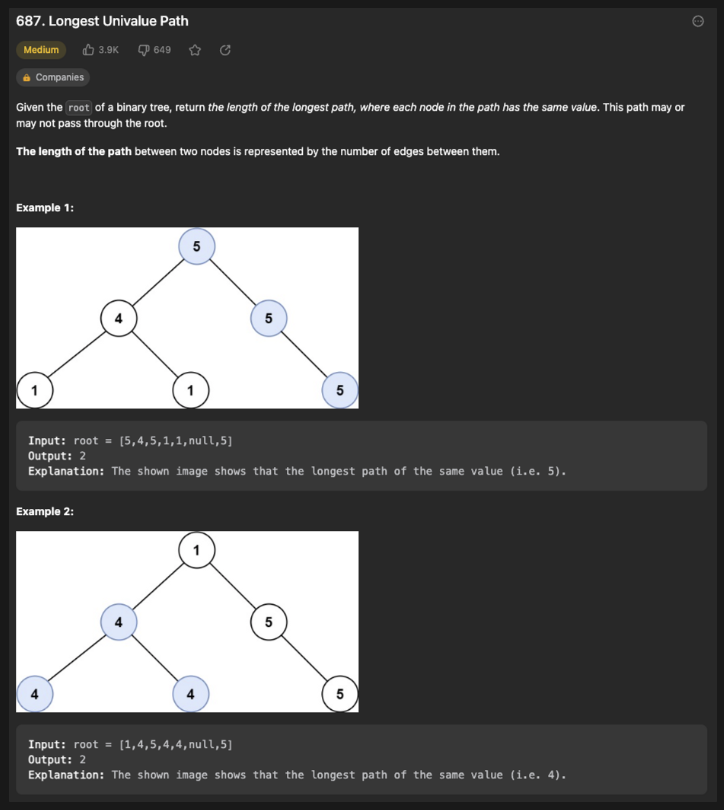
이진 트리에서 같은 값을 가진 노드를 연결하는 가장 긴 경로의 길이를 찾는 문제로 보인다. 각 노드에 대해 재귀적으로 계산하여 왼쪽, 오른쪽 방향으로 같은 값을 가지는 노드의 길이를 반복한다. 같은 값을 가지고 있지 않다면 해당 방향의 길이는 0 으로 만든다.
# leetcode : Longest Univalue Path
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def longestUnivaluePath(self, root: Optional[TreeNode]) -> int:
self.ans = 0
def arrow_length(node):
if not node:
return 0
left_length = arrow_length((node.left))
right_length = arrow_length(node.right)
left_arrow = right_arrow = 0
if node.left and node.left.val == node.val:
left_arrow = left_length + 1
if node.right and node.right.val == node.val:
right_arrow = right_length + 1
self.ans = max(self.ans, left_arrow + right_arrow)
return max(left_arrow, right_arrow)
arrow_length(root)
return self.ansclass Solution:
def longestUnivaluePath(self, root: Optional[TreeNode]) -> int:
self.longest_path = 0
def dfs(node):
if not node:
return 0
left_length = dfs(node.left)
right_length = dfs(node.right)
left_arrow = right_arrow = 0
if node.left and node.left.val == node.val:
left_arrow = left_length + 1
if node.right and node.right.val == node.val:
right_arrow = right_length + 1
self.longest_path = max(self.longest_path, left_arrow + right_arrow)
return max(left_arrow, right_arrow)
dfs(root)
return self.longest_pathleetcode : Balanced Binary Tree
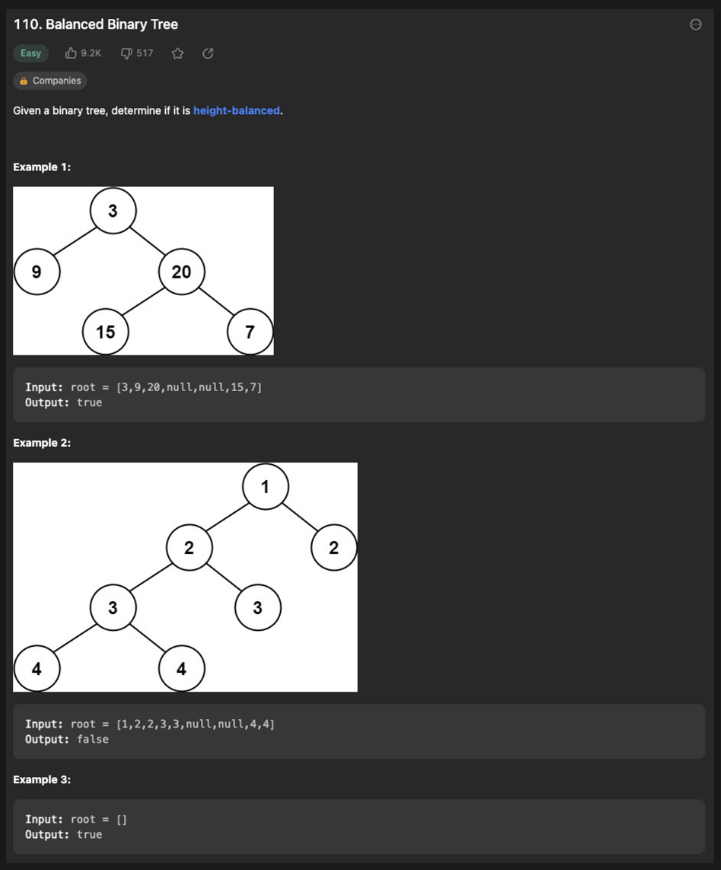
이진트리가 높이 균형(height - balanced)인지 판단하는 문제로 보여진다. 높이 균형트리란 모든 노드의 두 서브트리 같의 높이 차이가 1 이하인 트리를 말한다.
# leetcode : Balanced Binary Tree
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
def check(root):
if root is None:
return 0
left = check(root.left)
right = check(root.right)
if left == -1 or right == -1 or abs(left - right) > 1:
return -1
return max(left, right) + 1
return check(root) != -1class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
def check_height(node):
if not node:
return 0
left_height = check_height(node.left)
right_height = check_height(node.right)
if left_height == -1 or right_height == -1 or abs(left_height - right_height) > 1:
return -1
return max(left_height, right_height) + 1
return check_height(root) != -1leetcode : Minimum Height Trees
그래프에서 루트를 어떤 노드로 설정하느냐에 따라 트리의 높이가 달라지는 점을 이용해 모든 루트 중에서 트리의 높이를 최소로 하는 루트를 찾는 문제로 보인다.
- 그래프를 인접 리스트로 변환한다.
- 단계별로 리프 노드를 제거하며 그래프를 축소한다.
- 리프 노드가 남아있는 마지막 단계의 리프노드가 최소 높이 트리의 루트 노드이다.
# leetcode : Minimum Height Trees
class Solution:
def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:
if n <= 1:
return [0]
graph = collections.defaultdict(list)
for i, j in edges:
graph[i].append(j)
graph[j].append(i)
leaves = []
for i in range(n + 1):
if len(graph[i]) == 1:
leaves.append(i)
while n > 2:
n -= len(leaves)
new_leaves = []
for leaf in leaves:
neighbor = graph[leaf].pop()
graph[neighbor].remove(leaf)
if len(graph[neighbor]) == 1:
new_leaves.append(neighbor)
leaves = new_leaves
return leavesleetcode : Range Sum of BST
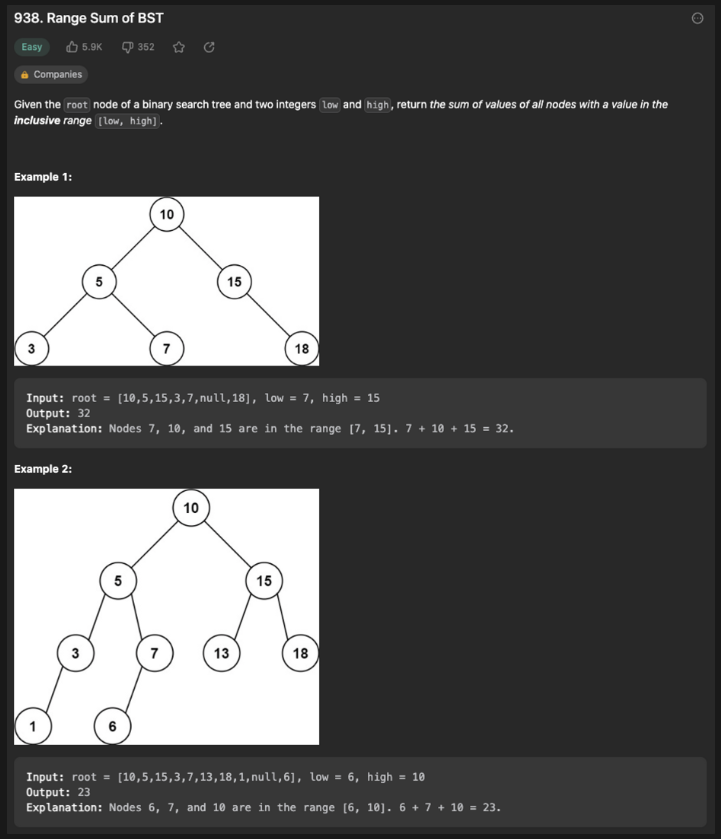
트리와 범위가 주어지고 해당 트리에서 주어진 범위의 노드 값을 모두 더하는 문제로 보인다.
# leetcode : Range Sum of BST
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:
def dfs(node):
if not node:
return 0
if low <= node.val <= high:
self.total += node.val
if low < node.val:
dfs(node.left)
if node.val < high:
dfs(node.right)
self.total = 0
dfs(root)
return self.totalclass Solution:
def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:
self.answer = 0
# node 트리 탐색 하겠다!
def dfs(node):
if not node:
return 0
if low <= node.val <= high:
self.answer += node.val
if low < node.val:
dfs(node.left)
if high > node.val:
dfs(node.right)
dfs(root)
return self.answer