
> 과제 요구사항
유클리드 호제법과 확장 유클리드 호제법을 모두 이용하여 두 수 a,b에 대한 b * t = 1(mod a)를 만족하는 b의 역수 t를 구하여라.
주의사항은 다음과 같다.
- Big num(비트 또는 16진수 문자열 형식)을 이용하여 두 수 a, b를 입력받아야 함.
- q, r0, r1, r, s0, s1, s, t0, t1, t의 값이 변하는 과정이 모두 보여야 함.
- 무작위 값 a, b를 입력할 것이므로 a와 b가 서로소의 관계를 갖지 않을 수도 있음.
> 출력 예시
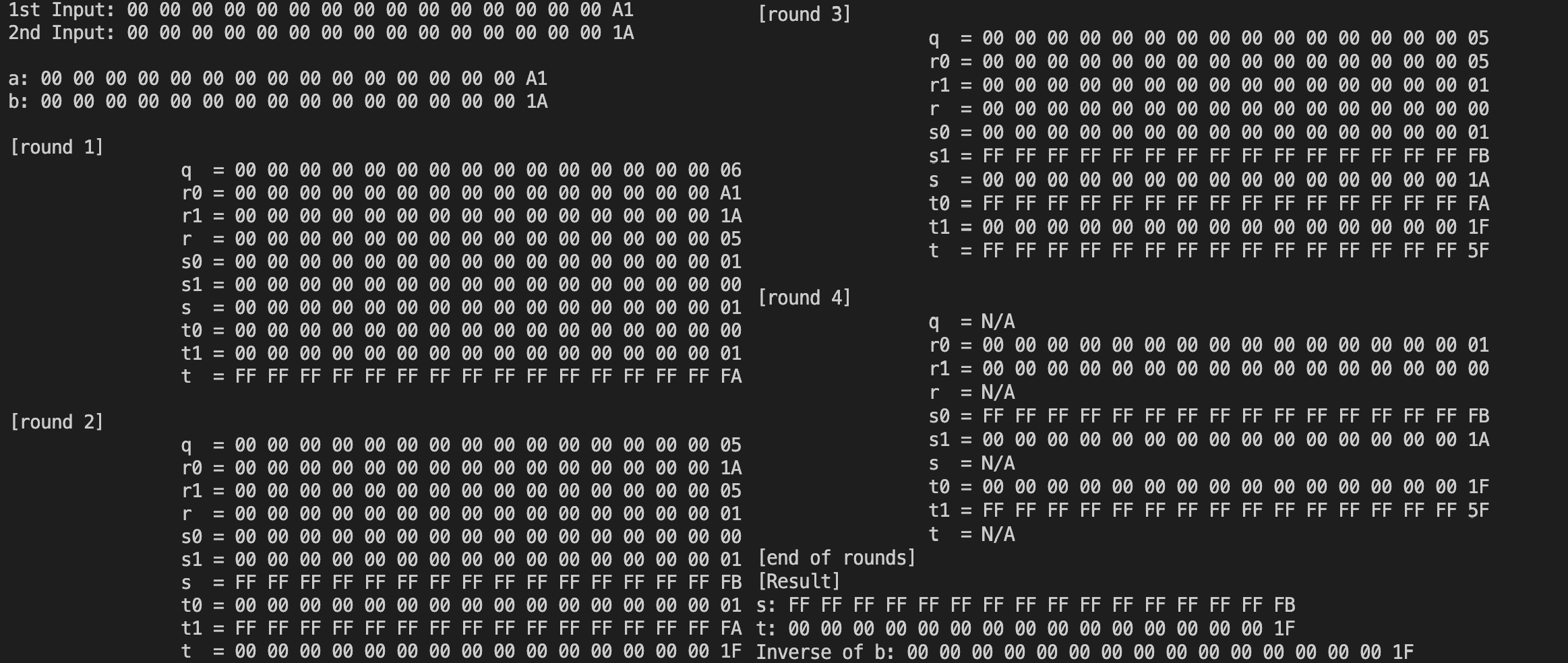
[그림 - 예시 1]

[그림 - 예시 2]
> 코드
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
void CreateBin(char* binArr);
void PrintHex(char* binArr);
void TwoCT(char* binArr, char* _binArr);
void binAdd(char* binArr1, char* binArr2, char* resAdd);
void binSub(char* binArr1, char* binArr2, char* resSub);
void binMul(char* binArr1, char* binArr2, char* resMul);
int power(char* arr);
int Compare(char* binArr1, char* binArr2);
void RightSft(char* arr);
void binDivQuot(char* binArr1, char* binArr2, char* resDivQuot);
void binDivRmd(char* binArr1, char* binArr2, char* resDivRmd);
int coprime(char* binArr1, char* binArr2);
int main(void)
{
char q[128] = { 0 };
char r0[128] = { 0 }, r1[128] = { 0 }, r[128] = { 0 }, _r[128] = { 0 };
char s1[128] = { 0 }, s0[128] = { 0 }, s[128] = { 0 }, _s[128] = { 0 }; s0[127] = 1;
char t0[128] = { 0 }, t1[128] = { 0 }, t[128] = { 0 }, _t[128] = { 0 }; t1[127] = 1;
do
{
printf("1st Input: "); CreateBin(r0);
printf("2nd Input: "); CreateBin(r1);
if (coprime(r0, r1) == 1)
break;
else
printf("입력된 두 수가 서로소가 아닙니다!\n\n 재입력>>\n");
} while (1);
printf("\na: "); PrintHex(r0);
printf("b: "); PrintHex(r1);
for (int i = 1; ; i++)
{
printf("\n[round %d]\n", i);
printf("\t\tq = "); binDivQuot(r0, r1, q); PrintHex(q);
printf("\t\tr0 = "); PrintHex(r0);
printf("\t\tr1 = "); PrintHex(r1);
printf("\t\tr = "); binDivRmd(r0, r1, r); PrintHex(r);
printf("\t\ts0 = "); PrintHex(s0);
printf("\t\ts1 = "); PrintHex(s1);
printf("\t\ts = "); binMul(s1, q, _s); binSub(s0, _s, s); PrintHex(s);
printf("\t\tt0 = "); PrintHex(t0);
printf("\t\tt1 = "); PrintHex(t1);
printf("\t\tt = "); binMul(t1, q, _t); binSub(t0, _t, t); PrintHex(t);
for (int i = 0; i < 128; i++)
{
r0[i] = r1[i]; r1[i] = r[i];
s0[i] = s1[i]; s1[i] = s[i];
t0[i] = t1[i]; t1[i] = t[i];
}
if (power(r) == 0) {
printf("\n[round %d]\n", i + 1);
printf("\t\tq = N/A\n");
printf("\t\tr0 = "); PrintHex(r0);
printf("\t\tr1 = "); PrintHex(r1);
printf("\t\tr = N/A\n");
printf("\t\ts0 = "); PrintHex(s0);
printf("\t\ts1 = "); PrintHex(s1);
printf("\t\ts = N/A\n");
printf("\t\tt0 = "); PrintHex(t0);
printf("\t\tt1 = "); PrintHex(t1);
printf("\t\tt = N/A\n");
printf("[end of rounds]\n[Result]\n");
printf("s: "); PrintHex(s0);
printf("t: "); PrintHex(t0);
printf("Inverse of b: "); PrintHex(t0);
break;
}
}
return 0;
}
void CreateBin(char* binArr) {
int a = 0;
for (int i = 1; i <= 16; i++) { //16진수 두자리씩 입력을 총 16번 반복 (8bit * 16 = 128bit)
scanf("%x", &a); //16진수 두자리씩 입력
for (int j = 0; j < 8; j++) { // 입력받은 두자리 16진수를 2진수로 변환
binArr[i * 8 - j - 1] = a % 2; // mod 2 연산을 통해 8자리 2진수를 배열 8칸에서 뒤에서부터 저장
a /= 2;
}
a = 0;
}
} //char형 128크기의 배열을 전달받아 입력 받은 16진수를 2진수로 저장하는 함수
void PrintHex(char* binArr) {
int p = 1, res = 0;
for (int i = 1; i <= 16; i++) { //2진수 8자리씩 공백을 두고 16진수로 출력
for (int j = 0; j < 8; j++) {
res += binArr[i * 8 - 1 - j] * p; //2진수 8자리 중 n번째자리에 2^(n-1)곱하고 그 값을 res에 더하기(첫번째 자리부터 시작)
p *= 2; // n번째 자리에 2^(n-1)을 곱하기 위해 p에 2 곱하여 저장
}
printf("%02X ", res);
res = 0, p = 1; //2진수 다음 8자리 출력을 위해 res, p를 0과 1로 다시 초기화
}
printf("\n");
} //char형 배열에 2진수로 저장된 수를 16진수로 출력하는 함수
void TwoCT(char* binArr, char* _binArr) {
for (int i = 0; i < 128; i++) {
if (binArr[i] == 1)
_binArr[i] = 0;
else
_binArr[i] = 1;
} // 2의 보수를 취하기 위해 1을 0으로, 0을 1로 변환
for (int i = 127; i >= 0; i--) { // 2의 보수를 취하기 위해 마지막에 +1을 진행
if (_binArr[i] == 1)
_binArr[i] = 0; //배열의 끝에서부터, 저장된 값이 1이라면 올림값이 생기고 0으로 변환
else {
_binArr[i] = 1;
break; //배열의 끝에서부터, 처음으로 저장된 값이 0이라면 올림값 1을 더하고 반복문을 빠져나옴
}
}
} //배열을 전달받아 2의 보수를 취하는 함수
void binAdd(char* binArr1, char* binArr2, char* resAdd)
{
char carry = 0; // 2진수의 덧셈 연산에서 올림을 위해 변수 carry 선언
for (int i = 127; i >= 0; i--) {
int tempRes = (binArr1[i]) + (binArr2[i]) + carry; // 두 2진수의 각 자리를 더하고 이전 자리에서 올림 수 더하기
if (tempRes < 2) { // 0 or 1
carry = 0; // 2진수의 덧셈 연산에서 올림을 안한다면 carry에 0 저장
}
else { // 2 or 3
carry = 1;// 2진수의 덧셈 연산에서 올림을 안한다면 carry에 1 저장
}
resAdd[i] = tempRes % 2; // 두 2진수의 각 자리를 더한 값에 의해 올림을 마친 후 값 저장을 위해 mod 2 연산 취하기
}
} // 두 2진수를 전달 받아 덧셈 연산을 행하고 결과를 resAdd에 저장하는 함수
void binSub(char* binArr1, char* binArr2, char* resSub) {
char _binArr2[128] = { 0 };
TwoCT(binArr2, _binArr2);//뺄셈 연산을 진행하기 위해 두 번째 전달인자를 2의 보수를 취해 동일 절댓값의 음수로 변환
char carry = 0; // 2진수의 덧셈 연산에서 올림을 위해 변수 carry 선언
for (int i = 127; i >= 0; i--) {
int tempRes = (binArr1[i]) + (_binArr2[i]) + carry; // 두 2진수의 각 자리를 더하고 이전 자리에서 올림 수 더하기
if (tempRes < 2) { // 0 or 1
carry = 0; // 2진수의 덧셈 연산에서 올림을 안한다면 carry에 0 저장
}
else { // 2 or 3
carry = 1;// 2진수의 덧셈 연산에서 올림을 안한다면 carry에 1 저장
}
resSub[i] = tempRes % 2; // 두 2진수의 각 자리를 더한 값에 의해 올림을 마친 후 값 저장을 위해 mod 2 연산 취하기
}
}//두 2진수를 전달 받아 뺄셈 연산(전달인자1 - 전달인자2)을 행하고 결과를 resSub에 저장하는 함수
void binMul(char* binArr1, char* binArr2, char* resMul) {
char savRes[128] = { 0 };
for (int i = 127; i >= 0; i--) {
char tempRes[128] = { 0 }; //binArr1에 binArr2의 각 자릿수를 곱한 값을 저장하는 변수 tempRes 선언
int cnt = 127 - i; // 2진수의 shift 연산을 위한 변수 cnt 선언
if (binArr2[i] == 0)
continue; //binArr2의 각 자릿수에서 0은 곱한 결과값이 0이므로 무시하고 다음 단계 실행
else
for (int j = 127; j >= 0; j--) {
if (j - cnt < 0) //tempRes에 저장할 때 128bit를 넘어가는 것은 무시
break;
else
tempRes[j - cnt] = binArr1[j]; // binArr1의 값을 2진수의 left shift 연산을 취하여 tempRes에 저장
}
binAdd(savRes, tempRes, savRes); //binArr1에 binArr2의 각 자릿수를 곱할 때마다 이전까지의 결과값에 bArrAddforMUl 함수를 통해 더해줌
}
for (int i = 127; i >= 0; i--)
resMul[i] = savRes[i]; //binArr1에 binArr2의 모든 자릿수를 곱한 후 저장된 결과값을 resMul로 복사
}// 두 2진수를 전달 받아 곱셈 연산을 행하고 결과를 resMul에 저장하는 함수
int power(char* arr)
{
int k = 0;
for (int i = 0; i < 128; i++)
{
if (arr[i] == 0)
continue;
else {
k = 128 - i; break;
} // arr의 0번째 공간(큰 자릿수)부터 확인하여 처음으로 1이 나온 자리를 k로 지정
}
return k;
}// arr에 저장된 2진수가 2^k의 자리 수인 것을 확인하고 k를 반환하는 함수
int Compare(char* binArr1, char* binArr2)
{
if (power(binArr1) == power(binArr2)) {
for (int i = 0; i < 128; i++) {
if (binArr1[i] ^ binArr2[i]) { // 두 2진수 배열의 같은 자릿수의 수가 다른 경우
if (binArr1[i] == 0)
return 2; //binArr1의 값이 0이면 binArr2>binArr1이고, 2를 반환
else
return 1; //binArr2의 값이 0이면 binArr1>binArr2이고, 1을 반환
}
else {
if (i == 127)
return 3; // 처음부터 끝까지 모두 같은 경우 binArr1=binArr2이므로 3을 반환
else
continue; //2진수의 첫째짜리까지 도달하지 않았으므로 작은 자릿수를 다시 비교
}
}
}
else if (power(binArr1) > power(binArr2))
return 1; //binArr1의 자릿수가 binArr2의 자릿수보다 크기에 binArr1>binArr2이고, 1을 반환
else
return 2; //binArr2의 자릿수가 binArr1의 자릿수보다 크기에 binArr2>binArr1이고, 2를 반환
} // 두 2진수 배열 binArr1과 binArr2를 전달받아, binArr1>binArr2이면 1을, binArr2>binArr1이면 2를, binArr1=binArr2이면 3을 반환하는 함수
void RightSft(char* arr)
{
for (int i = 127; i >= 0; i--) {
if (i == 0)
arr[i] = 0;
else
arr[i] = arr[i - 1];
}
}// arr에 저장된 2진수를 Right shift 시키는 함수 (2로 나누는 것과 동일)
void binDivQuot(char* binArr1, char* binArr2, char* resDivQuot)
{
int dif = 0, q = 0;
char* LSarr2 = (char*)calloc(128, sizeof(char));
char* quot = (char*)calloc(128, sizeof(char));
char* div = (char*)calloc(128, sizeof(char));
//전달 받은 2진수를 복사하고 몫을 저장하기 위해 메모리 공간 동적할당
if (power(binArr1) > power(binArr2))
dif = power(binArr1) - power(binArr2);
else
dif = power(binArr2) - power(binArr1);//left shift를 위해 두 2진수의 최대자릿수(n)의 차이를 구해서 dif에 저장
for (int i = 127; i >= 0; i--) {
if (i - dif < 0) //LSarr2에 저장할 때 128bit를 넘어가는 것은 무시
break;
else
LSarr2[i - dif] = binArr2[i]; // binArr2의 값을 2진수의 left shift 연산을 취하여 LSarr2에 저장
}
for (int i = 0; i < 128; i++) {
div[i] = binArr1[i];
} // 나눗셈 연산을 진행하기 위해 나눠지는 수 binArr1을 div에 복사
for (q = dif; q >= 0; q--) {
if (Compare(div, LSarr2) == 1) { //나눠지는 수가 나누는 수의 left shift 결과보다 큰 경우
binSub(div, LSarr2, div); //나눠지는 수에서 나누는 수의 left shift 결과를 빼고, 다음 연산을 위해 결과를 다시 나눠지는 수에 저장
RightSft(LSarr2); // 다음 연산을 위해 나누는 수의 left shift 결과를 1만큼 right shift
quot[127 - q] = 1; //나누는 수의 left shift한 자리에서 뺄셈이 이루어졌으므로 몫을 나타내는 2진수의 자리에 1 저장
continue;
}
if (Compare(div, LSarr2) == 2) { //나누는 수의 left shift 결과가 나눠지는 수보다 큰 경우
RightSft(LSarr2); // 다음 연산을 위해 나누는 수의 left shift 결과를 1만큼 right shift
continue;
}
if (Compare(div, LSarr2) == 3) { //나눠지는 수와 나누는 수의 left shift 결과가 같은 경우
quot[127 - q] = 1; //나누는 수의 left shift한 자리에서 뺄셈이 이루어졌으므로 몫을 나타내는 2진수의 자리에 1 저장
break; //나누어 떨어졌으므로 나눗셈 과정 끝
}
}
for (int i = 0; i < 128; i++)
resDivQuot[i] = quot[i]; //나눗셈 과정을 진행한 결과인 몫 quot를 resDivQuot에 복사
free(LSarr2), free(quot), free(div); //동적 할당 해제
}// 두 2진수를 전달 받아 나눗셈 연산을 행하고 몫을 resDivQuot에 저장하는 함수
void binDivRmd(char* binArr1, char* binArr2, char* resDivRmd)
{
char _quot[128] = { 0 }, tempres[128] = { 0 };
binDivQuot(binArr1, binArr2, _quot); //두 2진수를 나눈 몫을 _quot에 저장
binMul(binArr2, _quot, tempres); //몫인 _quot와 나누었던 2진수 binArr2를 곱하여 tempres에 저장
binSub(binArr1, tempres, resDivRmd); //나눠지는 2진수 binArr1에서 tempres를 빼서 나눗셈의 나머지를 resDivRmd에 저장
}// 두 2진수를 전달 받아 나눗셈을 진행하고 나머지를 resDivRmd에 저장하는 함수
int coprime(char* binArr1, char* binArr2)
{
char* arr1 = (char*)calloc(128, sizeof(char));
char* arr2 = (char*)calloc(128, sizeof(char));
char* rmd = (char*)calloc(128, sizeof(char));
//전달 받은 2진수를 복사하고 나눗셈 연산을 진행하기 위해 메모리 공간 동적할당
for (int i = 0; i < 128; i++) {
arr1[i] = binArr1[i];
arr2[i] = binArr2[i]; //arr1에 첫 인자인 2진수를 , arr2에 두번째 인자인 2진수를 복사
}
do
{
binDivRmd(arr1, arr2, rmd); //나눗셈 연산을 수행하고 나머지를 rmd에 저장
if (power(rmd) == 0)
break;
else {
for (int i = 0; i < 128; i++)
{
arr1[i] = arr2[i]; arr2[i] = rmd[i];
}
}
} while (1);// 나머지가 0이 될 때까지 나눗셈 반복
if (power(arr2) == 1)
return 1;
else
return 0; //유클리드 알고리즘에 의해 구한 두 2진수의 gcd가 1이면(서로소라면) 1을 반환, gcd가 1이 아니라면 0을 반환
free(arr1), free(arr2), free(rmd); //동적할당 해제
}