
> 과제 요구사항
주어진 데이터에서 주택 가격(실제로 단위 면적당 주택 가격)과 기타 관련 변수 간의 관계를 파악하려고 한다. 우리는 다양한 회귀 기술을 사용할 것입니다.회귀분석은 다른 변수(독립 변수)를 기반으로 한 변수(종속 변수)의 값을 예측하는 데 사용되는 기술이다. 데이터 세트를 기반으로 특정 가정을 하기 때문에 본질적으로 매개변수적이다. 데이터 세트가 이러한 가정을 따르는 경우 회귀는 좋은 성능을 제공한다. 그렇지 않으면 설득력 있는 정확성을 제공하는 데 어려움을 겪을 수 있다.
회귀는 기본적으로 주어진 교육 데이터를 기반으로 모델을 교육하고 모델이 종속 변수와 독립 변수 사이의 관련성을 시도한다는 것을 의미하는 지도 학습의 일부이다. 독립 변수를 종속 변수에 매핑하는 다양한 기능을 사용하여 이를 수행한다. 모델이 완전히 훈련되고 오류가 최소화되면 테스트 데이터에서도 예측을 할 수 있다.
> 단순 선형 회귀(Simple Linear Regression)
기본적이고 일반적으로 사용되는 유형의 예측 분석입니다. 이러한 회귀 추정치는 다음을 설명하는 데 사용됩니다.
하나의 종속 변수와 하나 이상의 독립 변수 사이의 관계. y = aX + b에서
- y – 종속 변수
- X – 독립 변수
- b – 절편
- a – 기울기
> 다중 선형 회귀(Multiple Linear Regression)
이 또한 기본적이고 일반적으로 사용되는 예측 분석 유형입니다. 이러한 회귀 추정치는 다음을 설명하는 데 사용됩니다.
하나의 종속 변수와 하나 이상의 독립 변수 사이의 관계. y = b+a1X1 +a2X2 +
a3X3 + a4X4 + . . . 에서
- y – 종속 변수
- X1, X2, X3, X4 – 독립 변수
- b – 절편
- a1, a2, a3, · · · – 기울기
> 다항식 회귀(Polynomial Regression)
기본적이고 일반적으로 사용되는 유형의 예측 분석입니다. 이러한 회귀 추정치는 하나의 종속 변수와 하나의 독립 변수 사이의 관계를 설명하는 데 사용됩니다. y = a0 + a1X + a2X2 + a3X3 + a4X4 + . . . 에서
- y – 종속 변수
- X – 독립 변수
- a0, a1, a2, a3, a4, · · · - 계수
우리의 과제에서는 네가지 전략을 사용하게 된다.
- 단순 선형 회귀(SLR) : X1, X2, · · ·, X6을 시도하고 최상의 변수를 선택합니다. 64개의 테스트 데이터에 대해 최상의 평균 제곱 오차(MSE)를 제공합니다.
- 다중 선형 회귀(MLR) : X1, X2, · · ·, X6을 모두 고려할 필요는 없습니다.
- 다항 회귀(PR) : X1, X2, · · ·, X6을 시도하고 순서에 따라 가장 좋은 변수를 선택합니다. 최대 차수는 6이므로 결정해야 할 매개변수는 7개입니다.
- 혼합 회귀(Combined): 모든 조합을 시도하되 매개변수를 7 이하로 제한해야 합니다.
이러한 전략들로, 주어진 데이터에서 앞부분 350개로 직선을 그리고 뒷부분 64개의 데이터에 대해 회귀분석을 진행한다. 그리고 평균 제곱 오차(MSE)까지 도출해낸다.
> 출력 예시
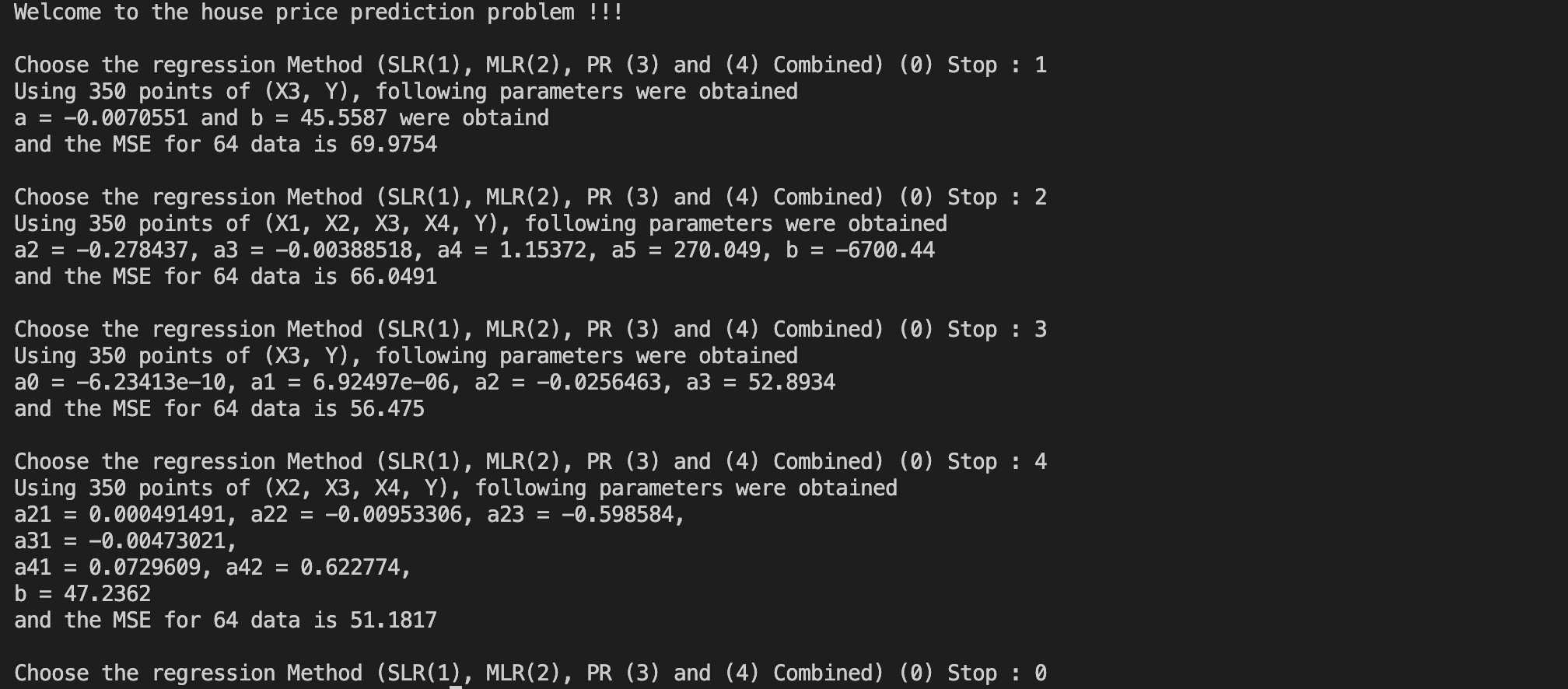
> 코드
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
#include <stdio.h>
using namespace std;
double determin(vector<vector<double> > m) {
if (m.size() == 1)
return m[0][0];
else if (m.size() == 2)
return m[0][0] * m[1][1] - m[0][1] * m[1][0];
else {
int size = m.size();
double dtrm = 0.0;
for (int col = 0; col < size; col++) {
vector<vector<double> > tmp2;
for (int i = 1; i < size; i++) {
vector<double> line;
for (int j = 0; j < size; j++) {
if (j == col)
continue;
double tmp = m[i][j];
line.push_back(tmp);
}
tmp2.push_back(line);
}
if (col % 2 == 0)
dtrm += m[0][col] * determin(tmp2);
else if (col % 2 == 1)
dtrm += m[0][col] * determin(tmp2) * -1;
}
return dtrm;
}
}
class Matrix {
private:
//vector<vector<double>> matrix;
public:
vector<vector<double> > matrix;
Matrix(int row, int col) {
vector<double> v(col, 0);
for (int i = 0; i < row; i++) {
matrix.push_back(v);
}
}
int row_size() {
return matrix.size();
}
int col_size() {
return matrix[0].size();
}
void init_by_col(vector<double> data, int c) {
for (int row = 0; row < matrix.size(); row++) {
matrix[row][c - 1] = data[row]; //2열의 index는 1이니까
}
}
void init_by_row(vector<double> data, int r) {
for (int col = 0; col < matrix[0].size(); col++) {
matrix[r - 1][col] = data[col];
}
}
void transpose(Matrix m1) {
for (int col = 0; col < m1.matrix[0].size(); col++) {
for (int row = 0; row < m1.matrix.size(); row++) {
matrix[col][row] = m1.matrix[row][col];
}
}
}
Matrix mul(Matrix m1) {
Matrix ans(matrix.size(), m1.matrix[0].size());
for (int i = 0; i < matrix.size(); i++) {
vector<double> row;
for (int j = 0; j < m1.matrix[0].size(); j++) {
double tmp = 0;
for (int n = 0; n < matrix[i].size(); n++) {
tmp += matrix[i][n] * m1.matrix[n][j];
}
row.push_back(tmp);
}
ans.init_by_row(row, i + 1);
}
return ans;
}
double determinant() {
return determin(matrix);
}
Matrix cofactor() {
int size = matrix.size();
vector<vector<double> > cfct;
for (int row = 0; row < size; row++) {
vector<double> co_line;
for (int col = 0; col < size; col++) {
double tmp2 = 0;
vector<vector<double> > tmp_all;
for (int i = 0; i < size; i++) {
vector<double> tmp_line;
if (i == row)
continue;
for (int j = 0; j < size; j++) {
if (j == col)
continue;
double tmp = matrix[i][j];
tmp_line.push_back(tmp);
}
tmp_all.push_back(tmp_line);
}
if ((col + row) % 2 == 0)
tmp2 = determin(tmp_all);
else if ((col + row) % 2 == 1)
tmp2 = determin(tmp_all) * -1;
co_line.push_back(tmp2);
}
cfct.push_back(co_line);
}
Matrix ans(cfct.size(), cfct[0].size());
for (int row = 0; row < cfct.size(); row++) {
for (int col = 0; col < cfct[0].size(); col++)
ans.matrix[row][col] = cfct[row][col];
}
return ans;
}
Matrix divide(double dtrm) {
Matrix ans(matrix.size(), matrix[0].size());
if (dtrm == 0) {
cout << "matrix's determinant is zero!\n" << endl;
for (int row = 0; row < matrix.size(); row++) {
for (int col = 0; col < matrix[0].size(); col++) {
ans.matrix[row][col] = matrix[row][col];
}
}
return ans;
}
for (int row = 0; row < matrix.size(); row++) {
for (int col = 0; col < matrix[0].size(); col++) {
ans.matrix[row][col] = matrix[row][col] / dtrm;
}
}
return ans;
}
Matrix inverse() {
Matrix ans(matrix.size(), matrix[0].size());
for (int row = 0; row < matrix.size(); row++) {
for (int col = 0; col < matrix[0].size(); col++) {
ans.matrix[row][col] = matrix[row][col];
}
}
double dtrm = ans.determinant();
ans = ans.cofactor();
ans.transpose(ans);
ans = ans.divide(dtrm);
return ans;
}
void print() {
for (int row = 0; row < matrix.size(); row++) {
for (int col = 0; col < matrix[0].size(); col++) {
cout << matrix[row][col] << " ";
}
putchar('\n');
}
}
};
int main()
{
FILE* fp = fopen("Real_Estate_Data.txt", "r");
char tmp[100] = { 0, };
int num;
double one, two, three, four, five, six, seven;
vector<double> v1, v2, v3, v4, v5, v6, y, idt;
vector<double> sv1, sv2, sv3, sv4; //
vector<double> tv1, tv2, tv3, tv4; //
vector<double> rx1, rx2, rx3, rx4, rx5, rx6, ry;
vector<double> rsx1, rsx2, rsx3, rsx4; //
vector<double> rtx1, rtx2, rtx3, rtx4; //
if (fp == NULL)
{
cout << "Failed to open file!\n" << endl;
return 0;
}
for (int i = 0; i < 350; i++) {
fscanf(fp, "%d\t%lf\t%lf\t%lf\t%lf\t%lf\t%lf\t%lf", &num, &one, &two, &three, &four, &five, &six, &seven);
v2.push_back(two); sv2.push_back(two * two); tv2.push_back(two * two * two);
v3.push_back(three); sv3.push_back(three * three); tv3.push_back(three * three * three);
v4.push_back(four); sv4.push_back(four * four); tv4.push_back(four * four * four);
v5.push_back(five);
v6.push_back(six);
y.push_back(seven);
idt.push_back(1);
}
for (int i = 0; i < 64; i++) {
fscanf(fp, "%d\t%lf\t%lf\t%lf\t%lf\t%lf\t%lf\t%lf", &num, &one, &two, &three, &four, &five, &six, &seven);
rx1.push_back(one); rsx1.push_back(one * one); rtx1.push_back(one * one * one);
rx2.push_back(two); rsx2.push_back(two * two); rtx2.push_back(two * two * two);
rx3.push_back(three); rsx3.push_back(three * three); rtx3.push_back(three * three * three);
rx4.push_back(four); rsx4.push_back(four * four); rtx4.push_back(four * four * four);
rx5.push_back(five);
rx6.push_back(six);
ry.push_back(seven);
}
int flag = 0;
cout << "Welcome to the house price prediction problem !!!" << endl;
while (1) {
if (flag == 1) {
break;
}
else {
int option;
cout << "\nChoose the regression Method (SLR(1), MLR(2), PR (3) and (4) Combined) (0) Stop : ";
cin >> option;
switch (option) {
case 0: {
flag = 1;
break;
}
case 1: {
Matrix ex(350, 2);
ex.init_by_col(v3, 1);
ex.init_by_col(idt, 2); //M
Matrix Y(350, 1);
Y.init_by_col(y, 1); //W
Matrix t_ex(2, 350);
t_ex.transpose(ex);
Matrix tmp_m1 = t_ex.mul(ex); //t_M * M
Matrix inverse = tmp_m1.inverse();
Matrix tmp_m2 = t_ex.mul(Y); // t_M * W
Matrix sol = inverse.mul(tmp_m2);
double A = sol.matrix[0][0];
double B = sol.matrix[1][0];
Matrix sample(64, 2);
double MSE = 0;
sample.init_by_col(rx3, 1);
sample.init_by_col(idt, 2);
Matrix smp_y = sample.mul(sol);
for (int i = 0; i < 64; i++) {
double diff = smp_y.matrix[i][0] - ry[i];
MSE += diff * diff;
}
MSE /= 64;
cout << "Using 350 points of (X3, Y), following parameters were obtained" << endl;
cout << "a = " << A << " and b = " << B << " were obtaind" << endl;
cout << "and the MSE for 64 data is " << MSE << endl;
break;
}
case 2: {
Matrix ex(350, 5);
ex.init_by_col(v2, 1); ex.init_by_col(v3, 2); ex.init_by_col(v4, 3); ex.init_by_col(v5, 4); ex.init_by_col(idt, 5);
Matrix Y(350, 1);
Y.init_by_col(y, 1);
Matrix t_ex(5, 350);
t_ex.transpose(ex);
Matrix tmp_m1 = t_ex.mul(ex);
Matrix inverse = tmp_m1.inverse();
Matrix tmp_m2 = t_ex.mul(Y);
Matrix sol = inverse.mul(tmp_m2);
double A1 = sol.matrix[0][0];
double A2 = sol.matrix[1][0];
double A3 = sol.matrix[2][0];
double A4 = sol.matrix[3][0];
double B = sol.matrix[4][0];
Matrix sample(64, 5);
double MSE = 0;
sample.init_by_col(rx2, 1); sample.init_by_col(rx3, 2); sample.init_by_col(rx4, 3); sample.init_by_col(rx5, 4); sample.init_by_col(idt, 5);
Matrix smp_y = sample.mul(sol);
for (int i = 0; i < 64; i++) {
double diff = smp_y.matrix[i][0] - ry[i];
MSE += diff * diff;
}
MSE /= 64;
cout << "Using 350 points of (X1, X2, X3, X4, Y), following parameters were obtained" << endl;
cout << "a2 = " << A1 << ", a3 = " << A2 << ", a4 = " << A3 << ", a5 = " << A4 << ", b = " << B << endl;
cout << "and the MSE for 64 data is " << MSE << endl;
break;
}
case 3: {
Matrix ex(350, 4);
ex.init_by_col(tv3, 1); ex.init_by_col(sv3, 2); ex.init_by_col(v3, 3); ex.init_by_col(idt, 4);
Matrix Y(350, 1);
Y.init_by_col(y, 1);
Matrix t_ex(4, 350);
t_ex.transpose(ex);
Matrix tmp_m1 = t_ex.mul(ex);
Matrix inverse = tmp_m1.inverse();
Matrix tmp_m2 = t_ex.mul(Y);
Matrix sol = inverse.mul(tmp_m2);
double A0 = sol.matrix[0][0];
double A1 = sol.matrix[1][0];
double A2 = sol.matrix[2][0];
double B = sol.matrix[3][0];
Matrix sample(64, 4);
double MSE = 0;
sample.init_by_col(rtx3, 1); sample.init_by_col(rsx3, 2); sample.init_by_col(rx3, 3); sample.init_by_col(idt, 4);
Matrix smp_y = sample.mul(sol);
for (int i = 0; i < 64; i++) {
double diff = smp_y.matrix[i][0] - ry[i];
MSE += diff * diff;
}
MSE /= 64;
cout << "Using 350 points of (X3, Y), following parameters were obtained" << endl;
cout << "a0 = " << A0 << ", a1 = " << A1 << ", a2 = " << A2 << ", a3 = " << B << endl;
cout << "and the MSE for 64 data is " << MSE << endl;
break;
}
case 4:{
Matrix ex(350,7);
ex.init_by_col(tv2,1); ex.init_by_col(sv2,2); ex.init_by_col(v2,3);
ex.init_by_col(v3,4);
ex.init_by_col(sv4,5); ex.init_by_col(v4,6);
ex.init_by_col(idt,7);
Matrix Y(350,1);
Y.init_by_col(y, 1);
Matrix t_ex(7, 350);
t_ex.transpose(ex);
Matrix tmp_m1 = t_ex.mul(ex);
Matrix inverse = tmp_m1.inverse();
Matrix tmp_m2 = t_ex.mul(Y);
Matrix sol = inverse.mul(tmp_m2);
double A21=sol.matrix[0][0]; double A22=sol.matrix[1][0]; double A23=sol.matrix[2][0];
double A31=sol.matrix[3][0];
double A41=sol.matrix[4][0]; double A42=sol.matrix[5][0];
double B=sol.matrix[6][0];
Matrix sample(64,7);
double MSE=0;
sample.init_by_col(rtx2,1); sample.init_by_col(rsx2,2); sample.init_by_col(rx2,3);
sample.init_by_col(rx3,4);
sample.init_by_col(rsx4,5); sample.init_by_col(rx4,6);
sample.init_by_col(idt,7);
Matrix smp_y = sample.mul(sol);
for (int i = 0; i < 64; i++) {
double diff = smp_y.matrix[i][0] - ry[i];
MSE += diff * diff;
}
MSE /= 64;
cout << "Using 350 points of (X2, X3, X4, Y), following parameters were obtained" << endl;
cout << "a21 = " << A21 << ", a22 = " << A22 << ", a23 = " << A23 << "," << endl;
cout << "a31 = " << A31 << "," << endl;
cout << "a41 = " << A41 << ", a42 = " << A42 << "," << endl;
cout << "b = "<< B << endl;
cout << "and the MSE for 64 data is " << MSE << endl;
}
}
}
}
fclose(fp);
return 0;
}> 추가 첨부파일
코드에서 쓰인 Real_Estate_Data.txt이다.
https://drive.google.com/file/d/1bJQOR7RaTgx9dzkmz6ptN7EYFc_B6WPA/view?usp=share_link
주택 가격 데이터의 모음으로, 학습을 위한 데이터가 앞부분 350개, 실험을 위한 데이터가 뒷부분 64개로 구성되어있다.
