[ Python] 행렬곱, 역행렬

> 과제 요구사항

주어진 행렬의 역행렬을 구하고, 구한 역행렬과 원래의 형렬을 곱하여 항등 행렬을 만드는 코드를 짠다.

> 출력 예시

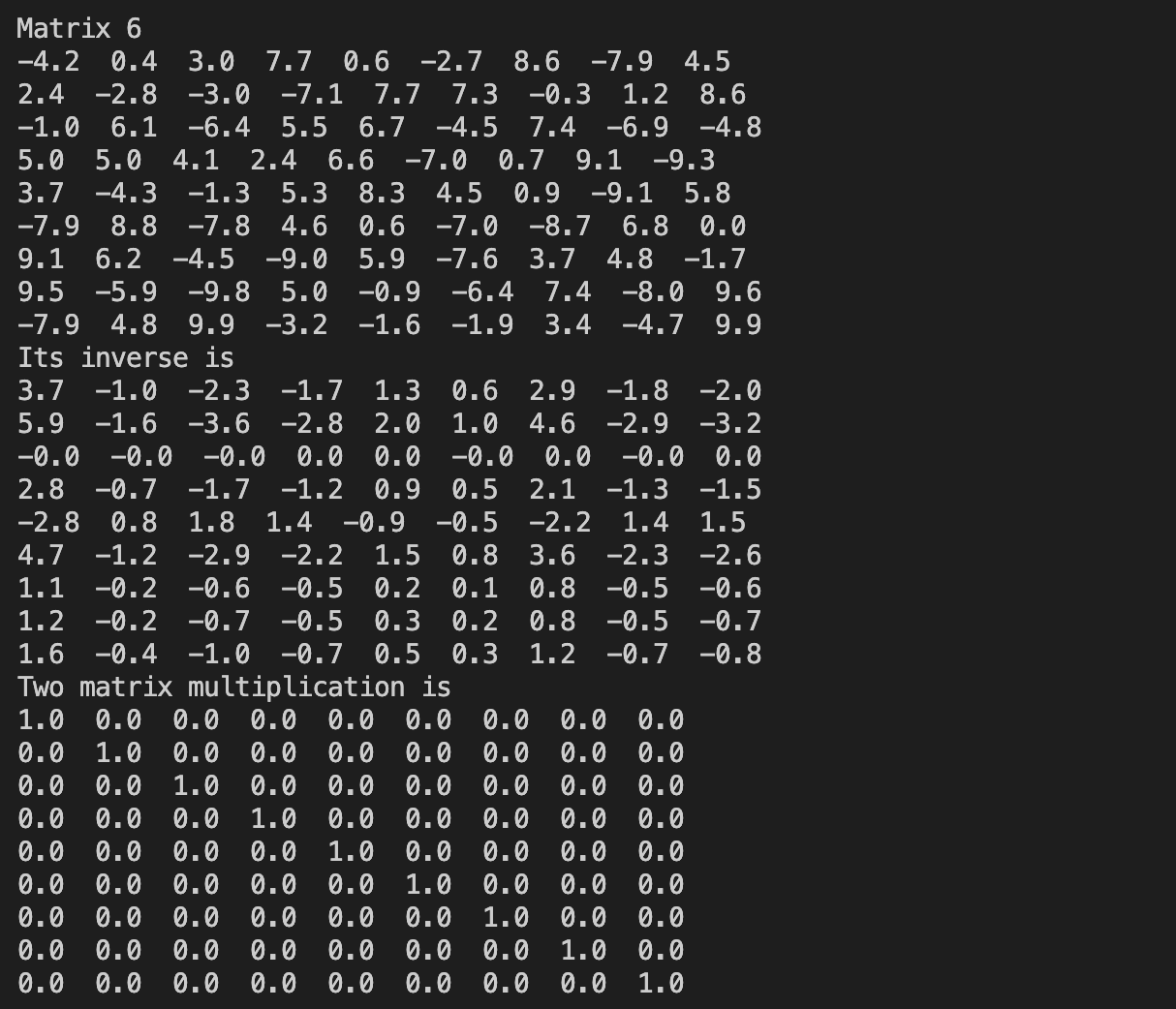
> 코드

def get_matrix_list(document): 
    f=open(document,"r")
    result=[]
    while True:
        line=f.readline()
        if line == '\n':
            continue

        line=line.split()
        f_line=[]
        for i in line:
            f_line.append(float(i))
        size=len(line)

        if size==0:
            break

        matrix=[f_line]
        for i in range(size-1):
            line2=f.readline().split()
            f2_line=[]
            for i in line2:
                f2_line.append(float(i))
            matrix.append(f2_line)
        result.append(matrix)
    return result

def determin(matrix):
    if (len(matrix)==1):
        return matrix[0][0]
    elif (len(matrix)==2):
        return matrix[0][0]*matrix[1][1]-matrix[0][1]*matrix[1][0]
    else:
        size=len(matrix)
        col=0
        dtrm=0.0
        while(col<size):
            tmp2=[]
            for i in range(1,size):
                line=[]
                for j in range(0,size):
                    if j==col:
                        continue
                    tmp=matrix[i][j]
                    line.append(tmp)
                tmp2.append(line)
            if col%2==0:
                dtrm+=matrix[0][col]*determin(tmp2)
            elif col%2==1:
                dtrm+=matrix[0][col]*determin(tmp2)*-1
            col=col+1
        dtrm=round(dtrm,6)
        return dtrm


class Matrix:
    def __init__(self,matrix):
        self.matrix=matrix

    def determinant(self):
        return determin(self.matrix)

    def cofactor_matrix(self):
        size=len(self.matrix)
        cofactor=[]
        row,col=0,0
        while(row<size):
            co_line=[]
            while(col<size):
                tmp2=0
                tmp_all=[]
                for i in range(0,size): #row
                    tmp_line=[]
                    if i==row:
                        continue
                    for j in range(0,size): #col
                        if j==col:
                            continue
                        tmp=self.matrix[i][j]
                        tmp_line.append(tmp)
                    tmp_all.append(tmp_line)
                if (col+row)%2==0:
                    tmp2=determin(tmp_all)
                elif (col+row)%2==1:
                    tmp2=determin(tmp_all)*-1
                co_line.append(tmp2)
                col+=1
            cofactor.append(co_line)
            col=0
            row+=1
        return Matrix(cofactor)

    def transpose(self):
        size=len(self.matrix)
        transpose=[]
        for col in range(0,size):
            tran_line=[]
            for row in range(0,size):
                tran_line.append(self.matrix[row][col])
            transpose.append(tran_line)
        return Matrix(transpose)

    def dividedby(self,num):
        size=len(self.matrix)
        inverse=[]
        for row in range(0,size):
            inver_line=[]
            for col in range(0,size):
                tmp=self.matrix[row][col]/num
                inver_line.append(tmp)
            inverse.append(inver_line)
        return Matrix(inverse)

    def matrix_multiply(self,inverse):
        size=len(self.matrix)
        
        mul=[]
        tmp=0
        for r_m in range(0,size):
            mul_line=[]
            for c_i in range(0,size):
                for s in range(0,size):
                    tmp+=self.matrix[r_m][s]*inverse.matrix[s][c_i]
                mul_line.append(round(tmp,5))
                tmp=0
            mul.append(mul_line)
        return Matrix(mul)

    def print_all_elements(self):
        for row in self.matrix:
            tmp=[]
            for i in row:
                if(i==0):
                    i=0.0
                tmp2=str(round(i,1))
                tmp.append(tmp2)
            tmp='  '.join(tmp)
            print(tmp)

matrix_list=get_matrix_list("matrix.txt")

cnt=1
for tmp_list in matrix_list:
    tmp_list=Matrix(tmp_list)

    if tmp_list.determinant()==0:
        print(f"Matrix {cnt}")
        print("Determinant is zero. No inverse Matrix\n")
        cnt+=1

    else:
        print(f"Matrix {cnt}")
        tmp_list.print_all_elements()

        co_list=tmp_list.cofactor_matrix()
        co_list=co_list.transpose()
        inv=co_list.dividedby(tmp_list.determinant())
        print("Its inverse is")
        inv.print_all_elements()

        identity=tmp_list.matrix_multiply(inv)
        print("Two matrix multiplication is")
        identity.print_all_elements()
        print("\n")
        cnt+=1

> 추가 첨부파일

코드에서 쓰인 matrix.txt이다.
https://drive.google.com/file/d/1JLUOxh2kDORHDAQia14FZKoJuk5D6LF-/view?usp=share_link
총 29개의 행렬로 구성되어 있다. 자신이 실험해보고 싶은 행렬이 있다면 문서에 형식에 맞게 작성해보자.