• 다음 내용은 [CS-188] Introduction to Aritificial Intelligence, UC Berkeley, Fall 2018의 Readings-Note2을 정리하였음을 밝힙니다.
• 스스로 이해하기에 영문 용어가 이해하기 직관적이면 그대로 사용했습니다.

Summary

• CSP(constraint satisfaction problems)는 일반적으로 NP-hard 문제로 다항식 시간(polynomial time) 안에 효과적으로 풀이 가능한 알고리즘이 존재하지 않는다. 하지만 다음과 같은 휴리스틱을 통해 solution을 찾는 데 효과적으로 시간을 줄일 수 있다.

1. Filtering: 불필요한 백트래킹을 원천적으로 방지하는 필터링 휴리스틱은 forward checking과 arc consistency를 활용해 "할당되지 않을" 변수를 도메인에서 제거한다.
2. Ordering: filtering과 함께 어떤 변수 또는 값을 고를지 기준을 준다. MRV 정책, LCV 정책을 통해 변수를 고른다.
3. Structure: divide and conquer. CSP 문제가 트리 또는 유사 트리라면 분리 가능한 여러 트리로 만들어 각각 문제를 푼다.

CSP

CSP는 planning problem인 탐색 문제와 달리 identification 유형의 문제를 가리킨다.
"어떻게 목적지에 도착하는지" 경로를 풀어야 하는 탐색 문제와 달리 CSP는 "지금 목적지인지 아닌지" 즉 문제를 풀 수 있는지 그 여부만 확인한다.

1. 변수: 총 N개의 변수 $X_1, ..., X_N$
2. 도메인: 각 변수 $X$는 d개의 도메인 값 $x_1, ..., x_d$을 가질 수 있다.
3. 제약조건: 변수가 가질 수 있는 값에 제한이 있다. "다른 변수가 가진 값"과 같이 고려해야 하는 경우도 있다.

• CSP 중 N-queens라는 문제가 있다. NxN 체스판 위에 N개의 퀸을 놓아야 한다. 이때 서로 공격하지 않는 상황을 구하는 문제다.

1. 변수: 체스판 위 퀸이 놓일 수 있는 공간 $X_{ij}$으로 총 NxN개
2. 도메인: 각 좌표 $X_{ij}$ 위에 퀸이 있는지 없는지 확인하는 값 {0, 1} (또는 {true, false})
3. 제약조건: 같은 행, 같은 행, 같은 대각선 방향(major, minor)으로 두 개 이상의 퀸이 놓이면 안 된다. 체스판 위에 총 N개의 퀸이 있어야 한다.

brute-force로 N-queens를 풀기 위한 시간 복잡도는 $O(d^N)=O(2^{N^2})$이다. 시간복잡도를 줄여 충분히 풀 만한 시간 내에 해결책을 찾으려면 어떻게 해야 할까?
그 이전에, CSP를 어떻게 문제로 옮기는지 살펴보자.

• map-coloring 역시 유명한 CSP 문제이다. 페인트 종류가 한정되어 있을 때, 주어진 지도에서 인접한 지역의 색깔은 다르게 칠할 수 있는 경우를 구한다.

1. 변수: 주어진 지도의 지역 수 N
2. 도메인: 각 지역이 칠해질 수 있는 페인트 수 d
3. 제약조건: 인접한 지역들은 같은 페인트로 칠해지면 안 된다.

이 경우 CSP를 풀기 쉽게 그래프로 옮겨놓을 수 있다. 이른바 제약조건 그래프(constraint graphs)이다.

1. Constraint Graphs

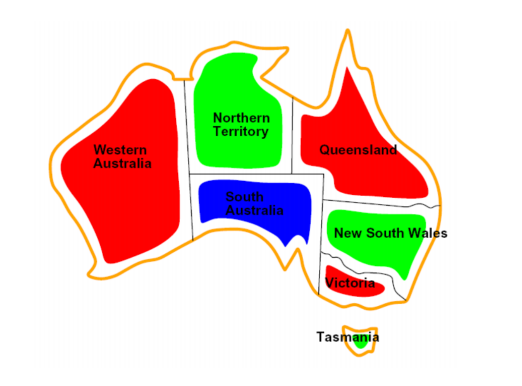
위 지도에서 변수는 7개, 도메인은 3개이다. 제약조건의 인접성을 표시하기 위해 그래프에서 노드 사이의 간선으로 표시할 수 있다.

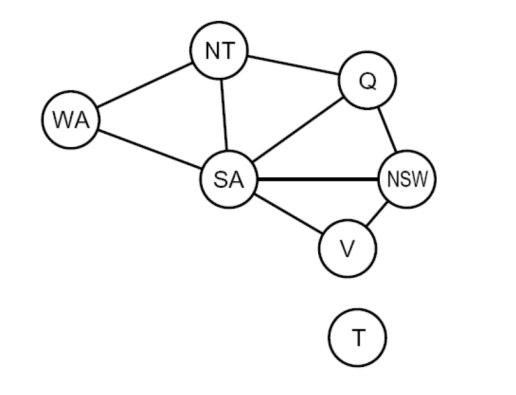
2. CSP solver

백트래킹 알고리즘을 통해 위 CSP 그래프를 풀어보자. CSP를 풀기 위해서는,

1. 변수에 값을 할당할 때 기존의 다른 변수가 지닌 값과 충돌(conflict)한다면 고르지 않는다.
2. 변수를 정렬한 순서를 고정한 뒤에 값을 할당하자.

• 백트래킹 알고리즘은 특정 값을 할당한 노드 → 다음 노드의 값 할당... → 마지막 노드 값 할당으로 이어져 모든 노드에 값을 할당할 때까지 구현되는 까닭에 DFS의 일종이다.
• 위 구현 방식은 인접 지역이 이미 공통된 색으로 칠해진 이후에도 모든 지도를 칠한 뒤에 성공 여부를 판단하는 DFS에 비해 백트래킹 알고리즘은 제약조건을 침범하지 않는 값을 할당한다.

brute force DFS에 비해 백트래킹 알고리즘은 더 적은 경우의 수를 고려하기 때문에 더 좋은 알고리즘이다.
하지만 변수 당 도메인 범위를 판단하는 filtering, 제약 조건과 충돌하는 수를 기준으로 변수 및 값을 고르는 ordering, 트리 하부 구조로 나눠 연산하는 structure 등 휴리스틱을 사용한다면 더 빨리 solution을 얻을 수 있다.