• 다음 내용은 [CS-188] Introduction to Aritificial Intelligence, UC Berkeley, Fall 2018의 Readings-Note2을 정리하였음을 밝힙니다.
• 스스로 이해하기에 영문 용어가 이해하기 직관적이면 그대로 사용했습니다.

Filtering

필터링은 이후 백트래킹될 값을 사전에 제거함으로써 아직 할당되지 않은 변수 도메인을 프루닝(pruning)하는 방법이다. forward checking과 arc consistency를 통해 손쉬운 필터링이 가능하다.

1. Forward Checking

값이 변수 $X_i$에 할당될 때마다 이 변수 $X_i$와 인접한 다른 변수들의 값 도메인 중 제약조건과 충돌하는 경우를 미리 프루닝한다.

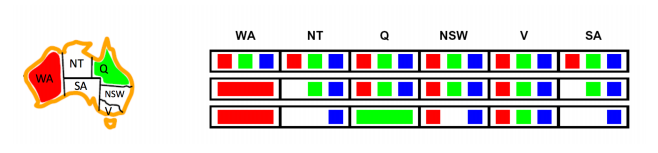
위 map-coloring의 initialization 0단계에서는 6개 변수 도메인 모두 3개의 색을 칠할 수 있다. 하지만 1단계로 WA에서 빨간색을 할당하자 forward checking을 통해 WA와 인접한 NT, SA 변수가 가지고 있는 도메인 내 값들을 확인한다. 이때 WA가 가진 빨간색과 "같은" (즉 제약조건에 충돌을 일으키는) 빨간색이 NT, SA의 도메인에서 사라진다.

2. Arc Cosnsitency

forward checking을 통해 일반화할 수 있는 원칙으로 도메인 값이 제거된 변수와 맞닿아 있는 다른 변수 또한 도메인 값을 다시 한 번 확인하는 규칙이다.

위 상황에서는 WA에 빨간색, Q에 초록색을 할당한 상황이다. 즉 각 지역에 값을 할당할 때 인접한 NT, SA, NSW 등 변수의 도메인에서 제약조건과 충돌을 일으키는 값이 제거되었다.

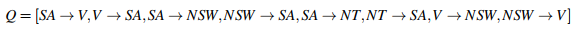
arc consistency 확인을 큐에 넣어둔 인접한 지역들을 활용하자. 만일 특정 두 지역이 인접했을 때에는, 위 문제에서 방향이 없으므로 양방향으로 arc를 표현할 수 있다.

이때 FIFO의 큐에서 가장 앞의 SA → V를 꺼내자. tail 노드인 SA의 도메인은 파란색 하나 뿐이고, head 노드 V의 도메인은 가득 차 있다. 이때 tail이 가지고 있는 파란색을 head가 가지고 있는 도메인에서 제거했을 때 도메인의 값이 남아 있는지 확인한다! 즉 V 도메인은 빨간색과 초록색이 남아 있을 수 있기 때문에 그대로 넘어간다.

하지만 V → SA를 꺼냈을 때에는 달라진다. V의 도메인 중 파란색을 살펴보고 head 노드인 SA에서 동일한 색깔인 파란색을 제거한다고 가정해보자. 그러면 SA 도메인은 텅 비어버리기 때문에 arc consistency가 깨진다. 이 시점에서 V의 도메인에서 파란색을 프루닝한다.

V 도메인의 값이 프루닝된 시점에서 다시 V가 head인 모든 경우를 다시 큐에 집어넣어야 한다. V가 head인 경우는 SA → V, NSW → V가 있다. 큐에 없는 경우만 다시 집어넣자.

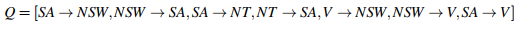
이 과정에서 계속해서 큐를 통해 arc consistency를 확인하며 도메인이 변경된 변수와 연결된 arc가 계속 들어온다.

하지만 위 경우처럼 arc consisntecy를 유지하기 위해서 계속해서 큐에 enqueue/dequeue가 반복되더라도 도메인이 빌 수밖에 없는 순간이 있다. 즉 백트래킹이 일어나는 때다.

3. AC-3 algorithm

위 과정을 알고리즘으로 옮긴 AC-3 알고리즘을 통해 필터링을 할 수 있다.

• time complexiy: $O(ed^3)$으로 arc의 수 e와 가장 큰 도메인의 크기 d. arc consistency를 확인하기 위해 arch 별로 (e) 도메인을 확인한다.
• trade-off: forward checking보다 도메인 프루닝이 빠르기 때문에 백트래킹이 드물지만 연산이 더 많이 요구된다.

forward checking과 arc consistency 중 어떤 방법을 필터링 기법으로 활용하는지는 trade-off를 보고 선택해야 한다.

Ordering

CSP를 풀 때 어떤 순서대로 변수를, 값을 고를지 미리 기준을 세워야 한다. 이때 랜덤 또는 알파벳 기준으로 고르는 것보다 효과적인 방법이 존재한다.

1. MRV

• 변수 할당 시 가장 제약 조건이 많은 변수를 고른다.

제약 조건이 많다는 뜻은 곧 할당될 값으로 계속 작동할 가능성이 높다는 뜻이며, 만일 고르지 않은 채로 남길 경우 백트래킹으로 이어진다는 뜻이다. 그래서 만일 이후에 골라 백트래킹을 해야 한다 할지라도, 빨리 백트래킹을 하는 게 시간적으로 효율적이다.

2. LCV

• 값 할당 시 가장 선택지가 많은 값을 고른다.

변수에서 가장 좁은 길을 골랐다면 값은 가장 넓은 길을 고르자. 이때 아직 할당받지 못한 나머지 도메인에서 가장 적은 수만을 프루닝할 수 있다.

MRV와 LCV는 일종의 수학적 원칙이라기보다도 백트래킹이 "가장 드물게" 일어날 법한 실용적인 경우로 연산을 이어준다. 또는 백트래킹이 일어났다 할지라도 최대한 빨리 다음 연산으로 넘어갈 수 있도록(MRV) 도와준다.